
(1) 单位矩阵
即主对角线上的元素均为1,其余元素均为0的正方形矩阵。
在NumPy中可以用eye函数创建一个这样的二维数组,我们只需要给定一个参数,用于指定矩阵中1的元素个数。
例如,创建3×3的数组:
import numpy as np I2 = np.eye(3) print(I2) [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
(2) 使用savetxt函数将数据存储到文件中,当然我们需要指定文件名以及要保存的数组。
np.savetxt('eye.txt', I2)#创建一个eye.txt文件,用于保存I2的数据
CSV(Comma-Separated Value,逗号分隔值)格式是一种常见的文件格式;通常,数据库的转存文件就是CSV格式的,文件中的各个字段对应于数据库表中的列;电子表格软件(如Microsoft Excel)可以处理CSV文件。
note: ,NumPy中的loadtxt函数可以方便地读取CSV文件,自动切分字段,并将数据载入NumPy数组
data.csv的数据内容:
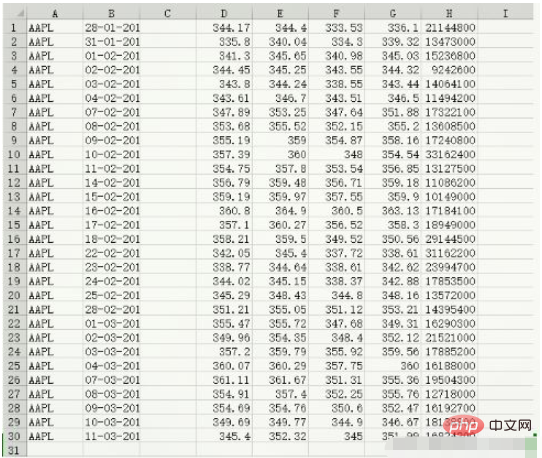
c, v = np.loadtxt('data.csv', delimiter=',', usecols=(6,7), unpack=True) # usecols的参数为一个元组,以获取第7字段至第8字段的数据 # unpack参数设置为True,意思是分拆存储不同列的数据,即分别将收盘价和成交量的数组赋值给变量c和v print(c) [336.1 339.32 345.03 344.32 343.44 346.5 351.88 355.2 358.16 354.54 356.85 359.18 359.9 363.13 358.3 350.56 338.61 342.62 342.88 348.16 353.21 349.31 352.12 359.56 360. 355.36 355.76 352.47 346.67 351.99] print(v) [21144800. 13473000. 15236800. 9242600. 14064100. 11494200. 17322100. 13608500. 17240800. 33162400. 13127500. 11086200. 10149000. 17184100. 18949000. 29144500. 31162200. 23994700. 17853500. 13572000. 14395400. 16290300. 21521000. 17885200. 16188000. 19504300. 12718000. 16192700. 18138800. 16824200.] print(type(c)) print(type(v))
VWAP概述:VWAP(Volume-Weighted Average Price,成交量加权平均价格)是一个非常重要的经济学量,它代表着金融资产的“平均”价格。
某个价格的成交量越高,该价格所占的权重就越大。
VWAP就是以成交量为权重计算出来的加权平均值,常用于算法交易。
vwap = np.average(c,weights=v) print('成交量加权平均价格vwap =', vwap) 成交量加权平均价格vwap = 350.5895493532009
NumPy中的mean函数可以计算数组元素的算术平均值
print('c数组中元素的算数平均值为: {}'.format(np.mean(c))) c数组中元素的算数平均值为: 351.0376666666667
TWAP概述:
在经济学中,TWAP(Time-Weighted Average Price,时间加权平均价格)是另一种“平均”价格的指标。既然我们已经计算了VWAP,那也来计算一下TWAP吧。其实TWAP只是一个变种而已,基本的思想就是最近的价格重要性大一些,所以我们应该对近期的价格给以较高的权重。最简单的方法就是用arange函数创建一个从0开始依次增长的自然数序列,自然数的个数即为收盘价的个数。当然,这并不一定是正确的计算TWAP的方式。
t = np.arange(len(c)) print('时间加权平均价格twap=', np.average(c, weights=t)) 时间加权平均价格twap= 352.4283218390804
h, l = np.loadtxt('data.csv', delimiter=',', usecols=(4,5), unpack=True) print('h数据为: \n{}'.format(h)) print('-'*10) print('l数据为: \n{}'.format(l)) h数据为: [344.4 340.04 345.65 345.25 344.24 346.7 353.25 355.52 359. 360. 357.8 359.48 359.97 364.9 360.27 359.5 345.4 344.64 345.15 348.43 355.05 355.72 354.35 359.79 360.29 361.67 357.4 354.76 349.77 352.32] ---------- l数据为: [333.53 334.3 340.98 343.55 338.55 343.51 347.64 352.15 354.87 348. 353.54 356.71 357.55 360.5 356.52 349.52 337.72 338.61 338.37 344.8 351.12 347.68 348.4 355.92 357.75 351.31 352.25 350.6 344.9 345. ] print('h数据的最大值为: {}'.format(np.max(h))) print('l数据的最小值为: {}'.format(np.min(l))) h数据的最大值为: 364.9 l数据的最小值为: 333.53 NumPy中有一个ptp函数可以计算数组的取值范围 该函数返回的是数组元素的最大值和最小值之间的差值 也就是说,返回值等于max(array) - min(array) print('h数据的最大值-最小值的差值为: \n{}'.format(np.ptp(h))) print('l数据的最大值-最小值的差值为: \n{}'.format(np.ptp(l))) h数据的最大值-最小值的差值为: 24.859999999999957 l数据的最大值-最小值的差值为: 26.970000000000027
中位数:我们可以用一些阈值来除去异常值,但其实有更好的方法,那就是中位数。
将各个变量值按大小顺序排列起来,形成一个数列,居于数列中间位置的那个数即为中位数。
例如,我们有1、2、3、4、5这5个数值,那么中位数就是中间的数字3。
m = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True) print('m数据中的中位数为: {}'.format(np.median(m))) m数据中的中位数为: 352.055 # 数组排序后,查找中位数 sorted_m = np.msort(m) print('m数据排序: \n{}'.format(sorted_m)) N = len(c) print('m数据中的中位数为: {}'.format((sorted_m[N//2]+sorted_m[(N-1)//2])/2)) m数据排序: [336.1 338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5 346.67 348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21 354.54 355.2 355.36 355.76 356.85 358.16 358.3 359.18 359.56 359.9 360. 363.13] m数据中的中位数为: 352.055 方差: 方差是指各个数据与所有数据算术平均数的离差平方和除以数据个数所得到的值。 print('variance =', np.var(m)) variance = 50.126517888888884 var_hand = np.mean((m-m.mean())**2) print('var =', var_hand) var = 50.126517888888884
注意:样本方差和总体方差在计算上的区别。总体方差是用数据个数去除离差平方和,而样本方差则是用样本数据个数减1去除离差平方和,其中样本数据个数减1(即n-1)称为自由度。之所以有这样的差别,是为了保证样本方差是一个无偏估计量。
在学术文献中,收盘价的分析常常是基于股票收益率和对数收益率的。
简单收益率是指相邻两个价格之间的变化率,而对数收益率是指所有价格取对数后两两之间的差值。
我们在高中学习过对数的知识,“a”的对数减去“b”的对数就等于“a除以b”的对数。因此,对数收益率也可以用来衡量价格的变化率。
注意,由于收益率是一个比值,例如我们用美元除以美元(也可以是其他货币单位),因此它是无量纲的。
总之,投资者最感兴趣的是收益率的方差或标准差,因为这代表着投资风险的大小。
(1) 首先,我们来计算简单收益率。NumPy中的diff函数可以返回一个由相邻数组元素的差值构成的数组。这有点类似于微积分中的微分。为了计算收益率,我们还需要用差值除以前一天的价格。不过这里要注意,diff返回的数组比收盘价数组少一个元素。returns = np.diff(arr)/arr[:-1]
注意,我们没有用收盘价数组中的最后一个值做除数。接下来,用std函数计算标准差:
print ("Standard deviation =", np.std(returns))
(2) 对数收益率计算起来甚至更简单一些。我们先用log函数得到每一个收盘价的对数,再对结果使用diff函数即可。
logreturns = np.diff( np.log(c) )
一般情况下,我们应检查输入数组以确保其不含有零和负数。否则,将得到一个错误提示。不过在我们的例子中,股价总为正值,所以可以将检查省略掉。
(3) 我们很可能对哪些交易日的收益率为正值非常感兴趣。
在完成了前面的步骤之后,我们只需要用where函数就可以做到这一点。where函数可以根据指定的条件返回所有满足条件的数组元素的索引值。
输入如下代码:
posretindices = np.where(returns > 0) print "Indices with positive returns", posretindices 即可输出该数组中所有正值元素的索引。 Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)
(4) 在投资学中,波动率(volatility)是对价格变动的一种度量。历史波动率可以根据历史价格数据计算得出。计算历史波动率(如年波动率或月波动率)时,需要用到对数收益率。年波动率等于对数收益率的标准差除以其均值,再除以交易日倒数的平方根,通常交易日取252天。用std和mean函数来计算
代码如下所示:
annual_volatility = np.std(logreturns)/np.mean(logreturns) annual_volatility = annual_volatility / np.sqrt(1./252.)
(5) sqrt函数中的除法运算。在Python中,整数的除法和浮点数的除法运算机制不同(python3已修改该功能),我们必须使用浮点数才能得到正确的结果。与计算年波动率的方法类似,计算月波动率如下:
annual_volatility * np.sqrt(1./12.) c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True) returns = np.diff(c)/c[:-1] print('returns的标准差: {}'.format(np.std(returns))) logreturns = np.diff(np.log(c)) posretindices = np.where(returns>0) print('retruns中元素为正数的位置: \n{}'.format(posretindices)) annual_volatility = np.std(logreturns)/np.mean(logreturns) annual_volatility = annual_volatility/np.sqrt(1/252) print('每年波动率: {}'.format(annual_volatility)) print('每月波动率:{}'.format(annual_volatility*np.sqrt(1/12))) returns的标准差: 0.012922134436826306 retruns中元素为正数的位置: (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28], dtype=int64),) 每年波动率: 129.27478991115132 每月波动率:37.318417377317765
Atas ialah kandungan terperinci Python常用函数中的NumPy怎么使用. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




