Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java-javaTutorial-php.cn

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

PHPz

Lepaskan： 2023-04-25 16:40:08

ke hadapan

1523 orang telah melayarinya

①Konsep

Pokok carian binari juga dipanggil pokok pengisihan binari Ia sama ada pokok kosong** atau mempunyai ciri-ciri berikut Pokok binari:

Jika subpokok kirinya tidak kosong, maka nilai semua nod pada subpokok kiri adalah kurang daripada nilai nod akar

Jika subpokok kanannya tidak kosong, maka nilainya Semua nod pada subpokok kanan adalah lebih besar daripada nilai nod akar

Subpokok kiri dan kanannya juga merupakan pokok carian binari

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

. ② Operasi - Carian

dalam pepohon carian binari adalah serupa dengan carian binari untuk

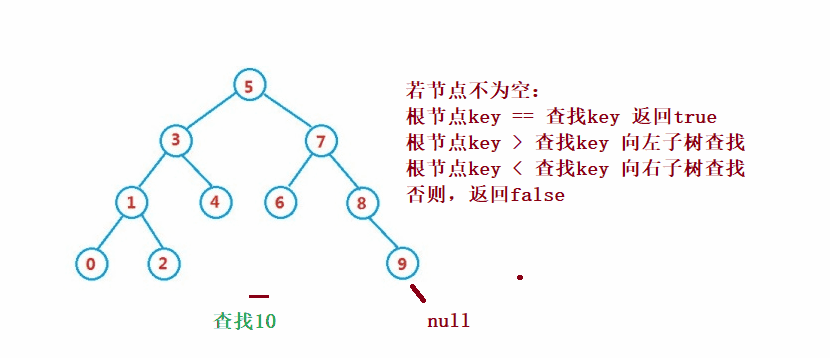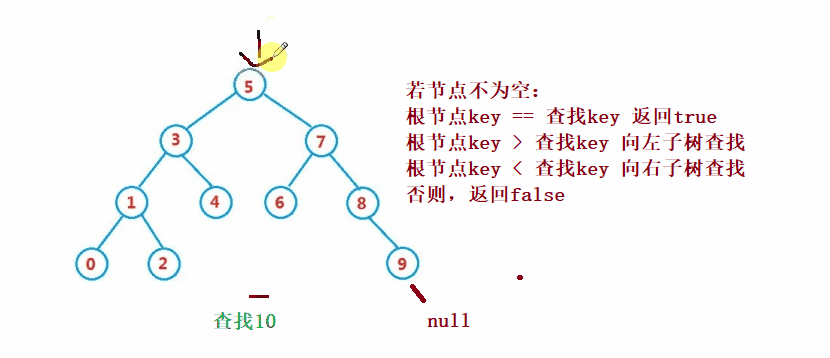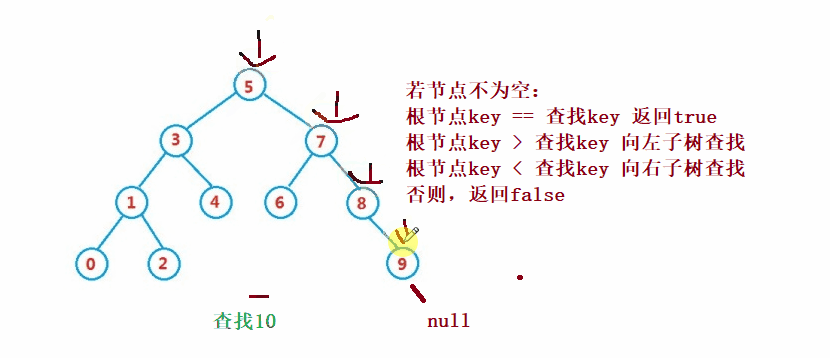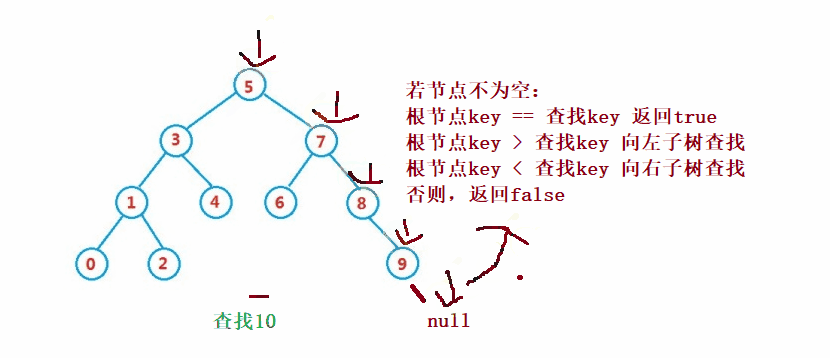
Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

Salin selepas log masuk

③Operasi-Sisip

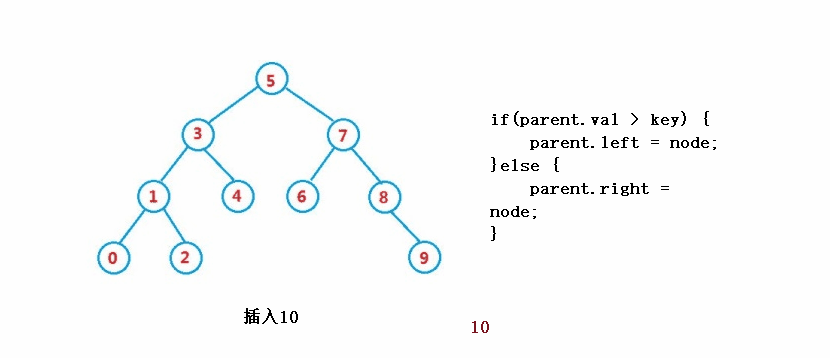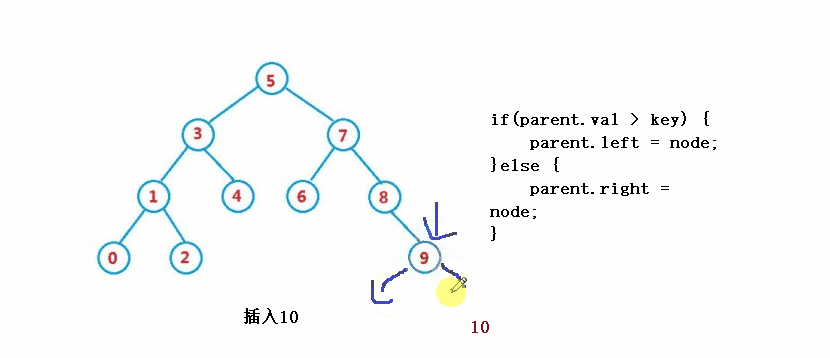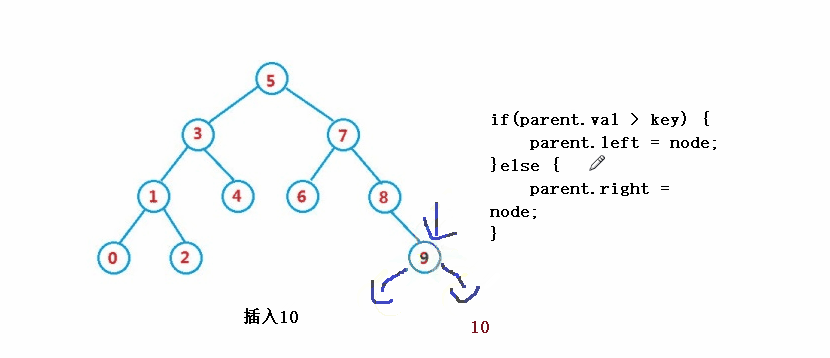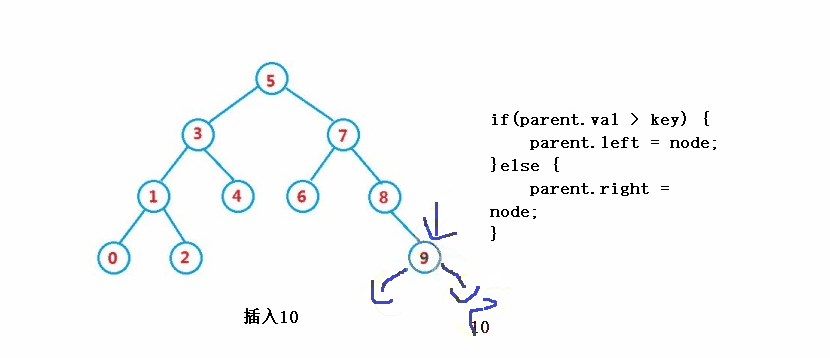Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java <🎜 . nod induk bagi nod yang akan dipadamkan ialah induk

  public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }

Salin selepas log masuk

1 cur.left == null

1, kemudian root = cur.right

2 . cur bukan akar, cur ialah induk.kiri, Kemudian induk.kiri = cur.kanan

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java 2

1. cur ialah akar, kemudian akar = cur .kiri

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java 2. cur ialah induk.kiri, kemudian induk.kiri = cur.kiri

3. cur bukan akar, cur ialah parent.right, kemudian parent.right = cur.left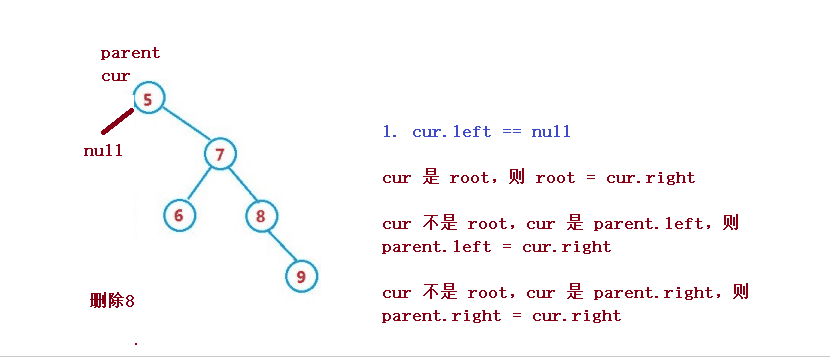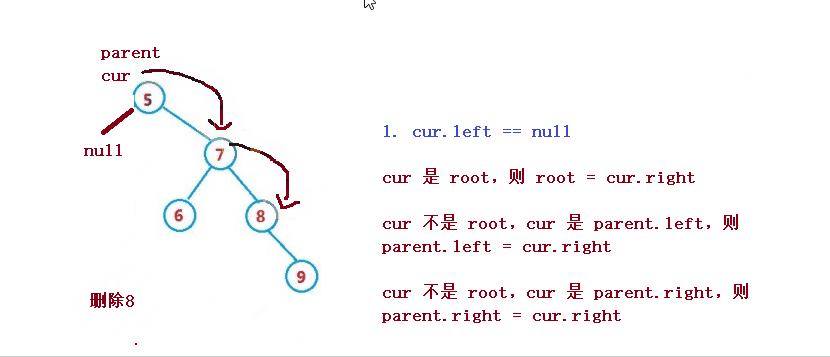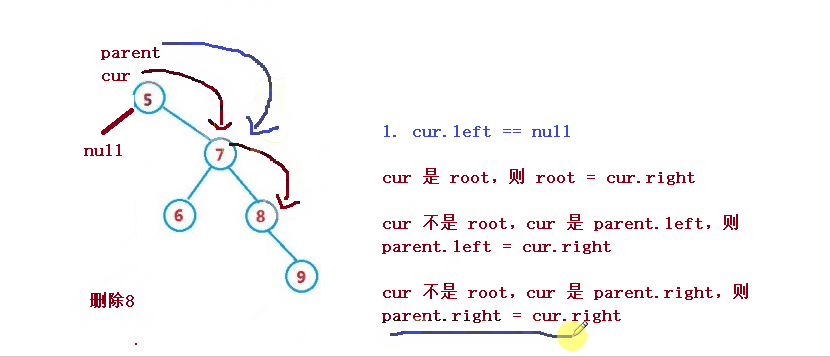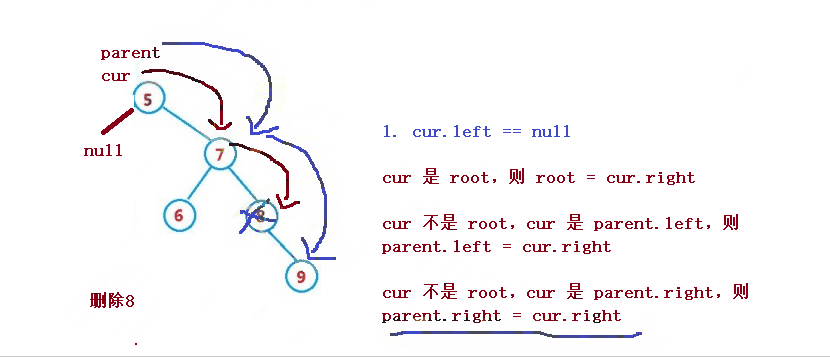 Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

Kes kedua adalah sama dengan kes pertama, kecuali dalam arah yang bertentangan Tiada lagi lukisan di sini

3. cur.left != null && cur.right != null

perlu dipadam menggunakan kaedah penggantian, iaitu mencari nod pertama dalam susunan tengah (dengan terkecil kod kunci) dalam subpokok kanannya, mengisinya dengan nilainya ke dalam nod yang dipadam, dan kemudian memprosesnya Masalah memadamkan nod ini

Apabila kita memadamkan nod apabila kedua-dua subpokok kiri dan kanan tidak kosong, memadamkan nod akan memusnahkan struktur pokok, jadi kami menggunakan kaedah kambing hitam untuk menyelesaikannya Proses pemadaman sebenar masih Dalam dua kes di atas, sifat mencari pokok binari masih digunakan di sini

<. 🎜>

⑤ Analisis prestasi Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

Kedua-dua operasi sisipan dan pemadaman mesti dicari terlebih dahulu kecekapan mewakili prestasi setiap operasi dalam pepohon carian binari.

Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java Untuk pepohon carian binari dengan n nod, jika kebarangkalian mencari setiap elemen adalah sama, purata panjang carian bagi pepohon carian binari ialah fungsi kedalaman nod dalam pepohon carian binari, iaitu nod Semakin dalam titik, semakin banyak perbandingan dibuat.

Tetapi untuk set kod kunci yang sama, jika susunan pemasukan setiap kod kunci berbeza, pepohon carian binari dengan struktur berbeza boleh diperolehi: Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java

Dalam kes optimum, binari pokok carian selesai Untuk pokok binari, purata bilangan perbandingan ialah:

public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
  public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

Salin selepas log masuk

Dalam kes yang paling teruk, pokok carian binari merosot menjadi pokok cawangan tunggal, dan purata bilangan perbandingan ialah:

⑥完整代码

public class TextDemo {
 
    public static class Node {
        public int val;
        public Node left;
        public Node right;
 
        public Node (int val) {
            this.val = val;
        }
    }
 
 
    public Node root;
 
    /**
     * 查找
     * @param key
     */
    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }
 
    /**
     *
     * @param key
     * @return
     */
    public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }
 
    public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
    public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
 
}

Salin selepas log masuk

Atas ialah kandungan terperinci Penjelasan terperinci tentang contoh menambah, memasukkan, memadam dan mencipta pepohon carian binari Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!