
Penormalan data ialah langkah yang sangat kritikal dalam prapemprosesan data pembelajaran mendalam, yang boleh menyatukan dimensi dan menghalang data kecil daripada ditelan.
Normalization adalah untuk menukar semua data kepada [0,1] atau [-1,1] Tujuannya adalah untuk membatalkan pesanan perbezaan magnitud antara setiap dimensi data dan mengelakkan ralat ramalan rangkaian yang berlebihan disebabkan oleh susunan perbezaan magnitud yang besar dalam data input dan output.
Untuk kemudahan pemprosesan data seterusnya, normalisasi boleh mengelakkan beberapa masalah berangka yang tidak perlu.
Untuk penumpuan yang lebih pantas apabila program dijalankan
Satukan dimensi. Kriteria penilaian untuk data sampel adalah berbeza, jadi ia perlu didimensi dan kriteria penilaian disatukan Ini dianggap sebagai keperluan di peringkat permohonan.
Elakkan ketepuan neuron. Maksudnya, apabila pengaktifan neuron hampir kepada 0 atau 1, di kawasan ini, kecerunannya hampir 0, supaya semasa proses perambatan belakang, kecerunan tempatan akan hampir kepada 0, yang sangat tidak menguntungkan untuk rangkaian. latihan.
Pastikan nilai kecil dalam data output tidak ditelan.
Penormalan linear juga dipanggil minimum- Normalisasi diskret, ialah transformasi linear data asal, memetakan nilai data antara [0,1]. Dinyatakan sebagai formula:
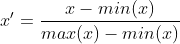
Penyawaian perbezaan mengekalkan perhubungan yang wujud dalam data asal dan merupakan kaedah paling mudah untuk menghapuskan pengaruh dimensi dan julat nilai data. Kod tersebut dilaksanakan seperti berikut:
def MaxMinNormalization(x,Max,Min):
x = (x - Min) / (Max - Min);
return xSkop aplikasi: lebih sesuai untuk situasi di mana nilai berangka secara relatif tertumpu
Kelemahan:
Jika max dan min tidak stabil , adalah mudah untuk membuat keputusan normal tidak stabil, menjadikan kesan penggunaan seterusnya tidak stabil. Jika julat nilai melebihi atribut semasa [min, maks], ia akan menyebabkan sistem melaporkan ralat. Min dan maks perlu ditentukan semula.
Jika nilai dalam set nilai adalah sangat besar, maka nilai normal akan menghampiri 0 dan tidak akan banyak berbeza. (seperti 1,1.2,1.3,1.4,1.5,1.6,10) set data ini.
Penormalan skor Z juga dipanggil normalisasi sisihan piawai, min bagi data yang diproses ialah 0 dan sisihan piawai ialah 1. Formula penukaran ialah:
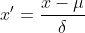
di mana 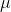 ialah min bagi data asal dan
ialah min bagi data asal dan 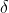 ialah sisihan piawai bagi data asal menggunakan formula standardisasi
ialah sisihan piawai bagi data asal menggunakan formula standardisasi
Kaedah ini memberikan min dan sisihan piawai bagi data asal untuk menyeragamkan data. Data yang diproses mematuhi taburan normal piawai, iaitu min ialah 0 dan sisihan piawai ialah 1. Kuncinya di sini ialah taburan normal piawai komposit
Kod tersebut dilaksanakan seperti berikut:
def Z_ScoreNormalization(x,mu,sigma):
x = (x - mu) / sigma;
return xKaedah ini memetakan nilai atribut kepada antara [-1,1] dengan mengalihkan tempat perpuluhan nilai atribut Bilangan tempat perpuluhan yang dialihkan bergantung pada maksimum nilai mutlak nilai atribut. Formula penukaran ialah:
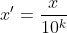
Kaedah ini termasuk log, eksponen, tangen
Skop aplikasi: selalunya Ia digunakan dalam senario di mana analisis data agak besar Sesetengah nilai sangat besar dan ada yang sangat kecil.
Dalam latihan rangkaian saraf yang lalu, hanya data lapisan input dinormalkan Tetapi tiada pemprosesan penormalan masuk lapisan tengah. Walaupun kami telah menormalkan data input, selepas data input telah mengalami pendaraban matriks seperti 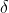 , pengedaran datanya berkemungkinan besar berubah dan apabila bilangan lapisan rangkaian terus bertambah. Pengedaran data akan semakin berubah. Oleh itu, proses normalisasi di lapisan tengah rangkaian saraf ini, yang menjadikan kesan latihan lebih baik, dipanggil normalisasi kelompok (BN)
, pengedaran datanya berkemungkinan besar berubah dan apabila bilangan lapisan rangkaian terus bertambah. Pengedaran data akan semakin berubah. Oleh itu, proses normalisasi di lapisan tengah rangkaian saraf ini, yang menjadikan kesan latihan lebih baik, dipanggil normalisasi kelompok (BN)
Mengurangkan pemilihan parameter buatan
Mengurangkan keperluan untuk kadar pembelajaran, kita boleh menggunakan kadar pembelajaran yang besar dalam keadaan awal atau menggunakan kadar pembelajaran yang lebih kecil, algoritma juga boleh cepat berlatih untuk berkumpul.
Menggantikan pengedaran data asal, yang mengurangkan overfitting pada tahap tertentu (menghalang sampel tertentu daripada kerap dipilih dalam setiap kumpulan latihan)
Kurangkan kehilangan kecerunan, mempercepatkan penumpuan dan meningkatkan ketepatan latihan.
Input: Hasil keluaran lapisan sebelumnya X={x1,x2,...xm} , Pembelajaran parameter 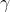 ,
, 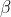
Proses algoritma:
1) Kira min data keluaran lapisan sebelumnya:
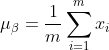
Di mana, m ialah saiz kumpulan sampel latihan ini.
2) Kira sisihan piawai data output lapisan sebelumnya:
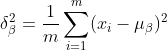
3) Pemprosesan normalisasi menghasilkan
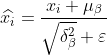
 dalam formula ialah nilai kecil yang hampir dengan 0 yang ditambah untuk mengelakkan penyebut menjadi 0.
dalam formula ialah nilai kecil yang hampir dengan 0 yang ditambah untuk mengelakkan penyebut menjadi 0.
4) Pembinaan semula, bina semula data yang diperoleh selepas proses normalisasi di atas, dan dapatkan:
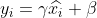
di mana 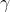 ,
, 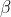 ialah parameter yang boleh dipelajari.
ialah parameter yang boleh dipelajari.
Atas ialah kandungan terperinci Apakah kaedah normalisasi biasa dalam Python?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




