Pepohon regresi tulisan tangan dari awal menggunakan Python-Tutorial Python-php.cn

Demi kesederhanaan, rekursi akan digunakan untuk mencipta nod pokok Walaupun rekursi bukanlah pelaksanaan yang sempurna, ia adalah yang paling intuitif untuk menerangkan prinsip.

Mula-mula import perpustakaan

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

Salin selepas log masuk

Mula-mula kita perlu mencipta data latihan, data kita akan mempunyai pembolehubah bebas (x) dan pembolehubah bersandar (y) dan menggunakan numpy dalam nilai bergantung Menambah hingar Gaussian boleh dinyatakan secara matematik sebagai

Pepohon regresi tulisan tangan dari awal menggunakan Python

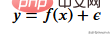
di mana bunyi bising. Kod ditunjukkan di bawah.

def f(x):
mu, sigma = 0, 1.5
return -x**2 + x + 5 + np.random.normal(mu, sigma, 1)
num_points = 300
np.random.seed(1)

x = np.random.uniform(-2, 5, num_points)
y = np.array( [f(i) for i in x] )
plt.scatter(x, y, s = 5)

Salin selepas log masuk

Pepohon regresi tulisan tangan dari awal menggunakan Python

Pokok Regresi

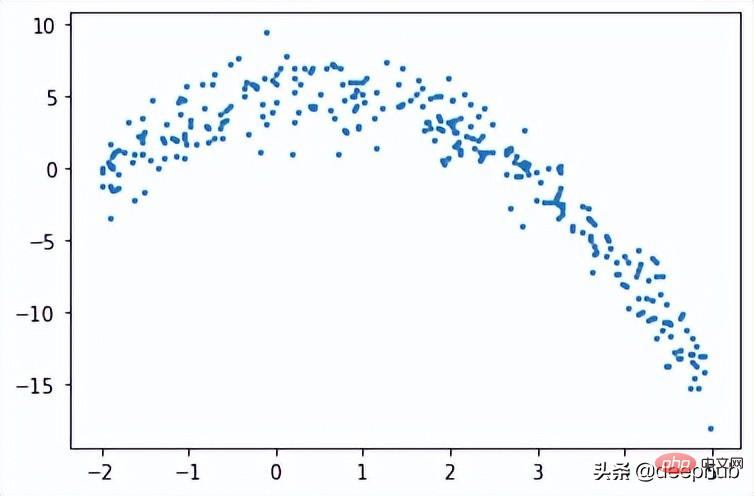
Dalam pepohon regresi, data berangka diramalkan dengan mencipta pepohon berbilang nod. Rajah di bawah menunjukkan contoh struktur pokok bagi pokok regresi, di mana setiap nod mempunyai ambang yang digunakan untuk membahagikan data.

Pepohon regresi tulisan tangan dari awal menggunakan Python

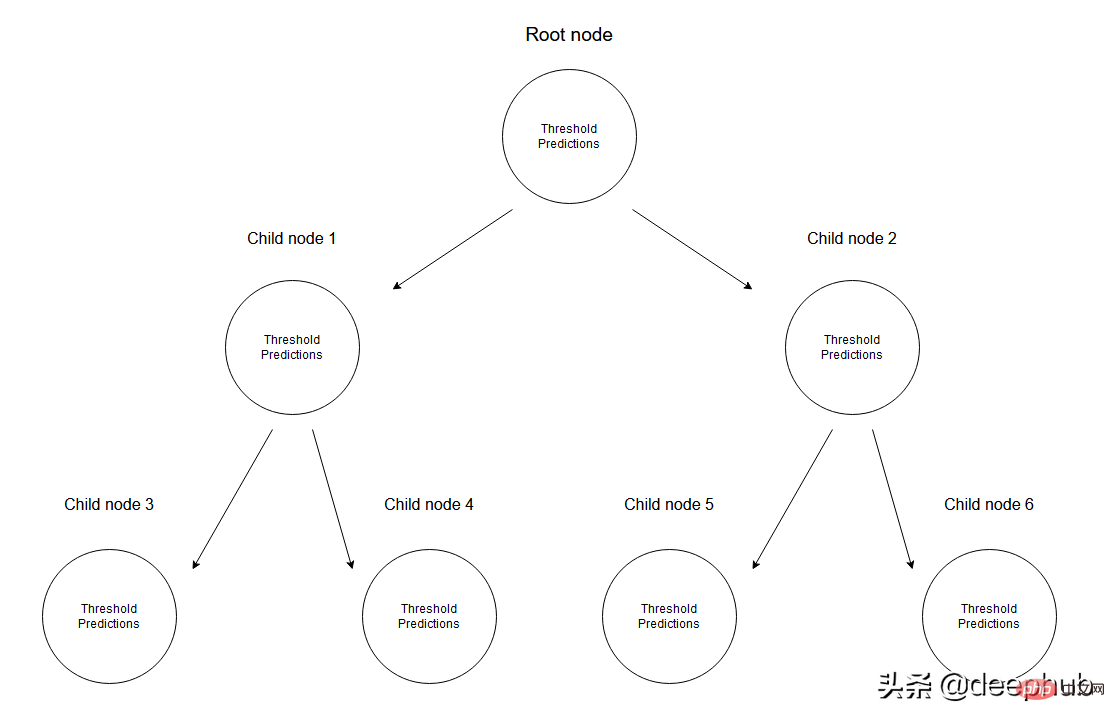
Memandangkan satu set data, nilai input akan mencapai nod daun melalui spesifikasi yang sepadan. Semua nilai input yang mencapai nod M boleh diwakili oleh subset X. Secara matematik, mari kita ungkapkan keadaan ini dari segi fungsi yang memberikan 1 jika nilai input yang diberikan mencapai nod M dan 0 sebaliknya.

Pepohon regresi tulisan tangan dari awal menggunakan Python

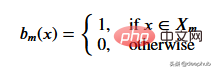
Cari ambang untuk membahagikan data: Ulangi data latihan dengan memilih 2 mata berturut-turut pada setiap langkah dan mengira puratanya. Min yang dikira membahagikan data kepada dua ambang.

Mula-mula mari kita pertimbangkan ambang rawak untuk menunjukkan sebarang situasi tertentu.

threshold = 1.5
low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))
plt.scatter(x, y, s = 5, label = 'Data')
plt.plot([threshold]*2, [-16, 10], 'b--', label = 'Threshold line')
plt.plot([-2, threshold], [low.mean()]*2, 'r--', label = 'Left child prediction line')
plt.plot([threshold, 5], [high.mean()]*2, 'r--', label = 'Right child prediction line')
plt.plot([-2, 5], [y.mean()]*2, 'g--', label = 'Node prediction line')
plt.legend()

Salin selepas log masuk

Pepohon regresi tulisan tangan dari awal menggunakan Python

Garis menegak biru mewakili satu ambang, yang kami anggap ialah min bagi mana-mana dua titik dan akan digunakan untuk membahagikan data kemudian.

Ramalan pertama kami untuk masalah ini ialah purata (garisan mendatar hijau) semua data latihan (paksi-y). Dan dua garis merah adalah ramalan nod anak yang akan dibuat.

Adalah jelas bahawa kedua-dua purata ini tidak mewakili data kami dengan baik, tetapi perbezaannya juga jelas: ramalan nod induk (garis hijau) mendapat min semua data latihan, yang kami bahagikan kepada 2 nod Anak, 2 nod anak ini mempunyai ramalannya sendiri (garis merah). Berbanding dengan garis hijau, kedua-dua nod anak ini lebih baik mewakili data latihan yang sepadan. Pepohon regresi akan terus membahagikan data kepada 2 bahagian - mencipta 2 nod anak daripada setiap nod sehingga nilai hentian tertentu dicapai (iaitu jumlah minimum data yang boleh dimiliki oleh nod). Ia menghentikan proses pembinaan pokok lebih awal, yang kami panggil pokok pra-pangkas.

Mengapa ada mekanisme berhenti awal? Jika kita meneruskan penugasan sehingga nod hanya mempunyai satu nilai, ini mewujudkan senario overfitting di mana setiap data latihan hanya boleh meramalkan dirinya sendiri.

Penjelasan: Apabila model selesai, ia tidak akan menggunakan nod akar atau sebarang nod perantaraan untuk meramalkan sebarang nilai; ia akan menggunakan daun pokok regresi (yang akan menjadi nod terakhir pokok) untuk meramal.

Untuk mendapatkan ambang yang paling mewakili data bagi ambang tertentu, kami menggunakan jumlah baki kuasa dua. Ia boleh ditakrifkan secara matematik sebagai

Pepohon regresi tulisan tangan dari awal menggunakan Python

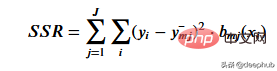
Mari lihat cara langkah ini berfungsi.

Pepohon regresi tulisan tangan dari awal menggunakan Python

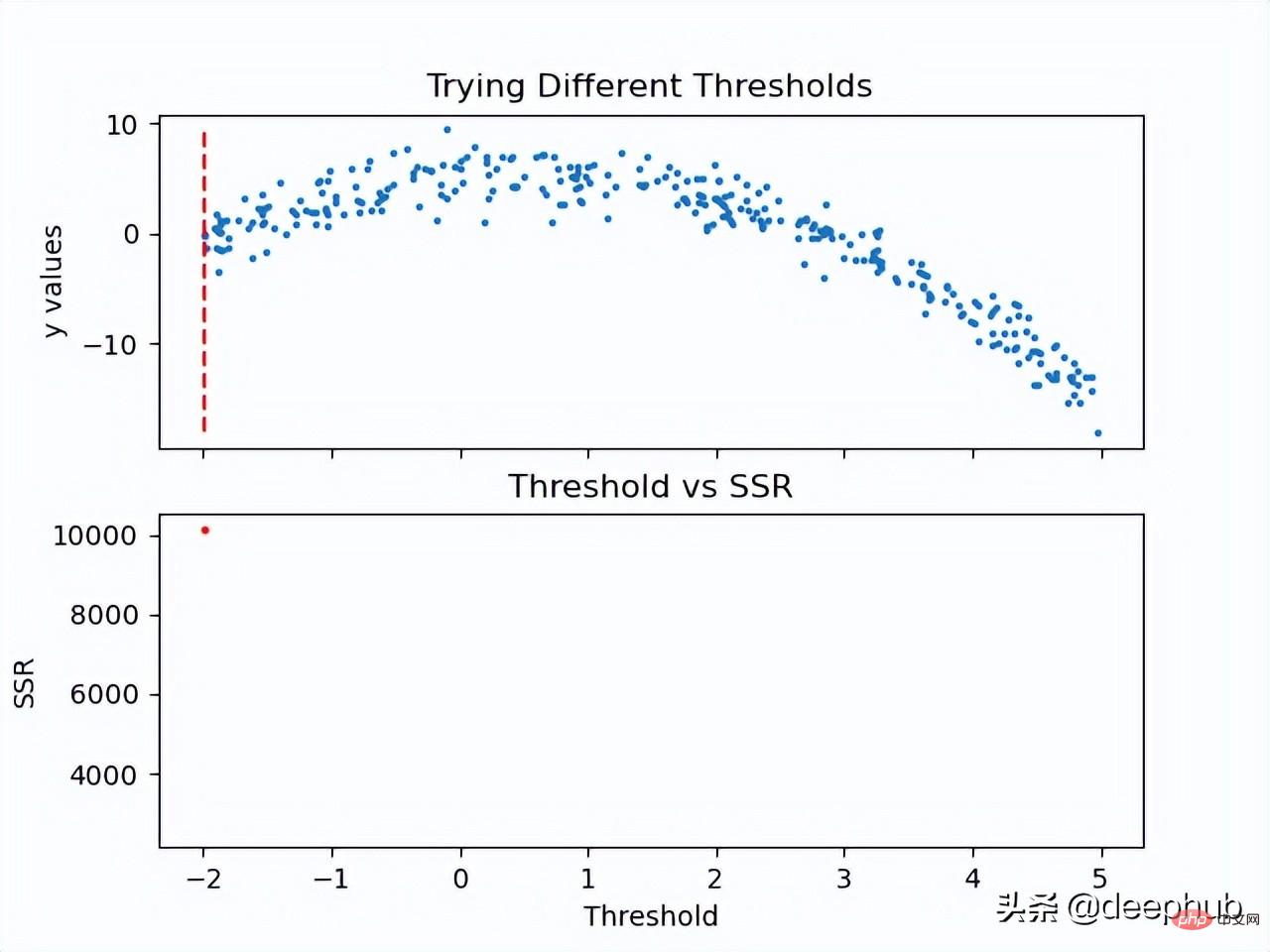
Sekarang nilai SSR bagi ambang dikira, ambang dengan nilai SSR minimum boleh diterima pakai. Gunakan ambang ini untuk membahagikan data latihan kepada dua (bahagian rendah dan tinggi), di mana bahagian rendah akan digunakan untuk mencipta nod anak kiri dan bahagian tinggi akan digunakan untuk mencipta nod anak kanan.

def SSR(r, y): 
return np.sum( (r - y)**2 )

SSRs, thresholds = [], []
for i in range(len(x) - 1):
threshold = x[i:i+2].mean()

low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))

guess_low = low.mean()
guess_high = high.mean()

SSRs.append(SSR(low, guess_low) + SSR(high, guess_high))
thresholds.append(threshold)

print('Minimum residual is: {:.2f}'.format(min(SSRs)))
print('Corresponding threshold value is: {:.4f}'.format(thresholds[SSRs.index(min(SSRs))]))

Salin selepas log masuk

Pepohon regresi tulisan tangan dari awal menggunakan Python

在进入下一步之前，我将使用pandas创建一个df，并创建一个用于寻找最佳阈值的方法。所有这些步骤都可以在没有pandas的情况下完成，这里使用他是因为比较方便。

df = pd.DataFrame(zip(x, y.squeeze()), columns = ['x', 'y'])
def find_threshold(df, plot = False):
SSRs, thresholds = [], []
for i in range(len(df) - 1):
threshold = df.x[i:i+2].mean()
low = df[(df.x <= threshold)]
high = df[(df.x > threshold)]
guess_low = low.y.mean()
guess_high = high.y.mean()
SSRs.append(SSR(low.y.to_numpy(), guess_low) + SSR(high.y.to_numpy(), guess_high))
thresholds.append(threshold)

if plot:
plt.scatter(thresholds, SSRs, s = 3)
plt.show()

return thresholds[SSRs.index(min(SSRs))]

Salin selepas log masuk

创建子节点

在将数据分成两个部分后就可以为低值和高值找到单独的阈值。需要注意的是这里要增加一个停止条件;因为对于每个节点，属于该节点的数据集中的点会变少，所以我们为每个节点定义了最小数据点数量。如果不这样做，每个节点将只使用一个训练值进行预测，会导致过拟合。

可以递归地创建节点，我们定义了一个名为TreeNode的类，它将存储节点应该存储的每一个值。使用这个类我们首先创建根，同时计算它的阈值和预测值。然后递归地创建它的子节点，其中每个子节点类都存储在父类的left或right属性中。

在下面的create_nodes方法中，首先将给定的df分成两部分。然后检查是否有足够的数据单独创建左右节点。如果(对于其中任何一个)有足够的数据点，我们计算阈值并使用它创建一个子节点，用这个新节点作为树再次调用create_nodes方法。

class TreeNode():
def __init__(self, threshold, pred):
self.threshold = threshold
self.pred = pred
self.left = None
self.right = None
def create_nodes(tree, df, stop):
low = df[df.x <= tree.threshold]
high = df[df.x > tree.threshold]

if len(low) > stop:
threshold = find_threshold(low)
tree.left = TreeNode(threshold, low.y.mean())
create_nodes(tree.left, low, stop)

if len(high) > stop:
threshold = find_threshold(high)
tree.right = TreeNode(threshold, high.y.mean())
create_nodes(tree.right, high, stop)

threshold = find_threshold(df)
tree = TreeNode(threshold, df.y.mean())
create_nodes(tree, df, 5)

Salin selepas log masuk

这个方法在第一棵树上进行了修改，因为它不需要返回任何东西。虽然递归函数通常不是这样写的(不返回)，但因为不需要返回值，所以当没有激活if语句时，不做任何操作。

在完成后可以检查此树结构，查看它是否创建了一些可以拟合数据的节点。这里将手动选择第一个节点及其对根阈值的预测。

plt.scatter(x, y, s = 0.5, label = 'Data')
plt.plot([tree.threshold]*2, [-16, 10], 'r--', 
label = 'Root threshold')
plt.plot([tree.right.threshold]*2, [-16, 10], 'g--', 
label = 'Right node threshold')
plt.plot([tree.threshold, tree.right.threshold], 
[tree.right.left.pred]*2,
'g', label = 'Right node prediction')
plt.plot([tree.left.threshold]*2, [-16, 10], 'm--', 
label = 'Left node threshold')
plt.plot([tree.left.threshold, tree.threshold], 
[tree.left.right.pred]*2,
'm', label = 'Left node prediction')
plt.plot([tree.left.left.threshold]*2, [-16, 10], 'k--',
label = 'Second Left node threshold')
plt.legend()

Salin selepas log masuk

Pepohon regresi tulisan tangan dari awal menggunakan Python

这里看到了两个预测:

第一个左节点对高值的预测(高于其阈值)
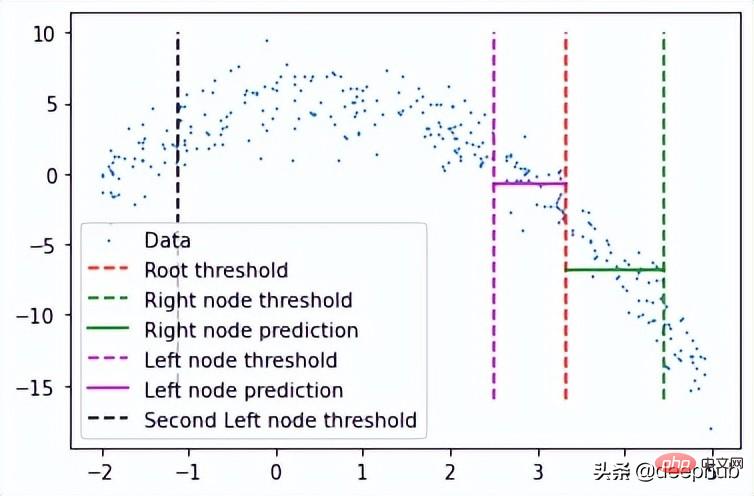
第一个右节点对低值(低于其阈值)的预测

这里我手动剪切了预测线的宽度，因为如果给定的x值达到了这些节点中的任何一个，则将以属于该节点的所有x值的平均值表示，这也意味着没有其他x值参与在该节点的预测中（希望有意义）。

这种树形结构远不止两个节点那么简单，所以我们可以通过如下调用它的子节点来检查一个特定的叶子节点。

tree.left.right.left.left

Salin selepas log masuk

这当然意味着这里有一个向下4个子结点长的分支，但它可以在树的另一个分支上深入得多。

预测

我们可以创建一个预测方法来预测任何给定的值。

def predict(x):
curr_node = tree
result = None
while True:
if x <= curr_node.threshold:
if curr_node.left: curr_node = curr_node.left
else: 
break
elif x > curr_node.threshold:
if curr_node.right: curr_node = curr_node.right
else: 
break

return curr_node.pred

Salin selepas log masuk

预测方法做的是沿着树向下，通过比较我们的输入和每个叶子的阈值。如果输入值大于阈值，则转到右叶，如果小于阈值，则转到左叶，以此类推，直到到达任何底部叶子节点。然后使用该节点自身的预测值进行预测，并与其阈值进行最后的比较。

使用x = 3进行测试(在创建数据时，可以使用上面所写的函数计算实际值。-3**2+3+5 = -1，这是期望值)，我们得到:

predict(3)
# -1.23741

Salin selepas log masuk

计算误差

这里用相对平方误差验证数据

Pepohon regresi tulisan tangan dari awal menggunakan Python

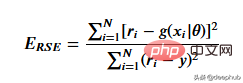
def RSE(y, g): 
return sum(np.square(y - g)) / sum(np.square(y - 1 / len(y)*sum(y)))
x_val = np.random.uniform(-2, 5, 50)
y_val = np.array( [f(i) for i in x_val] ).squeeze()
tr_preds = np.array( [predict(i) for i in df.x] )
val_preds = np.array( [predict(i) for i in x_val] )
print('Training error: {:.4f}'.format(RSE(df.y, tr_preds)))
print('Validation error: {:.4f}'.format(RSE(y_val, val_preds)))

Salin selepas log masuk

可以看到误差并不大，结果如下

Pepohon regresi tulisan tangan dari awal menggunakan Python

概括的步骤

Pepohon regresi tulisan tangan dari awal menggunakan Python

更深入的模型

一个更适合回归树模型的数据：因为我们的数据是多项式生成的数据，所以使用多项式回归模型可以更好地拟合。我们更换一下训练数据，把新函数设为

Pepohon regresi tulisan tangan dari awal menggunakan Python

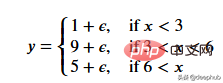
def f(x):
mu, sigma = 0, 0.5
if x < 3: return 1 + np.random.normal(mu, sigma, 1)
elif x >= 3 and x < 6: return 9 + np.random.normal(mu, sigma, 1)
elif x >= 6: return 5 + np.random.normal(mu, sigma, 1)

np.random.seed(1)

x = np.random.uniform(0, 10, num_points)
y = np.array( [f(i) for i in x] )
plt.scatter(x, y, s = 5)

Salin selepas log masuk

Pepohon regresi tulisan tangan dari awal menggunakan Python

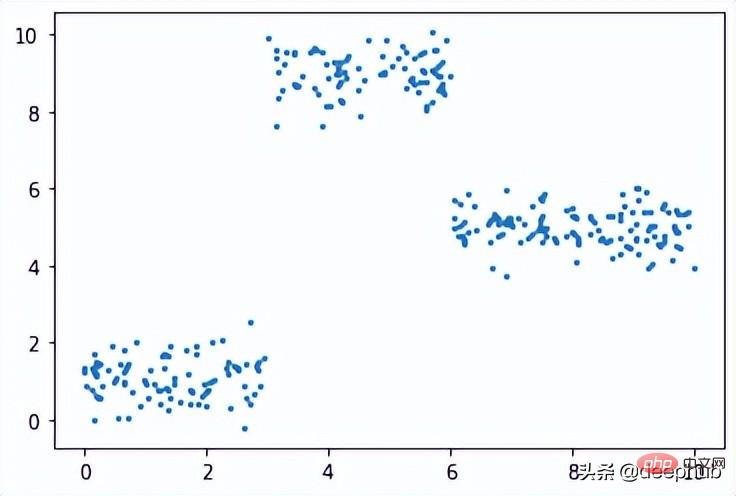
在此数据集上运行了上面的所有相同过程，结果如下

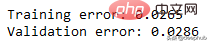
Pepohon regresi tulisan tangan dari awal menggunakan Python

比我们从多项式数据中获得的误差低。

最后共享一下上面动图的代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
#===================================================Create Data
def f(x):
mu, sigma = 0, 1.5
return -x**2 + x + 5 + np.random.normal(mu, sigma, 1)
np.random.seed(1)

x = np.random.uniform(-2, 5, 300)
y = np.array( [f(i) for i in x] )
p = x.argsort()
x = x[p]
y = y[p]
#===================================================Calculate Thresholds
def SSR(r, y): #send numpy array
return np.sum( (r - y)**2 )
SSRs, thresholds = [], []
for i in range(len(x) - 1):
threshold = x[i:i+2].mean()

low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))

guess_low = low.mean()
guess_high = high.mean()

SSRs.append(SSR(low, guess_low) + SSR(high, guess_high))
thresholds.append(threshold)
#===================================================Animated Plot
fig, (ax1, ax2) = plt.subplots(2,1, sharex = True)
x_data, y_data = [], []
x_data2, y_data2 = [], []
ln, = ax1.plot([], [], 'r--')
ln2, = ax2.plot(thresholds, SSRs, 'ro', markersize = 2)
line = [ln, ln2]
def init():
ax1.scatter(x, y, s = 3)
ax1.title.set_text('Trying Different Thresholds')
ax2.title.set_text('Threshold vs SSR')
ax1.set_ylabel('y values')
ax2.set_xlabel('Threshold')
ax2.set_ylabel('SSR')
return line
def update(frame):
x_data = [x[frame:frame+2].mean()] * 2
y_data = [min(y), max(y)]
line[0].set_data(x_data, y_data)
x_data2.append(thresholds[frame])
y_data2.append(SSRs[frame])
line[1].set_data(x_data2, y_data2)
return line
ani = FuncAnimation(fig, update, frames = 298,
init_func = init, blit = True)
plt.show()

Salin selepas log masuk

Atas ialah kandungan terperinci Pepohon regresi tulisan tangan dari awal menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!