gulung! Model penjanaan aliran MIT Poisson mengalahkan model resapan, dengan mengambil kira kualiti dan kelajuan

Pengenalan

Model resapan pada asalnya berasal daripada termodinamik dalam fizik, tetapi baru-baru ini ia telah menjadi popular dalam bidang kecerdasan buatan. Apakah teori fizikal lain yang boleh menggalakkan pembangunan penyelidikan model generatif? Baru-baru ini, penyelidik dari MIT telah diilhamkan oleh teori elektromagnet berdimensi tinggi dan mencadangkan model generatif yang dipanggil Poisson Flow. Secara teorinya, model ini mempunyai imej intuitif dan teori yang ketat secara eksperimen, selalunya lebih baik daripada model resapan dari segi kualiti penjanaan, kelajuan penjanaan dan keteguhan. Artikel ini telah diterima oleh NeurIPS 2022.

• Alamat kertas: https://arxiv.org/abs/2209.11178
• Alamat kod: https://github.com/Newbeeer/Poisson_flow

Diinspirasikan oleh mekanik elektrostatik, para penyelidik mencadangkan model generatif baharu bernama Aliran Poisson model (Poisson Frendah Generatif Model, atau PFGM) . Secara intuitif, penyelidikan ini boleh menganggap titik data N-dimensi sebagai sekumpulan cas positif pada satah z=0, dimensi baharu dalam ruang dimensi N+1 Mereka menjana medan elektrik dalam ruang dimensi tinggi. Bermula dari satah z=0 dan bergerak ke luar di sepanjang garis medan elektrik yang mereka hasilkan, kajian itu dapat menghantar sampel ke hemisfera (seperti ditunjukkan dalam Rajah 1). Arah garisan medan elektrik ini sepadan dengan kecerunan penyelesaian kepada Persamaan Poisson dalam ruang dimensi tinggi. Para penyelidik membuktikan bahawa apabila jejari hemisfera cukup besar, garisan medan elektrik boleh mengubah taburan cas (iaitu taburan data) pada satah z=0 kepada taburan seragam pada hemisfera (Rajah 2).

PFGM mengambil kesempatan daripada keterbalikan talian medan elektrik untuk menjana pengedaran data pada satah z=0: pertama, penyelidik membuat sampel seragam pada hemisfera besar, dan kemudian biarkan sampel mengikut garisan medan elektrik Bergerak dari sfera ke satah z=0 untuk menjana data. Oleh kerana gerakan di sepanjang garis medan elektrik boleh diterangkan oleh persamaan pembezaan biasa (ODE), dalam persampelan sebenar penyelidik hanya perlu menyelesaikan ODE yang ditentukan oleh arah garis medan elektrik. Melalui medan elektrik, PFGM menukar pengedaran mudah pada sfera kepada pengedaran data yang kompleks. Dari perspektif ini, PFGM boleh dianggap sebagai aliran normalizing berterusan (Normalizing Flow).

Dalam percubaan penjanaan imej, PFGM kini merupakan model aliran ternormal yang berprestasi terbaik pada set data standard CIFAR-10, mencapai Ia mencapai skor FID (ukuran kualiti gambar) sebanyak 2.35. Para penyelidik juga menunjukkan kegunaan lain PFGM, ​​seperti keupayaannya untuk mengira kemungkinan imej, melakukan penyuntingan imej, dan skala kepada set data imej resolusi tinggi. Di samping itu, penyelidik mendapati bahawa PFGM mempunyai tiga kelebihan berbanding model penyebaran popular baru-baru ini:

(1) dalam Pada struktur rangkaian yang sama , kualiti sampel yang dijana oleh ODE PFGM adalah jauh lebih baik daripada model resapan (2) Manakala kualiti SDE (persamaan pembezaan stokastik) yang dihasilkan oleh model resapan adalah serupa, ODE PFGM mencapai 10 kali - 20 kali ganda; pecutan;

(3) PFGM lebih teguh daripada model resapan pada struktur rangkaian dengan keupayaan ekspresif yang lebih lemah.

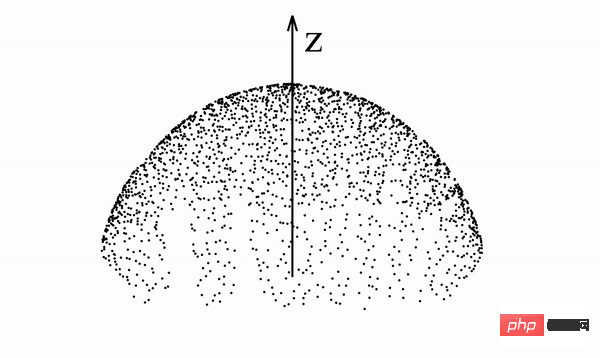
Rajah 1: Titik sampel bergerak di sepanjang garis medan elektrik. Di atas: Pengedaran data adalah dalam bentuk hati; 🎜>

Gambaran Keseluruhan Kaedah

Perhatikan bahawa proses di atas membenamkan data N-dimensi ke dalam ruang N+1-dimensi (z-dimensi tambahan). Untuk memudahkan pembezaan, penyelidik menggunakan x dan 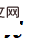untuk mewakili data N-dimensi dan N+1 dimensi. Untuk mendapatkan garis medan elektrik berdimensi tinggi yang disebutkan di atas, persamaan Poisson berikut perlu diselesaikan:

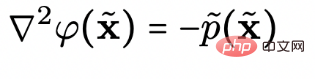
di mana terletak Pengedaran data yang anda ingin hasilkan pada satah z=0 ialah fungsi berpotensi, yang merupakan matlamat penyelesaian penyelidik. Oleh kerana hanya arah garisan medan elektrik yang perlu diketahui, penyelidik memperoleh bentuk analisis kecerunan garisan medan elektrik (kecerunan fungsi potensi):

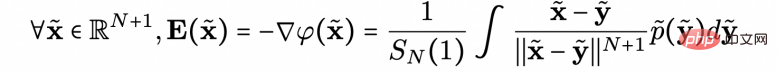
Medan elektrik Trajektori garisan (lihat Rajah 2) boleh diterangkan oleh ODE berikut:

Dalam teorem berikut, penyelidik membuktikan definisi ODE di atas Ia mewakili bijection taburan seragam pada hemisfera berdimensi tinggi dan taburan data pada satah z=0. Kesimpulan ini adalah sama seperti gerak hati dalam Rajah 1 dan 2: pengedaran data boleh dipulihkan melalui talian medan elektrik.

Latihan PFGM​

Diberikan pengagihan data daripada The sampled set data telah digunakan oleh penyelidik untuk menganggarkan kecerunan garis medan elektrik sepadan dengan taburan data:

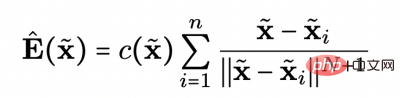
Kecerunan garis medan elektrik ialah sasaran pembelajaran. Kajian ini menggunakan fungsi perturb untuk memilih titik dalam ruang, dan fungsi kehilangan segi empat sama membolehkan rangkaian saraf 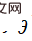mempelajari kecerunan garis medan elektrik yang dinormalkan dalam ruang , algoritma khusus adalah seperti berikut:

Persampelan PFGM​

Selepas mempelajari normalisasi untuk mempelajari kecerunan garis medan elektrik yang dinormalkan dalam ruang , taburan data boleh diambil sampel melalui ODE berikut:

ODE ini secara beransur-ansur menggerakkan sampel dari sfera besar di sepanjang garis medan elektrik ke satah z=0 dengan mengurangkan z. Di samping itu, kajian ini bercadang untuk memproyeksikan taburan seragam pada sfera besar ke atas satah z tertentu untuk memudahkan simulasi ODE dan mempercepatkan lagi pensampelan melalui penggantian berubah-ubah. Sila rujuk Bahagian 3.3 artikel untuk langkah-langkah tertentu.

Hasil eksperimen

Dalam Jadual 1, kajian ini menggunakan set data standard CIFAR-10 untuk menilai model yang berbeza. Pada set data ini, PFGM ialah model aliran ternormal boleh balik berprestasi terbaik , mencapai skor FID 2.35. PFGM berprestasi lebih baik daripada model resapan menggunakan struktur rangkaian yang sama (DDPM++/DDPM++ deep). Para penyelidik juga memerhatikan bahawa walaupun kualiti penjanaan SDE (persamaan pembezaan stokastik) bagi model resapan adalah serupa, PFGM mencapai pecutan 10 kali - 20 kali, mengimbangi kualiti dan kelajuan penjanaan dengan lebih baik. Di samping itu, penyelidik mendapati bahawa PFGM lebih teguh daripada model resapan pada struktur rangkaian dengan keupayaan ekspresif yang lebih lemah, dan masih lebih baik daripada model resapan di bawah keadaan yang sama pada set data berdimensi lebih tinggi. Sila lihat bahagian percubaan artikel untuk mendapatkan butiran. Dalam Rajah 3, kajian menggambarkan proses penjanaan imej PFGM.

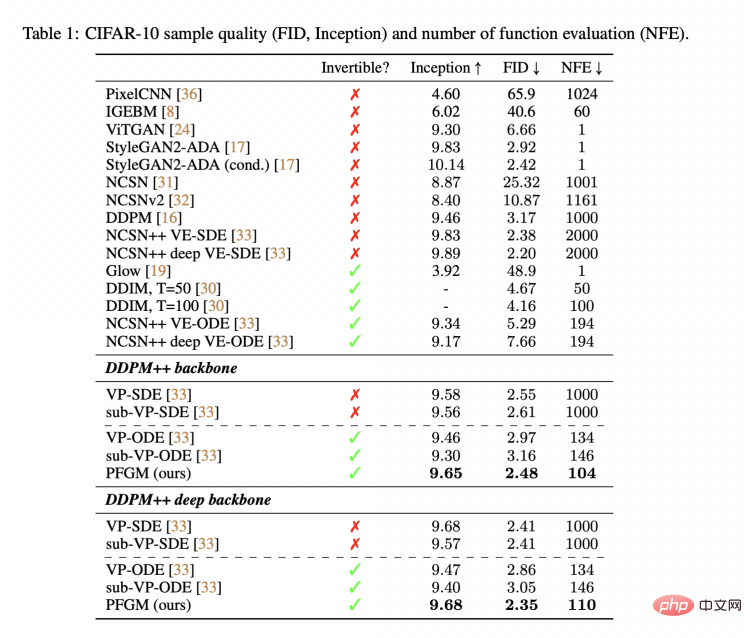
Jadual 1: Kualiti sampel (FID, Inception) dan bilangan langkah pensampelan (NFE) pada data CIFAR-10

Rajah 3: Proses persampelan PFGM pada CIFAR-10, CelebA 64x64, bilik tidur LSUN 256x256

Kesimpulan

Kajian ini mencadangkan Generatif berasaskan Poisson model PFGM bagi Persamaan. Model ini meramalkan kecerunan garis medan elektrik yang dinormalkan dalam ruang lanjutan dimensi N+1 dan disampel oleh ODE yang sepadan bagi garisan medan elektrik. Dalam eksperimen, model yang dikaji dalam kajian ini pada masa ini merupakan model aliran terpiawai terbaik, dan mencapai kesan penjanaan yang lebih baik dan kelajuan pensampelan yang lebih pantas daripada model resapan pada struktur rangkaian yang sama. Proses pensampelan PFGM lebih teguh kepada hingar dan juga boleh diperluaskan kepada set data dimensi yang lebih tinggi. Penyelidik menjangkakan PFGM akan turut berprestasi baik dalam bidang aplikasi lain, seperti penjanaan molekul dan penjanaan data 3D.

Atas ialah kandungan terperinci gulung! Model penjanaan aliran MIT Poisson mengalahkan model resapan, dengan mengambil kira kualiti dan kelajuan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!