写的比较匆忙，测试用例是能全部跑通的，不过考虑内存和效率的话，还有许多需要改进的地方，所以请多指教
题目描述
给定一个二叉树，根节点为第1层，深度为 1。在其第 d 层追加一行值为 v 的节点。
添加规则：给定一个深度值 d （正整数），针对深度为 d-1 层的每一非空节点 N，为 N 创建两个值为 v 的左子树和右子树。
将 N 原先的左子树，连接为新节点 v 的左子树；
将 N 原先的右子树，连接为新节点 v 的右子树。
如果 d 的值为 1，深度 d - 1 不存在，则创建一个新的根节点 v，原先的整棵树将作为 v 的左子树。
Example
【相关课程推荐：JavaScript视频教程】
Input: A binary tree as following: 4 / \ 2 6 / \ / 3 1 5 v = 1d = 2Output: 4 / \ 1 1 / \ 2 6 / \ / 3 1 5
基本思想
二叉树的先序遍历
代码的基本结构
不是最终结构，而是大体的结构
/**
* @param {number} cd:current depth,递归当前深度
* @param {number} td:target depth, 目标深度
*/
var traversal = function (node, v, cd, td) {
// 递归到目标深度，创建新节点并返回
if (cd === td) {
// return 新节点
}
// 向左子树递归
if (node.left) {
node.left = traversal (node.left, v, cd + 1, td);
}
// 向右子树递归
if (node.right) {
node.right = traversal (node.right, v, cd + 1, td);
}
// 返回旧节点
return node;
};
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} v
* @param {number} d
* @return {TreeNode}
*/
var addOneRow = function (root, v, td) {
// 从根节点开始递归
traversal (root, v, 1, td);
return root;
};具体分析
我们可以分类讨论，分三种情况处理
第1种情况：目标深度<=当前递归路径的最大深度
处理方法：val节点替换该目标深度对应的节点，并且
● 如果目标节点原来是左子树，那么重置后目标节点是val节点的左子树
● 如果目标节点原来是右子树，那么重置后目标节点是val节点的右子树
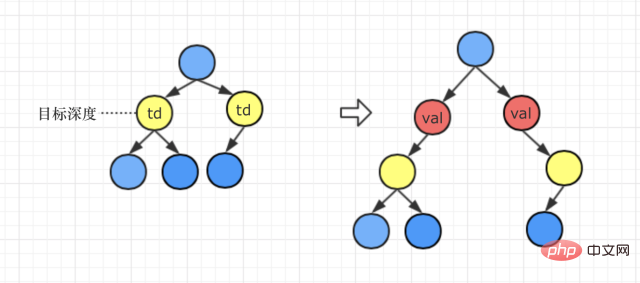
第2种情况：目标深度>当前递归路径的最大深度
阅读题目发现，有这么一个描述：“输入的深度值 d 的范围是：[1，二叉树最大深度 + 1]”
所以呢，当目标深度恰好比当前路径的树的深度再深一层时，处理方式是：
在最底下那一层节点的左右分支新增val节点
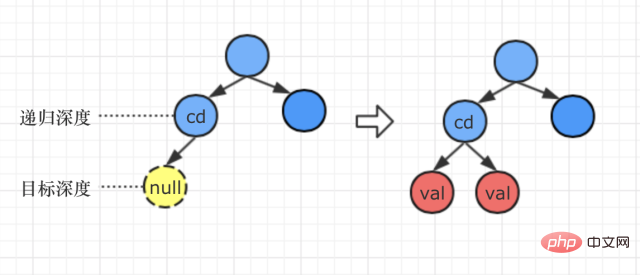
第3种情况：目标深度为1
我们再分析题意，题目里说：“如果 d 的值为 1，深度 d - 1 不存在，则创建一个新的根节点 v，原先的整棵树将作为 v 的左子树。”
这说明当：目标深度为1时，我们的处理方式是这样的
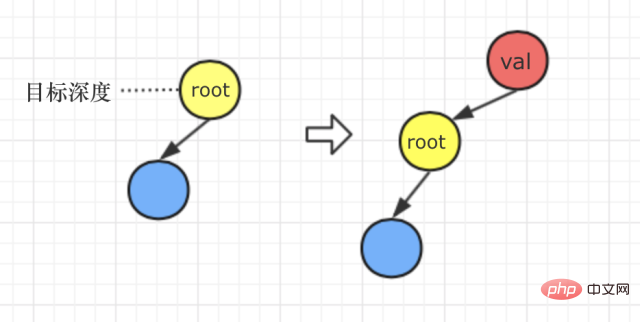
全部代码
/**
* @param {v} val,插入节点携带的值
* @param {cd} current depth,递归当前深度
* @param {td} target depth, 目标深度
* @param {isLeft} 判断原目标深度的节点是在左子树还是右子树
*/
var traversal = function (node, v, cd, td, isLeft) {
debugger;
if (cd === td) {
const newNode = new TreeNode (v);
// 如果原来是左子树，重置后目标节点还是在左子树上，否则相反
if (isLeft) {
newNode.left = node;
} else {
newNode.right = node;
}
return newNode;
}
// 处理上述的第1和第2种情况
if (node.left || (node.left === null && cd + 1 === td)) {
node.left = traversal (node.left, v, cd + 1, td, true);
}
if (node.right || (node.right === null && cd + 1 === td)) {
node.right = traversal (node.right, v, cd + 1, td, false);
}
return node;
};
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} v
* @param {number} d
* @return {TreeNode}
*/
var addOneRow = function (root, v, td) {
// 处理目标深度为1的情况，也就是上述的第3种情况
if (td === 1) {
const n = new TreeNode (v);
n.left = root;
return n;
}
traversal (root, v, 1, td);
return root;
};单词拆分
题目描述
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明：
1.拆分时可以重复使用字典中的单词。
2.你可以假设字典中没有重复的单词。
Example
example1 输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。 注意: 你可以重复使用字典中的单词。 example2 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] 输出: false来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/word-break
基本思想
动态规划
具体分析
动态规划的关键点是：寻找状态转移方程
有了这个状态转移方程，我们就可以根据上一阶段状态和决策结果，去求出本阶段的状态和结果
然后，就可以从初始值，不断递推求出最终结果。
在这个问题里，我们使用一个一维数组来存放动态规划过程的递推数据
假设这个数组为dp，数组元素都为true或者false,
dp[N] 存放的是字符串s中从0到N截取的子串是否是“可拆分”的布尔值
让我们从一个具体的中间场景出发来思考计算过程
假设我们有
wordDict = ['ab','cd','ef'] s ='abcdef'
并且假设目前我们已经得出了N=1到N=5的情况，而现在需要计算N=6的情况
或者说，我们已经求出了dp[1] 到dp[5]的布尔值，现在需要计算dp[6] = ?
该怎么计算呢？
现在新的字符f被加入到序列“abcde”的后面，如此以来，就新增了以下几种6种需要计算的情况
A序列 + B序列1.abcdef + "" 2.abcde + f3.abcd + ef4.abc + def5.ab + cdef6.a + bcdef 注意：当A可拆且B可拆时，则A+B也是可拆分的
从中我们不难发现两点
1. 当A可拆且B可拆时，则A+B也是可拆分的
2. 这6种情况只要有一种组合序列是可拆分的，abcdef就一定是可拆的，也就得出dp[6] = true了
下面是根据根据已有的dp[1] 到dp[5]的布尔值，动态计算dp[6] 的过程
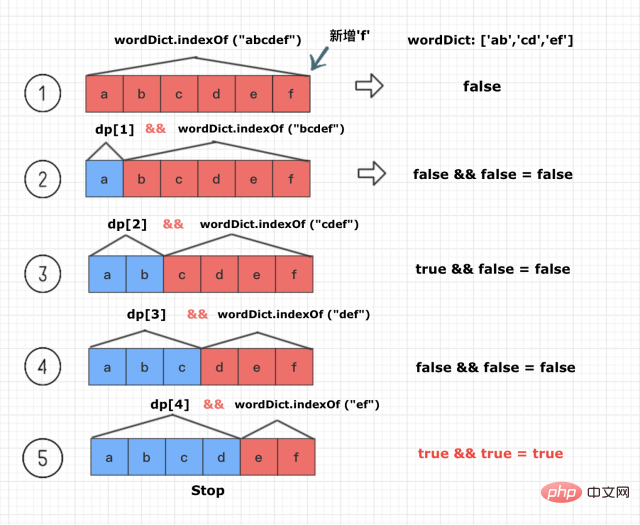
（注意只要计算到可拆，就可以break循环了）
具体代码
var initDp = function (len) {
let dp = new Array (len + 1).fill (false);
return dp;
};
/**
* @param {string} s
* @param {string[]} wordDict
* @return {boolean}
*/
var wordBreak = function (s, wordDict) {
// 处理空字符串
if (s === '' && wordDict.indexOf ('') === -1) {
return false;
}
const len = s.length;
// 默认初始值全部为false
const dp = initDp (len);
const a = s.charAt (0);
// 初始化动态规划的初始值
dp[0] = wordDict.indexOf (a) === -1 ? false : true;
dp[1] = wordDict.indexOf (a) === -1 ? false : true;
// i:end
// j:start
for (let i = 1; i < len; i++) {
for (let j = 0; j <= i; j++) {
// 序列[0,i] = 序列[0,j] + 序列[j,i]
// preCanBreak表示序列[0,j]是否是可拆分的
const preCanBreak = dp[j];
// 截取序列[j,i]
const str = s.slice (j, i + 1);
// curCanBreak表示序列[j,i]是否是可拆分的
const curCanBreak = wordDict.indexOf (str) !== -1;
// 情况1: 序列[0,j]和序列[j,i]都可拆分，那么序列[0,i]肯定也是可拆分的
const flag1 = preCanBreak && curCanBreak;
// 情况2: 序列[0,i]本身就存在于字典中，所以是可拆分的
const flag2 = curCanBreak && j === 0;
if (flag1 || flag2) {
// 设置bool值，本轮计算结束
dp[i + 1] = true;
break;
}
}
}
// 返回最后结果
return dp[len];
};全排列
题目描述
给定一个没有重复数字的序列，返回其所有可能的全排列。
Example
输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
基本思想
回溯法
具体分析
1. 深度优先搜索搞一波，index在递归中向前推进
2. 当index等于数组长度的时候，结束递归，收集到results中（数组记得要深拷贝哦）
3. 两次数字交换的运用，计算出两种情况
总结
想不通没关系，套路一波就完事了
具体代码
var swap = function (nums, i, j) {
const temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
};
var recursion = function (nums, results, index) {
// 剪枝
if (index >= nums.length) {
results.push (nums.concat ());
return;
}
// 初始化i为index
for (let i = index; i < nums.length; i++) {
// index 和 i交换？？
// 统计交换和没交换的两种情况
swap (nums, index, i);
recursion (nums, results, index + 1);
swap (nums, index, i);
}
};
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function (nums) {
const results = [];
recursion (nums, results, 0);
return results;
};本文来自 js教程 栏目，欢迎学习！
Atas ialah kandungan terperinci JavaScript中二叉树，动态规划和回溯法（案例分析）. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
