
3203. Cari Diameter Minimum Selepas Mencantum Dua Pokok
Kesukaran: Sukar
Topik: Pokok, Depth-First Search, Breadth-First Search, Graph
Terdapat dua pokok tidak berarah dengan nod n dan m, masing-masing bernombor dari 0 hingga n - 1 dan dari 0 hingga m - 1. Anda diberi dua tatasusunan integer 2D masing-masing tepi1 dan tepi2 panjang n - 1 dan m - 1, di mana edges1[i] = [ai, bi] menunjukkan bahawa terdapat ialah tepi antara nod ai dan bi dalam pokok pertama dan tepi2[i] = [ui, vi] menunjukkan bahawa terdapat tepi antara nod ui dan v i dalam pokok kedua.
Anda mesti menyambungkan satu nod daripada pokok pertama dengan satu lagi nod daripada pokok kedua dengan tepi.
Kembali minimum yang mungkin diameter pokok yang terhasil.
diameter pokok ialah panjang laluan terpanjang antara mana-mana dua nod dalam pokok itu.
Contoh 1:
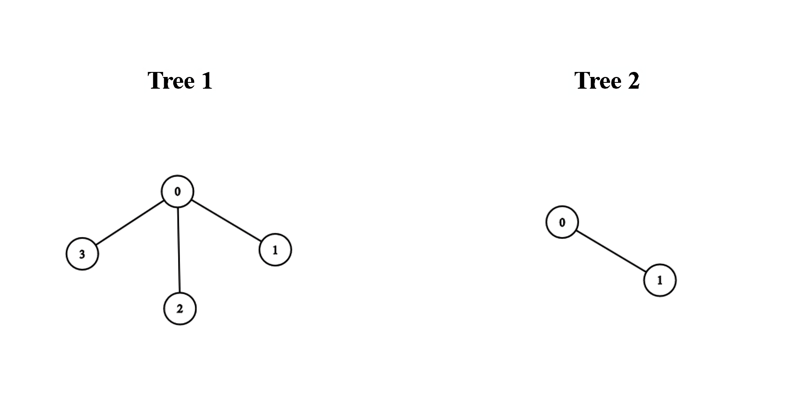
Contoh 2:
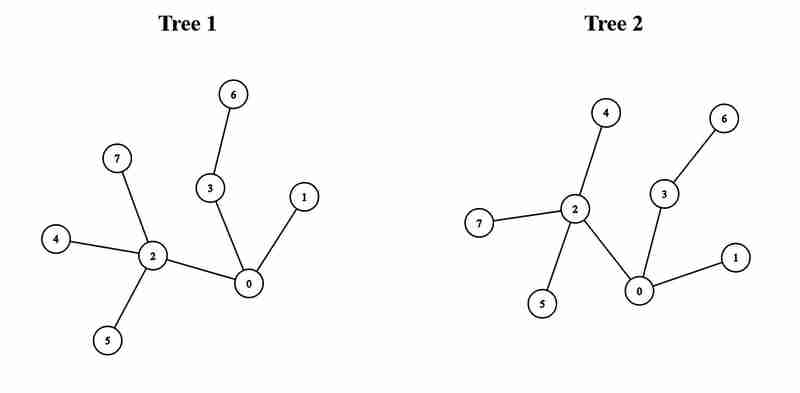
Kekangan:
Petunjuk:
Penyelesaian:
Kita perlu mendekatinya selangkah demi selangkah dengan fokus pada pemahaman cara mengira diameter pokok dan cara penyambungan dua pokok mempengaruhi diameter keseluruhan.
Cari diameter setiap pokok:
Tentukan nod optimum untuk disambungkan:
Meminimumkan jumlah diameter:
Mari laksanakan penyelesaian ini dalam PHP: 3203. Cari Diameter Minimum Selepas Mencantum Dua Pokok
Penjelasan:
Fungsi Pembantu BFS: Fungsi bfs mengira nod paling jauh daripada nod permulaan yang diberikan dan mengembalikan tatasusunan jarak dan nod paling jauh ditemui. Ini penting untuk mengira diameter pokok.
Dapatkan Diameter dan Pusat: Fungsi getDiameterAndCenter mencari diameter pokok dan pusatnya. Bahagian tengah pokok adalah penting untuk meminimumkan diameter pokok baharu apabila menggabungkan dua pokok.
Penyelesaian Utama:
- Kami mula-mula membina senarai bersebelahan untuk kedua-dua pokok.
- Kami mengira diameter dan pusat untuk kedua-dua pokok.
- Kami melakukan BFS dari pusat kedua-dua pokok untuk mendapatkan laluan terpanjang dalam setiap pokok.
- Akhir sekali, kami mengira maksimum tiga nilai untuk mendapatkan diameter minimum pokok yang digabungkan.
Kerumitan Masa:
Pendekatan ini memastikan kami mencari diameter minimum yang mungkin apabila menggabungkan kedua-dua pokok.
Pautan Kenalan
Jika anda mendapati siri ini membantu, sila pertimbangkan untuk memberi repositori bintang di GitHub atau berkongsi siaran pada rangkaian sosial kegemaran anda ?. Sokongan anda amat bermakna bagi saya!
Jika anda mahukan kandungan yang lebih berguna seperti ini, sila ikuti saya:
Atas ialah kandungan terperinci Cari Diameter Minimum Selepas Mencantum Dua Pokok. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk memadam alamat WeChat saya
Bagaimana untuk memadam alamat WeChat saya
 Bagaimana untuk mencari jumlah item genap dalam tatasusunan dalam php
Bagaimana untuk mencari jumlah item genap dalam tatasusunan dalam php
 ralat mysql 10060
ralat mysql 10060
 Cara menutup tetingkap yang dibuka dengan tetingkap.buka
Cara menutup tetingkap yang dibuka dengan tetingkap.buka
 Penggunaan anotasi halaju
Penggunaan anotasi halaju
 Bagaimana untuk menyemak sama ada port 445 ditutup
Bagaimana untuk menyemak sama ada port 445 ditutup
 Periksa tingkap penghunian port
Periksa tingkap penghunian port
 Bagaimana untuk menyelaraskan kotak teks dalam html
Bagaimana untuk menyelaraskan kotak teks dalam html




