
2290. Penyingkiran Halangan Minimum untuk Mencapai Sudut
Kesukaran: Sukar
Topik: Tatasusunan, Keluasan Carian Pertama, Graf, Timbunan (Baris Gilir Keutamaan), Matriks, Laluan Terpendek
Anda diberikan grid tatasusunan integer 2D 0-diindeks bersaiz m x n. Setiap sel mempunyai satu daripada dua nilai:
Anda boleh bergerak ke atas, bawah, kiri atau kanan dari dan ke sel kosong.
Kembalikan bilangan minimum halangan untuk alih keluar supaya anda boleh bergerak dari sudut kiri atas (0, 0) ke kanan bawah sudut (m - 1, n - 1).
Contoh 1:

Contoh 2:
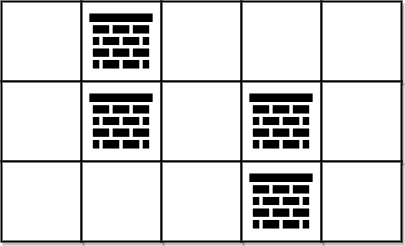
Kekangan:
Petunjuk:
Penyelesaian:
Kita perlu memodelkan masalah ini menggunakan graf di mana setiap sel dalam grid ialah nod. Matlamatnya adalah untuk menavigasi dari sudut kiri atas (0, 0) ke sudut kanan bawah (m-1, n-1), sambil meminimumkan bilangan halangan (1s) yang perlu kami alih keluar.
Perwakilan Graf:
Pilihan Algoritma:
0-1 BFS:
Mari laksanakan penyelesaian ini dalam PHP: 2290. Penyingkiran Halangan Minimum untuk Mencapai Sudut
Penjelasan:
Penghuraian Input:
- Grid diambil sebagai tatasusunan 2D.
- Baris dan lajur dikira untuk semakan sempadan.
Pelaksanaan Deque:
- SplDoublyLinkedList digunakan untuk mensimulasikan deque. Ia menyokong penambahan elemen di hadapan (nyah anjakan) atau belakang (tolak).
Susun Yang Dilawati:
- Menjejaki sel yang telah dilawati untuk mengelakkan pemprosesan berlebihan.
0-1 BFS Logik:
- Mulakan dari (0, 0) dengan kos 0.
- Untuk setiap sel jiran:
- Jika kosong (grid[nx][ny] == 0), tambahkannya pada bahagian hadapan deque dengan kos yang sama.
- Jika ia adalah halangan (grid[nx][ny] == 1), tambahkannya ke bahagian belakang deque dengan kos tambahan.
Kembalikan Keputusan:
- Apabila sudut kanan bawah dicapai, pulangkan kos.
- Jika tiada laluan yang sah wujud (walaupun masalah menjamin satu), kembalikan -1.
Kerumitan:
Pelaksanaan ini berfungsi dengan cekap dalam kekangan yang diberikan.
Pautan Kenalan
Jika anda mendapati siri ini membantu, sila pertimbangkan untuk memberi repositori bintang di GitHub atau berkongsi siaran pada rangkaian sosial kegemaran anda ?. Sokongan anda amat bermakna bagi saya!
Jika anda mahukan kandungan yang lebih berguna seperti ini, sila ikuti saya:
Atas ialah kandungan terperinci Penyingkiran Halangan Minimum untuk Mencapai Sudut. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Beberapa cara untuk menangkap data
Beberapa cara untuk menangkap data
 Bagaimana untuk menetapkan ketelusan dalam CSS
Bagaimana untuk menetapkan ketelusan dalam CSS
 Mengapa kad telefon mudah alih terhad kepada panggilan kecemasan?
Mengapa kad telefon mudah alih terhad kepada panggilan kecemasan?
 Penggunaan fungsi keluar dalam bahasa c
Penggunaan fungsi keluar dalam bahasa c
 Bagaimana untuk menyemak IP komputer
Bagaimana untuk menyemak IP komputer
 Sistem oa mana yang lebih baik?
Sistem oa mana yang lebih baik?
 Bagaimana untuk menukar phpmyadmin kepada bahasa Cina
Bagaimana untuk menukar phpmyadmin kepada bahasa Cina
 Apakah kemahiran yang diperlukan untuk bekerja dalam industri PHP?
Apakah kemahiran yang diperlukan untuk bekerja dalam industri PHP?




