
Pokok carian binari ialah struktur data yang membolehkan kami menyimpan senarai nombor yang diisih dalam masa yang singkat. Ia juga dipanggil pokok binari kerana setiap nod pokok hanya boleh mempunyai dua adik beradik. Pohon carian binari boleh digunakan untuk mencari kehadiran nombor; ia dipanggil pokok carian. Kerumitan masa berjalan ialah masa O(log(n)); ciri-ciri yang membezakan pokok carian binari daripada pokok binari asas adalah seperti berikut –
Mulakan Kursus Pembangunan Perisian Percuma Anda
Pembangunan web, bahasa pengaturcaraan, ujian perisian & lain-lain
1. Nod subpokok kiri semuanya lebih kecil daripada nod akar.
2. Nod subpokok kanan semuanya lebih besar daripada nod akar.
3. Setiap nod subpokok adalah juga BST, bermakna ia mempunyai dua kualiti yang sama seperti nod itu sendiri.
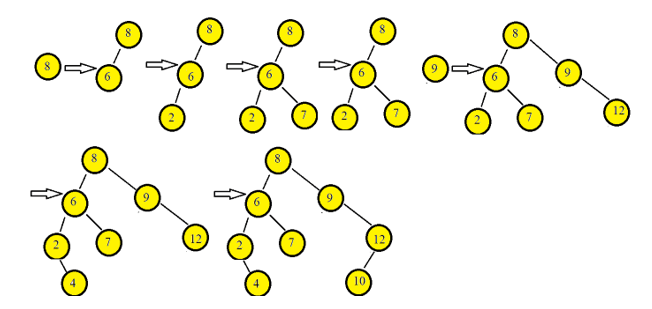
1. Biarkan tatasusunan yang ditentukan ialah:
Tatasusunan yang diberikan: [8, 6, 2, 7, 9, 12, 4, 10]
2. Mari kita mulakan dengan elemen atas 43. Masukkan 43 sebagai akar pokok.
3. Jika elemen seterusnya kurang daripada elemen nod akar, ia hendaklah dimasukkan sebagai punca subpokok kiri.
4. Jika tidak, ia harus dimasukkan sebagai akar sub-pokok kanan.
Imej di bawah menggambarkan proses membina pepohon carian binari menggunakan elemen yang disediakan.
Operasi pokok carian binari:
Operasi yang disokong oleh pepohon carian binari di Jawa ditunjukkan dalam senarai di bawah –
1. Mencari dalam BST – Dalam pepohon carian binari, mencari kedudukan elemen tertentu.
2. Sisipan dalam BST – Menambah elemen baharu pada pepohon carian binari di lokasi yang betul memastikan bahawa sifat pepohon carian binari tidak rosak.
3. Pemadaman dalam BST – Alih keluar nod tertentu dalam pepohon carian binari. Walau bagaimanapun, bergantung pada bilangan anak yang dimiliki oleh nod, terdapat pelbagai senario pemadaman.
Contoh pepohon carian binari di Jawa untuk melaksanakan operasi pada pepohon carian binari –
// Program ini boleh diuji dalam Eclipse IDE, JAVA 11
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}Output:
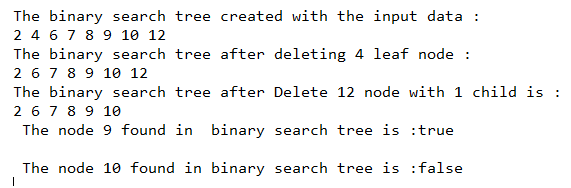
Seperti dalam program di atas, kelas binarySearchTree dicipta, yang mengandungi Nod kelas dalam yang lain dan juga mengandungi pembina dan kaedah. Kaedah yang ditakrifkan dalam kelas ialah deleteKey(), delete(), minKey(), insertKey(), insert(), inorder(), searchKey(), dan search() untuk melaksanakan operasi tertentu. Dalam fungsi utama, objek kelas binarySearchTree dicipta, masukkan beberapa elemen ke dalamnya dan seterusnya panggil kaedah kelas Pokok Carian binari pada objeknya, seperti yang dilihat dalam output di atas.
Pokok carian binari juga dikenali sebagai pokok binari kerana setiap nod pokok hanya boleh mempunyai dua adik beradik. Pepohon carian binari ialah struktur data yang membolehkan menyimpan senarai nombor yang diisih dalam masa yang singkat. Operasi yang boleh dilakukan pada pepohon carian binari: melintasi, memasukkan, memadam dan mencari.
Atas ialah kandungan terperinci Pokok Carian Binari di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




