 Peranti teknologi
Peranti teknologi
 AI
AI
 Mengapa saya tidak tahu semasa saya belajar penjanaan garis: Terdapat hubungan kesetaraan antara matriks dan graf?
Mengapa saya tidak tahu semasa saya belajar penjanaan garis: Terdapat hubungan kesetaraan antara matriks dan graf?
Mengapa saya tidak tahu semasa saya belajar penjanaan garis: Terdapat hubungan kesetaraan antara matriks dan graf?
Matriks sukar difahami, tetapi ia mungkin berbeza dari perspektif lain.
Apabila belajar matematik, kita sering kecewa dengan kesukaran dan keabstrakan pengetahuan yang kita pelajari; tetapi kadang-kadang, hanya dengan mengubah perspektif, kita boleh mencari penyelesaian yang mudah dan intuitif untuk masalah itu. Sebagai contoh, semasa kita mempelajari formula jumlah kuasa dua (a+b)² semasa kita masih kanak-kanak, kita mungkin tidak faham mengapa ia sama dengan a²+2ab+b² Kita hanya tahu bahawa ia ditulis seperti ini dalam buku dan guru meminta kami mengingatnya seperti ini; sehingga satu hari kami melihat saya melihat gambar animasi ini:
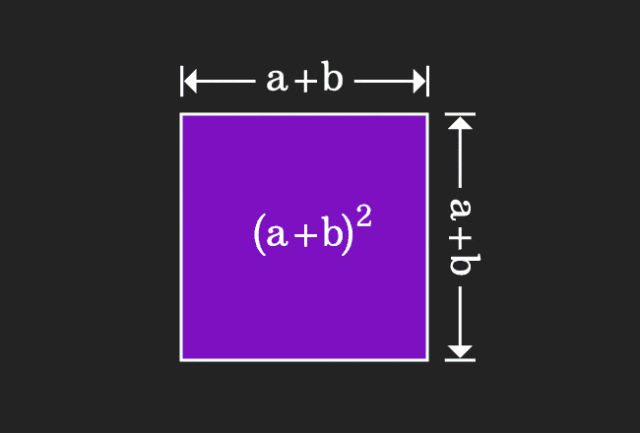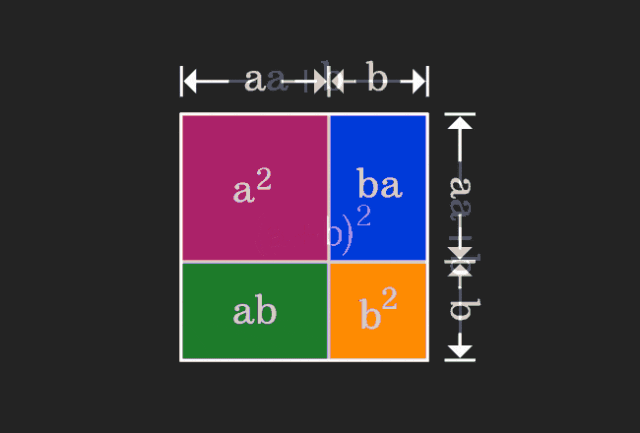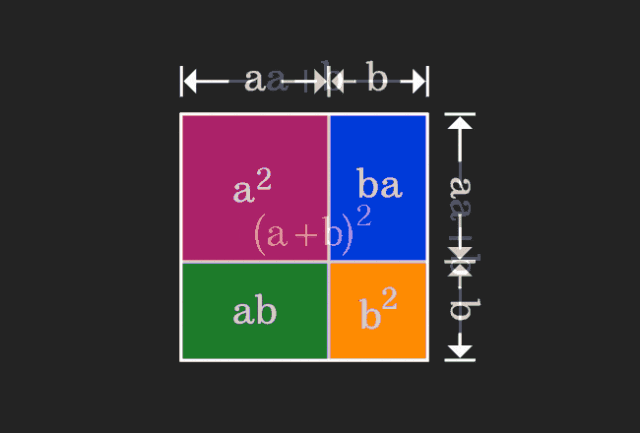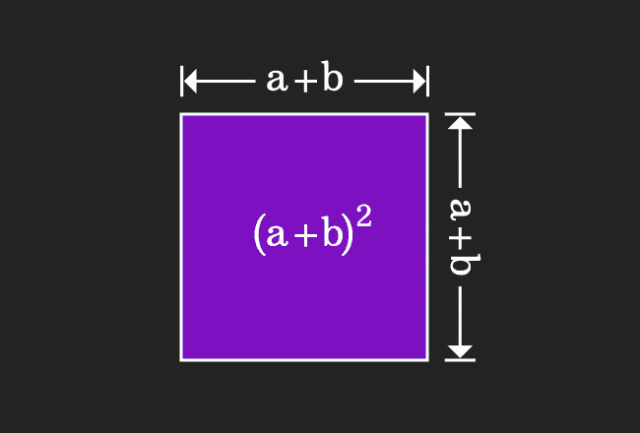
Saya tiba-tiba menyedari bahawa kita boleh memahaminya dari perspektif geometri!
Kini, rasa pencerahan ini muncul semula: matriks bukan negatif boleh ditukar secara sama kepada graf terarah yang sepadan!
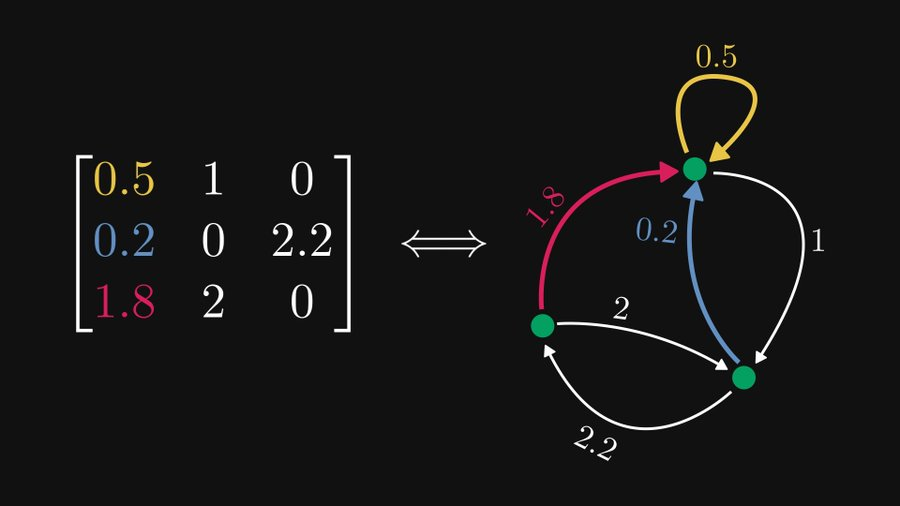
Seperti yang ditunjukkan dalam rajah di bawah, matriks 3×3 di sebelah kiri sebenarnya boleh diwakili secara setara sebagai graf terarah yang mengandungi tiga nod di sebelah kanan, dan perwakilan ini sangat membantu untuk kedua-dua teori matriks dan graf.
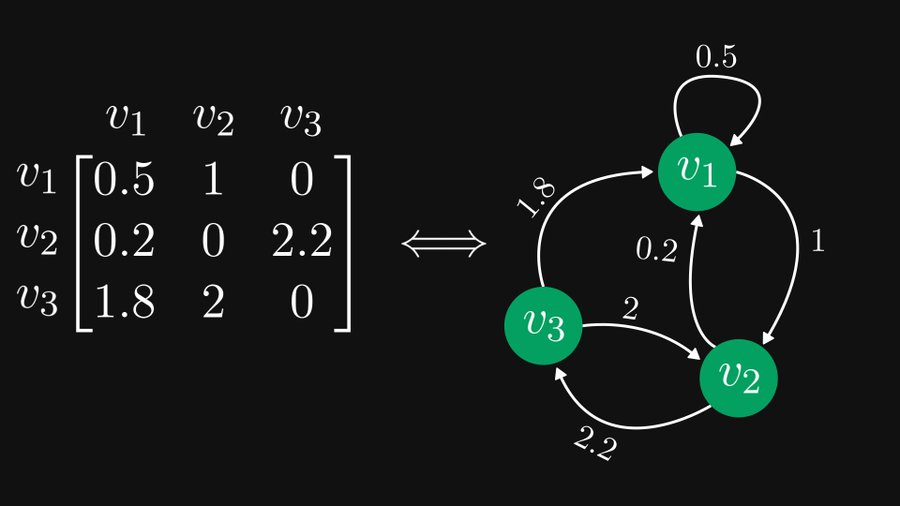
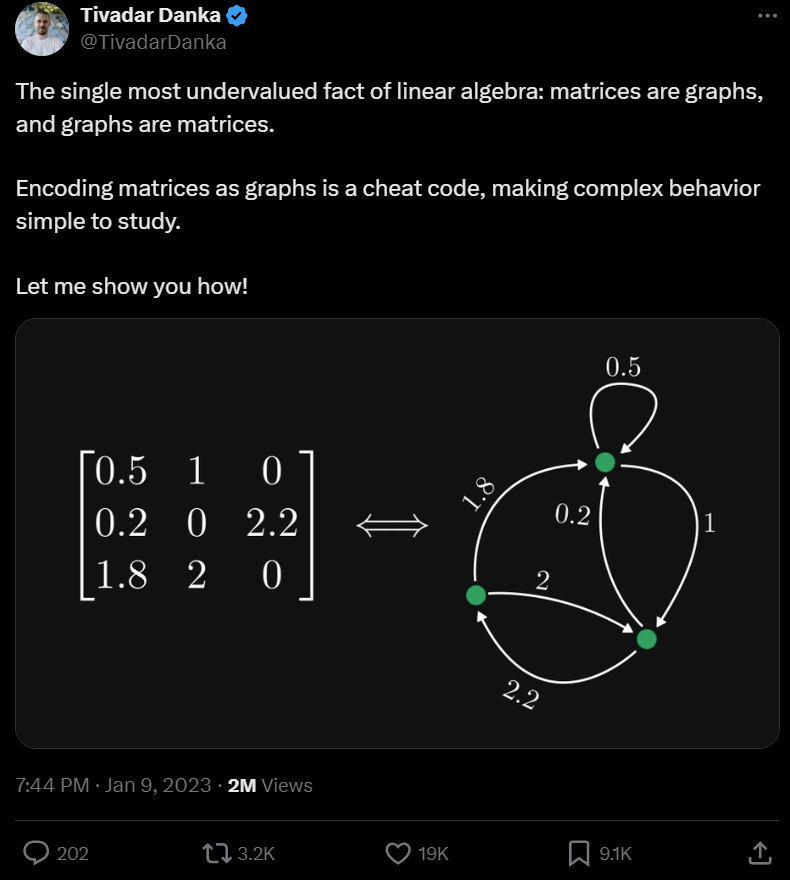
Contoh ini datang daripada Tivadar Danka, seorang ahli matematik yang komited untuk menjadikan matematik boleh diakses oleh semua orang. Ahli matematik yang mengisytiharkan dirinya sebagai "kebaikan huru-hara" dengan jelas memperkenalkan kesetaraan matriks dan graf ini serta kegunaannya dalam satu siri tweet dan catatan blog. Sehingga kini, tweet tersebut telah dibaca lebih daripada 2 juta kali, menerima lebih daripada 3,200 tweet semula dan 9,100 kegemaran.
Valens matriks dan graf berarah
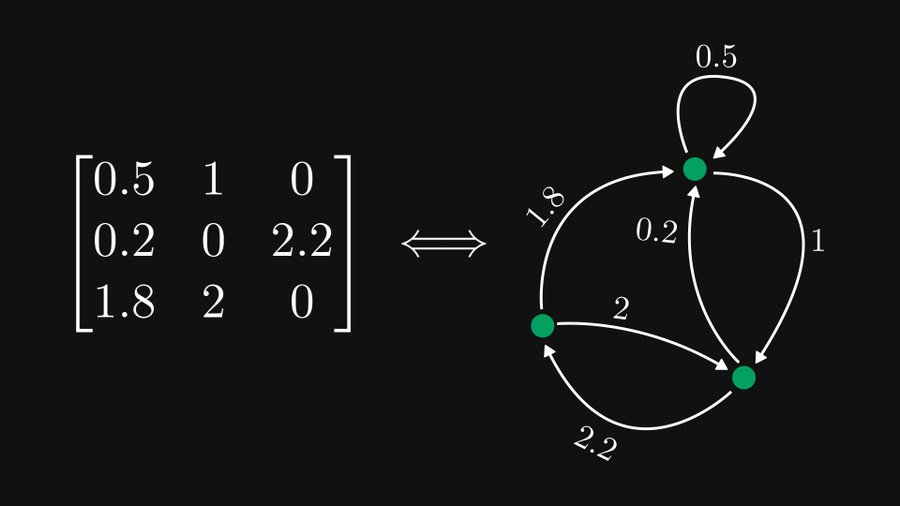
Seperti yang ditunjukkan dalam contoh di atas, jika kita menganggap setiap baris sebagai nod, setiap elemen boleh diwakili sebagai tepi terarah dan berwajaran. Sudah tentu, 0 elemen boleh diabaikan. Jika elemen terletak di baris i dan lajur j, ia sepadan dengan tepi dari nod i ke nod j.
Ini mungkin kelihatan rumit pada pandangan pertama, tetapi kita boleh melihat salah satu nod terlebih dahulu.
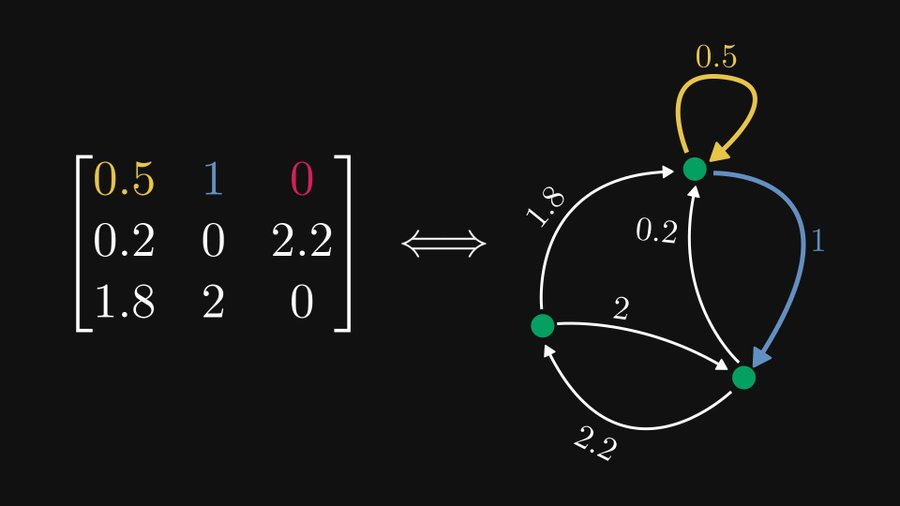
Seperti yang ditunjukkan dalam rajah, untuk matriks 3×3 ini, baris 1 sepadan dengan nod paling atas (kami memanggilnya nod 1 di sini), yang mengandungi 3 elemen tetapi satu daripadanya ialah 0, jadi Nod ini memanjangkan dua tepi. Tepi kuning mewakili unsur 0.5 pada (1,1), jadi ia adalah tepi terarah yang menghala ke dirinya sendiri dengan berat 0.5. Begitu juga, tepi biru ialah tepi yang menghala ke nod 2 dan mempunyai berat 1.
Dengan cara ini, kita boleh menganalisis bahawa lajur ke-i matriks sepadan dengan semua tepi yang menghala ke nod ke-i.
Apakah kegunaan ungkapan setara ini?
Persamaan antara matriks bukan negatif dan graf terarah ini bukan sahaja dapat membantu kita memahami dengan lebih baik matriks dan operasinya, tetapi juga membantu memudahkan beberapa proses pengiraan, ini juga boleh membantu kita bermula dari rajah Pemahaman perspektif baharu.
Sebagai contoh, kuasa matriks sepadan dengan berjalan dalam graf.
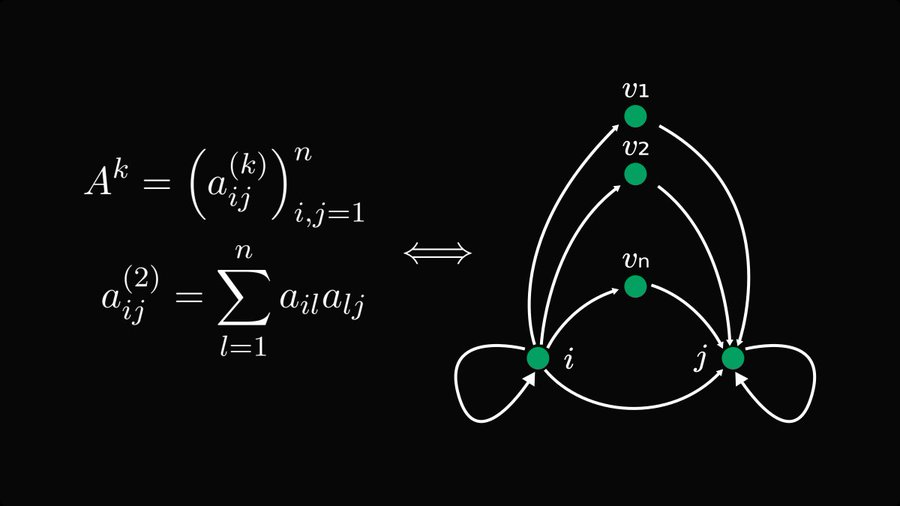
Seperti yang ditunjukkan dalam rajah di atas, untuk kuasa ke-k bagi matriks persegi n×n A, proses penjumlahan setiap elemen akan menggabungkan semua kemungkinan berjalan langkah-k.
Sebagai contoh, andaikan kita ingin mengira kuasa dua matriks 3×3 di atas. . = 0.45. Akhirnya, kita boleh mendapatkan hasil yang lengkap sebagai:

Tetapi jika kita menggunakan kaedah graf berjalan di atas, kita boleh mendapatkan hasilnya dengan berjalan di laluan. Begitu juga, untuk elemen pertama matriks hasil, kita perlu merumuskan semua laluan berjalan 2 langkah yang memenuhi a_{1,l}→a_{l,1}.
Walau bagaimanapun, jika graf terarah ini mewakili keadaan rantai Markov, kuasa dua matriks kebarangkalian peralihannya pada asasnya mewakili kebarangkalian rantai mencapai keadaan tertentu selepas 2 langkah.
Bukan itu sahaja, menggunakan graf untuk mewakili matriks juga boleh memberi kita pemahaman yang mendalam tentang struktur matriks bukan negatif. Untuk melakukan ini, Danka berkata kita perlu terlebih dahulu memahami konsep "komponen bersambung kuat."
Komponen bersambung kuat
Apakah komponen bersambung kuat? Untuk graf terarah, jika setiap nod lain dalam graf boleh dicapai dari setiap nod, kita katakan bahawa graf itu bersambung kuat. Seperti yang ditunjukkan di bawah.
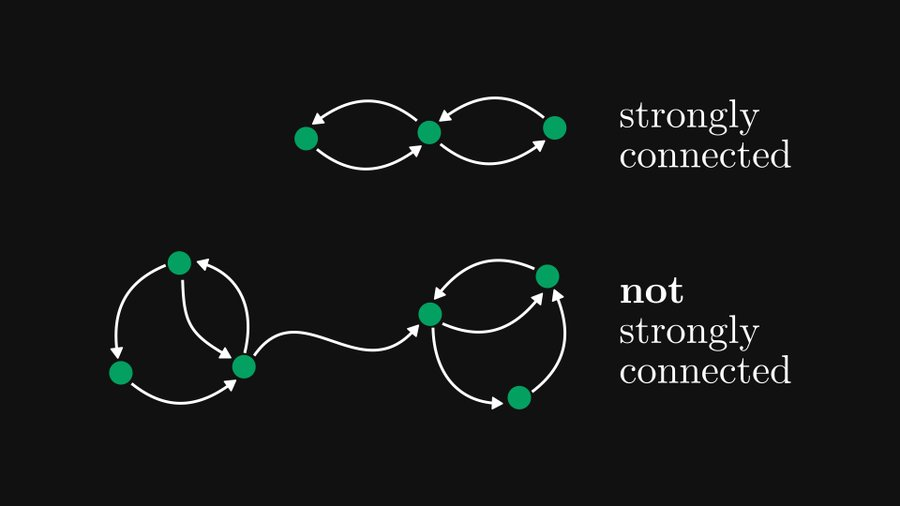
Komponen bersambung kuat merujuk kepada bahagian/subgraf dalam graf terarah yang boleh mencapai ketersambungan yang kuat. Seperti yang ditunjukkan dalam rajah di bawah, terdapat komponen bersambung kuat di kiri dan kanan, manakala tepi putih di tengah tidak tergolong dalam mana-mana komponen bersambung kuat.
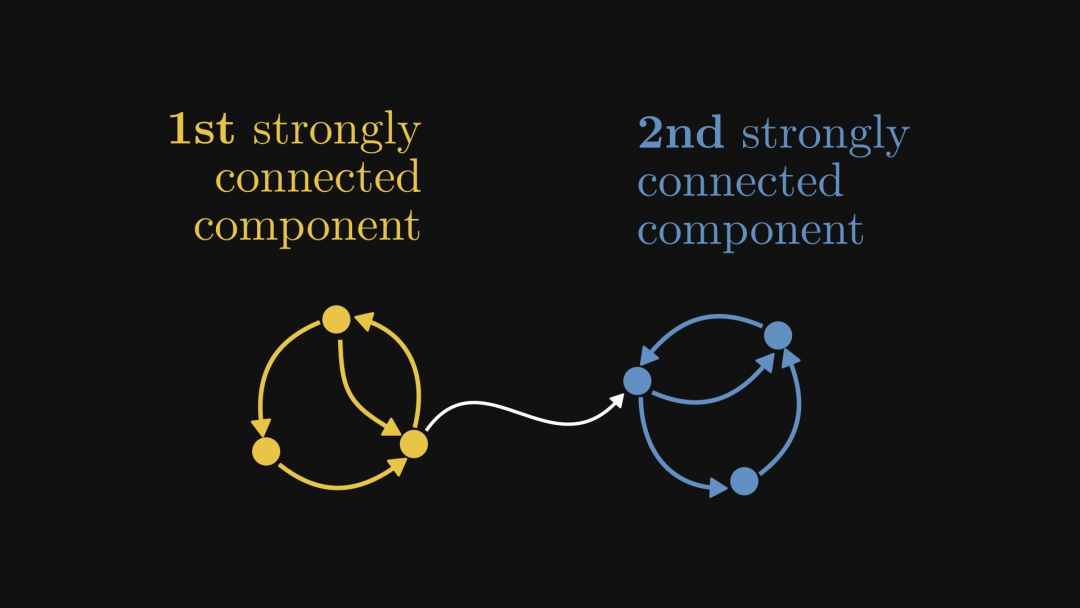
Rajah di bawah menunjukkan satu lagi contoh, di mana bahagian kuning ialah komponen bersambung kuat:
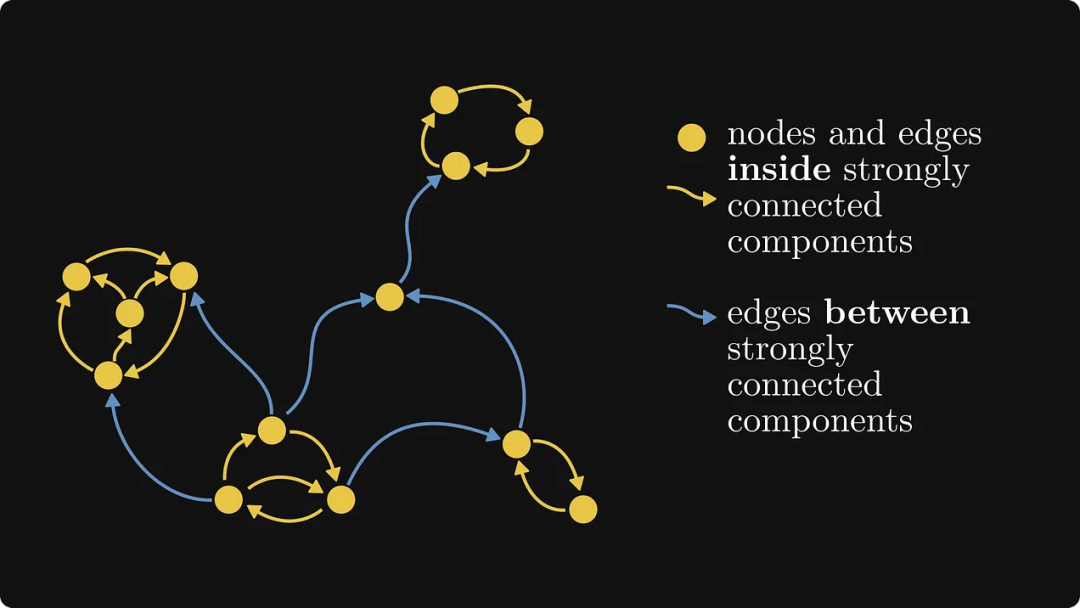
Matriks yang sepadan dengan graf bersambung kuat ialah matriks tidak boleh dikurangkan, manakala semua matriks lain dalam matriks bukan negatif adalah matriks boleh dikurangkan.
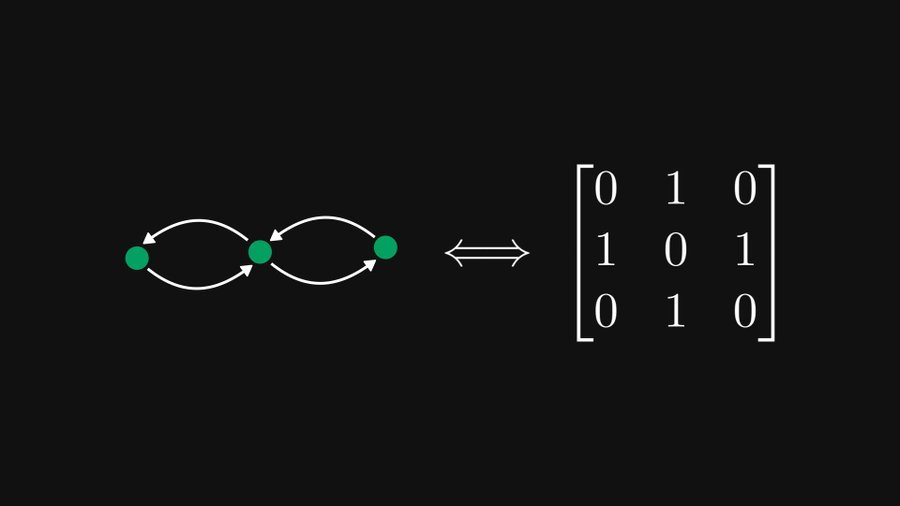
Danka menerangkan dengan contoh. (Demi kesederhanaan, semua pemberat dalam contoh adalah berat unit, tetapi dalam praktiknya nilai berat ini boleh menjadi sebarang nilai bukan negatif.)
Mari kita transkripsikan graf ini yang mengandungi komponen yang bersambung kuat tetapi tidak bersambung kuat sendiri ke dalam bentuk Matriks yang sepadan:
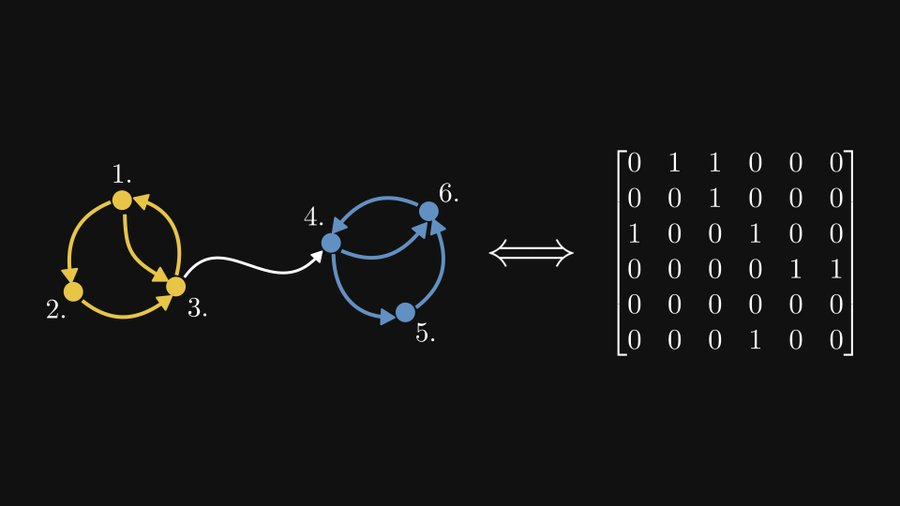
Dan matriks ini adalah matriks boleh dikurangkan.
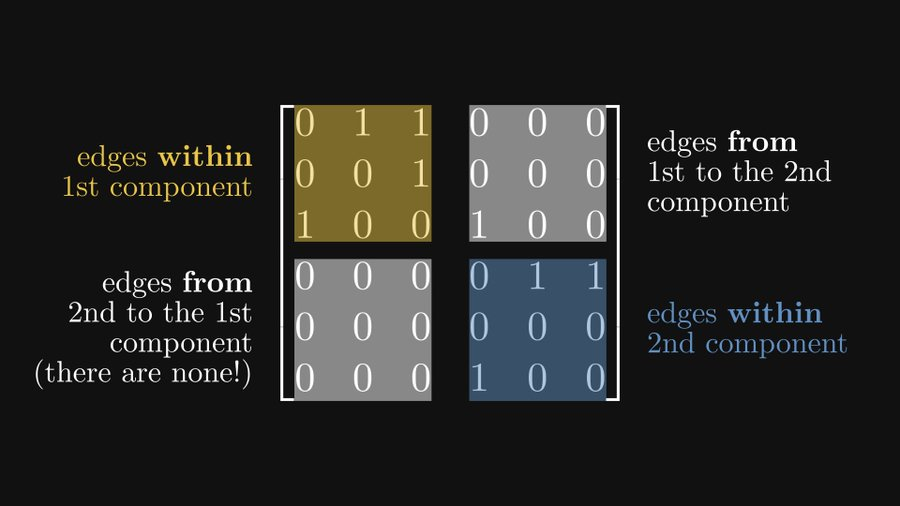
Dapat dilihat bahawa dua submatriks pada pepenjuru utama masing-masing mewakili dua komponen bersambung kuat, dan submatriks di bahagian atas sebelah kanan mewakili tepi daripada komponen pertama bersambung kuat kepada komponen kedua bersambung kuat, satu pada kiri bawah mewakili tepi daripada komponen kedua bersambung kuat ke komponen pertama bersambung kuat (kerana tiada tepi sedemikian, semuanya adalah 0).
Bentuk penulisan matriks blok ini dipanggil Frobenius bentuk normal.

Jadi, kita secara semula jadi bertanya: Bolehkah kita menukar mana-mana matriks bukan negatif kepada matriks bentuk normal Frobenius?
Dengan menggunakan graf terarah untuk mewakili matriks bukan negatif, kita boleh melihat dengan mudah bahawa jawapannya adalah ya, kerana mana-mana graf berarah yang mewakili matriks bukan negatif boleh diwakili sebagai komponen bersambung kuat yang bersambung antara satu sama lain. Proses ini sangat mudah:
Bina graf terarah yang sepadan untuk matriks bukan negatif;
Itu sahaja!
- Gunakan gambar untuk mendapatkan borang standard Frobenius Jadi, apakah cara yang lebih baik ini?
Berdasarkan contoh di atas, mari kita lihat prosesnya.
Mula-mula, satukan setiap komponen yang bersambung kuat menjadi satu objek, seperti yang ditunjukkan dalam rajah di bawah. Pada masa ini, kami boleh menganggap setiap komponen yang bersambung kuat sebagai kotak hitam - kami tidak mengambil berat tentang struktur dalamannya, hanya sambungan luarannya.
Kemudian, dalam graf baharu ini, kita perlu mencari komponen yang hanya mempunyai tepi keluar tetapi tiada tepi masuk. Terdapat hanya satu dalam contoh khusus ini, dan kami melabelkannya nombor 0:Langkah seterusnya adalah lebih menyusahkan: nomborkan setiap komponen supaya nombor setiap komponen adalah jarak paling jauh dari nombor 0. Contoh berikut boleh menggambarkan perkara ini dengan lebih jelas: 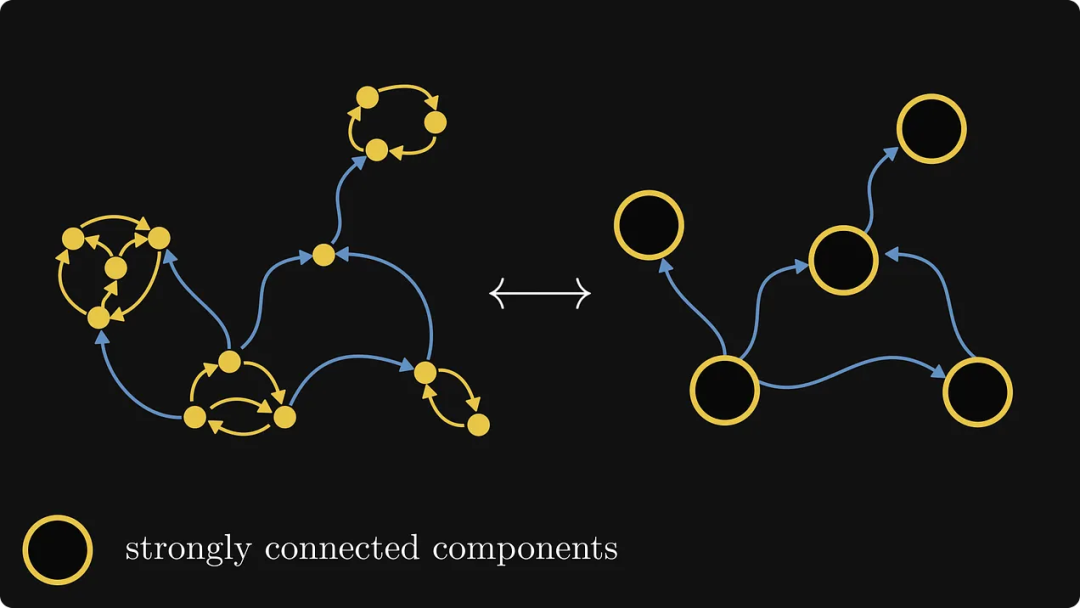
Anda boleh melihat bahawa terdapat dua laluan dari No. 0 ke komponen tengah, jadi pilih laluan paling jauh dari 0 untuk menomborkannya. Akhirnya dapat: 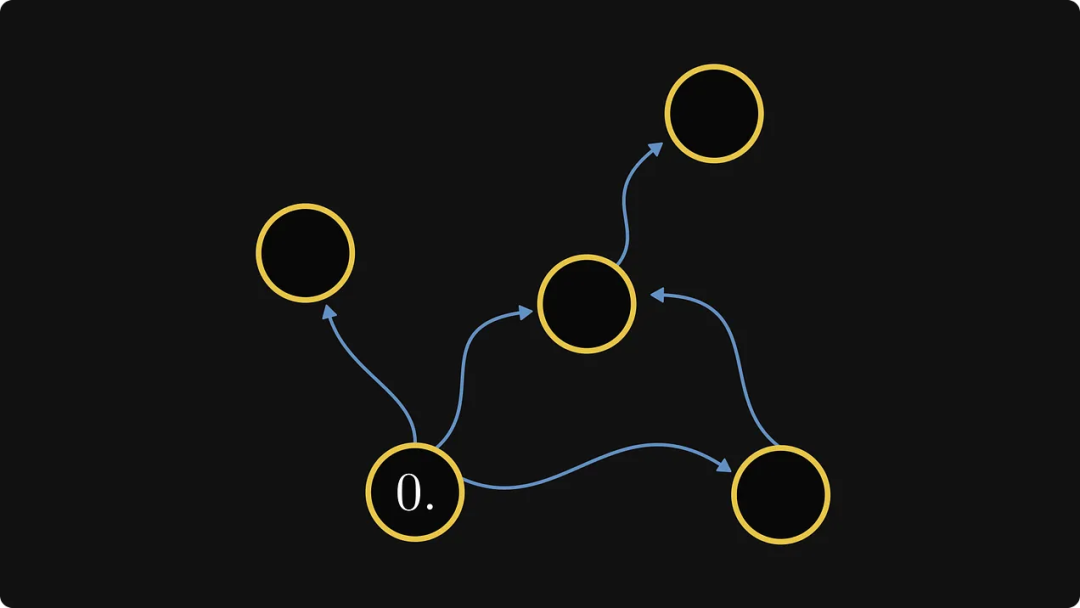
Eigentlich definiert dies die Reihenfolge der Komponenten. Beschriften Sie als Nächstes die internen Knoten jeder Komponente:
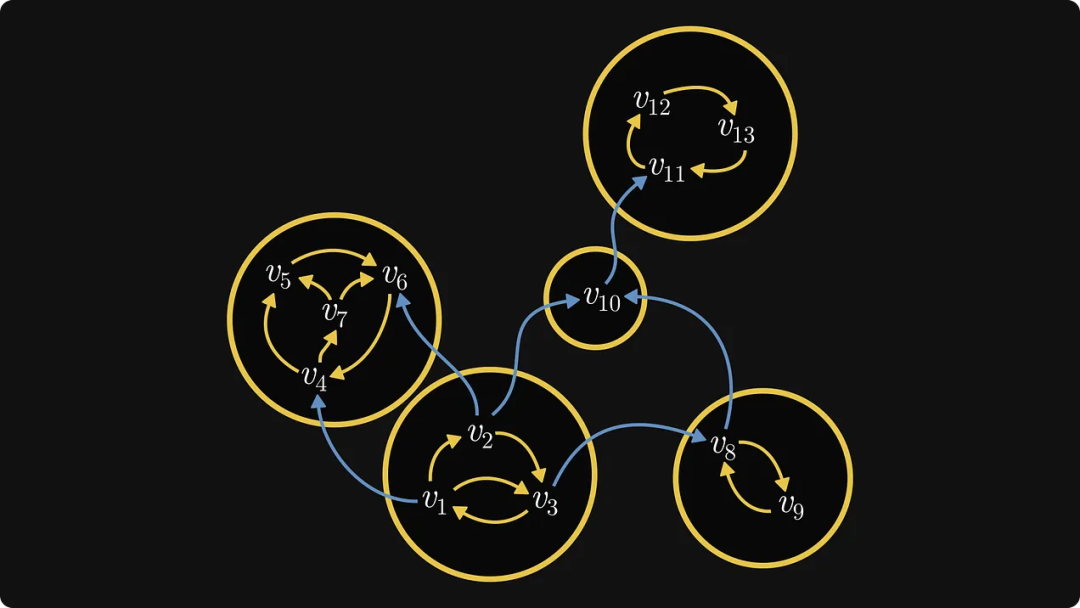
Wenn der Graph selbst aus einer Matrix stammt, kann ein solcher Umbenennungsprozess zu einer kanonischen Frobenius-Matrix führen!

Tatsächlich besteht dieser Neumarkierungsprozess darin, eine Permutationsmatrix P zu verwenden, um die ursprüngliche Matrix zu transformieren, und die Permutationsmatrix besteht aus dem Produkt mehrerer transponierter Matrizen.
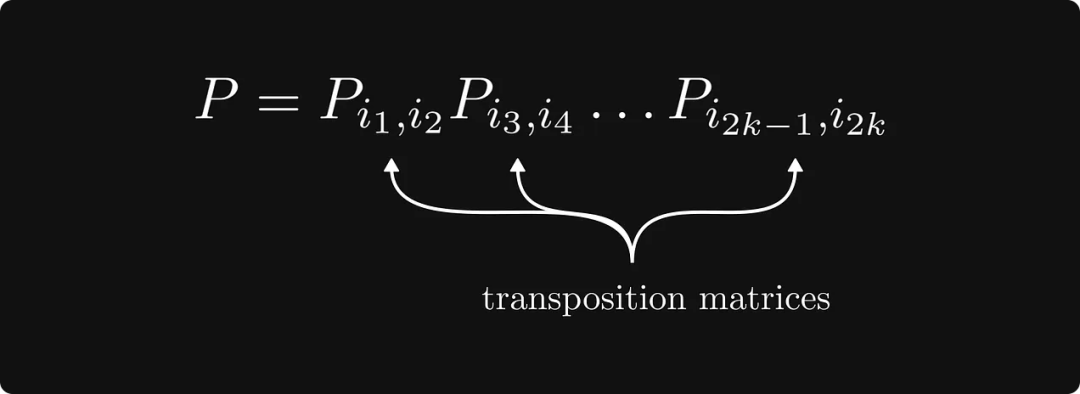
Das Folgende ist die vollständige Form des Satzes:

Natürlich geht die Verwendung von Diagrammen zur Darstellung von Matrizen weit darüber hinaus. Beispielsweise können wir auch die Eigenwerte der Matrix verwenden um die Eigenwerte des Graphen zu definieren. Tatsächlich entstand aus dieser Denkweise das Forschungsgebiet der Spektralgraphentheorie.
Fazit
Offensichtlich ist diese Äquivalenzbeziehung zwischen Matrizen und Graphen nicht nur hilfreich für die Forschung zur Graphentheorie, sondern bietet auch eine neue Perspektive für die Berechnung und Analyse der linearen Algebra. Es hat auch einige wichtige praktische Verwendungsmöglichkeiten. Beispielsweise werden DNA-Daten häufig in Form von Matrizen oder Diagrammen dargestellt.
Darüber hinaus wissen wir alle, wie wichtig Matrixoperationen für die aktuelle KI mit großen Modellen sind, und durch Wissensgraphen dargestellte Diagramme werden durch Technologien wie die abrufgestützte Suche auch zu einem wichtigen Treiber der aktuellen KI. Die Verbindung beider könnte zu neuen Durchbrüchen in der Interpretierbarkeit von KI und der grafischen künstlichen Intelligenz führen. Zumindest hilft uns dies, die lineare Algebra besser zu lernen.
Tatsächlich stammt der obige Inhalt aus dem Buch „Mathematik des maschinellen Lernens“, das von Tivadar Danka geschrieben wurde. In diesem Buch wird das mathematische Wissen im Zusammenhang mit maschinellem Lernen von einer einfachen bis hin zu einer tiefgreifenden Ebene eingeführt, sodass die Leser wirklich verstehen können, was passiert und warum Danka zuversichtlich erklärt, dass dies „die beste Ressource für das Erlernen maschinellen Lernens“ sein wird. Derzeit hat er zwei Kapitelvorschauen online veröffentlicht: https://tivadardanka.com/mathematics-of-machine-learning-preview/
Atas ialah kandungan terperinci Mengapa saya tidak tahu semasa saya belajar penjanaan garis: Terdapat hubungan kesetaraan antara matriks dan graf?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Tutorial Model Penyebaran Bernilai Masa Anda, dari Universiti Purdue
Apr 07, 2024 am 09:01 AM
Tutorial Model Penyebaran Bernilai Masa Anda, dari Universiti Purdue
Apr 07, 2024 am 09:01 AM
Penyebaran bukan sahaja boleh meniru lebih baik, tetapi juga "mencipta". Model resapan (DiffusionModel) ialah model penjanaan imej. Berbanding dengan algoritma yang terkenal seperti GAN dan VAE dalam bidang AI, model resapan mengambil pendekatan yang berbeza. Idea utamanya ialah proses menambah hingar pada imej dan kemudian secara beransur-ansur menolaknya. Cara mengecilkan dan memulihkan imej asal adalah bahagian teras algoritma. Algoritma akhir mampu menghasilkan imej daripada imej bising rawak. Dalam beberapa tahun kebelakangan ini, pertumbuhan luar biasa AI generatif telah membolehkan banyak aplikasi menarik dalam penjanaan teks ke imej, penjanaan video dan banyak lagi. Prinsip asas di sebalik alat generatif ini ialah konsep resapan, mekanisme pensampelan khas yang mengatasi batasan kaedah sebelumnya.
 Hasilkan PPT dengan satu klik! Kimi: Biarlah 'pekerja migran PPT' menjadi popular dahulu
Aug 01, 2024 pm 03:28 PM
Hasilkan PPT dengan satu klik! Kimi: Biarlah 'pekerja migran PPT' menjadi popular dahulu
Aug 01, 2024 pm 03:28 PM
Kimi: Hanya dalam satu ayat, dalam sepuluh saat sahaja, PPT akan siap. PPT sangat menjengkelkan! Untuk mengadakan mesyuarat, anda perlu mempunyai PPT; untuk menulis laporan mingguan, anda perlu mempunyai PPT untuk membuat pelaburan, anda perlu menunjukkan PPT walaupun anda menuduh seseorang menipu, anda perlu menghantar PPT. Kolej lebih seperti belajar jurusan PPT Anda menonton PPT di dalam kelas dan melakukan PPT selepas kelas. Mungkin, apabila Dennis Austin mencipta PPT 37 tahun lalu, dia tidak menyangka satu hari nanti PPT akan berleluasa. Bercakap tentang pengalaman sukar kami membuat PPT membuatkan kami menitiskan air mata. "Ia mengambil masa tiga bulan untuk membuat PPT lebih daripada 20 muka surat, dan saya menyemaknya berpuluh-puluh kali. Saya rasa ingin muntah apabila saya melihat PPT itu." ialah PPT." Jika anda mengadakan mesyuarat dadakan, anda harus melakukannya
 Semua anugerah CVPR 2024 diumumkan! Hampir 10,000 orang menghadiri persidangan itu di luar talian dan seorang penyelidik Cina dari Google memenangi anugerah kertas terbaik
Jun 20, 2024 pm 05:43 PM
Semua anugerah CVPR 2024 diumumkan! Hampir 10,000 orang menghadiri persidangan itu di luar talian dan seorang penyelidik Cina dari Google memenangi anugerah kertas terbaik
Jun 20, 2024 pm 05:43 PM
Pada awal pagi 20 Jun, waktu Beijing, CVPR2024, persidangan penglihatan komputer antarabangsa teratas yang diadakan di Seattle, secara rasmi mengumumkan kertas kerja terbaik dan anugerah lain. Pada tahun ini, sebanyak 10 kertas memenangi anugerah, termasuk 2 kertas terbaik dan 2 kertas pelajar terbaik Selain itu, terdapat 2 pencalonan kertas terbaik dan 4 pencalonan kertas pelajar terbaik. Persidangan teratas dalam bidang visi komputer (CV) ialah CVPR, yang menarik sejumlah besar institusi penyelidikan dan universiti setiap tahun. Mengikut statistik, sebanyak 11,532 kertas telah diserahkan tahun ini, 2,719 daripadanya diterima, dengan kadar penerimaan 23.6%. Menurut analisis statistik data CVPR2024 Institut Teknologi Georgia, dari perspektif topik penyelidikan, bilangan kertas terbesar ialah sintesis dan penjanaan imej dan video (Imageandvideosyn
 Lima perisian pengaturcaraan untuk memulakan pembelajaran bahasa C
Feb 19, 2024 pm 04:51 PM
Lima perisian pengaturcaraan untuk memulakan pembelajaran bahasa C
Feb 19, 2024 pm 04:51 PM
Sebagai bahasa pengaturcaraan yang digunakan secara meluas, bahasa C merupakan salah satu bahasa asas yang mesti dipelajari bagi mereka yang ingin melibatkan diri dalam pengaturcaraan komputer. Walau bagaimanapun, bagi pemula, mempelajari bahasa pengaturcaraan baharu boleh menjadi sukar, terutamanya disebabkan kekurangan alat pembelajaran dan bahan pengajaran yang berkaitan. Dalam artikel ini, saya akan memperkenalkan lima perisian pengaturcaraan untuk membantu pemula memulakan bahasa C dan membantu anda bermula dengan cepat. Perisian pengaturcaraan pertama ialah Code::Blocks. Code::Blocks ialah persekitaran pembangunan bersepadu sumber terbuka (IDE) percuma untuk
 Panduan Pemasangan PyCharm Edisi Komuniti: Kuasai semua langkah dengan cepat
Jan 27, 2024 am 09:10 AM
Panduan Pemasangan PyCharm Edisi Komuniti: Kuasai semua langkah dengan cepat
Jan 27, 2024 am 09:10 AM
Mula Pantas dengan PyCharm Edisi Komuniti: Tutorial Pemasangan Terperinci Analisis Penuh Pengenalan: PyCharm ialah persekitaran pembangunan bersepadu (IDE) Python yang berkuasa yang menyediakan set alat yang komprehensif untuk membantu pembangun menulis kod Python dengan lebih cekap. Artikel ini akan memperkenalkan secara terperinci cara memasang Edisi Komuniti PyCharm dan menyediakan contoh kod khusus untuk membantu pemula bermula dengan cepat. Langkah 1: Muat turun dan pasang Edisi Komuniti PyCharm Untuk menggunakan PyCharm, anda perlu memuat turunnya dari tapak web rasminya terlebih dahulu
 Mesti dibaca untuk pemula teknikal: Analisis tahap kesukaran bahasa C dan Python
Mar 22, 2024 am 10:21 AM
Mesti dibaca untuk pemula teknikal: Analisis tahap kesukaran bahasa C dan Python
Mar 22, 2024 am 10:21 AM
Tajuk: Wajib dibaca untuk pemula teknikal: Analisis kesukaran bahasa C dan Python, memerlukan contoh kod khusus Dalam era digital hari ini, teknologi pengaturcaraan telah menjadi keupayaan yang semakin penting. Sama ada anda ingin bekerja dalam bidang seperti pembangunan perisian, analisis data, kecerdasan buatan, atau hanya belajar pengaturcaraan kerana minat, memilih bahasa pengaturcaraan yang sesuai ialah langkah pertama. Di antara banyak bahasa pengaturcaraan, bahasa C dan Python adalah dua bahasa pengaturcaraan yang digunakan secara meluas, masing-masing mempunyai ciri tersendiri. Artikel ini akan menganalisis tahap kesukaran bahasa C dan Python
 Daripada logam kosong kepada model besar dengan 70 bilion parameter, berikut ialah tutorial dan skrip sedia untuk digunakan
Jul 24, 2024 pm 08:13 PM
Daripada logam kosong kepada model besar dengan 70 bilion parameter, berikut ialah tutorial dan skrip sedia untuk digunakan
Jul 24, 2024 pm 08:13 PM
Kami tahu bahawa LLM dilatih pada kelompok komputer berskala besar menggunakan data besar-besaran Tapak ini telah memperkenalkan banyak kaedah dan teknologi yang digunakan untuk membantu dan menambah baik proses latihan LLM. Hari ini, perkara yang ingin kami kongsikan ialah artikel yang mendalami teknologi asas dan memperkenalkan cara menukar sekumpulan "logam kosong" tanpa sistem pengendalian pun menjadi gugusan komputer untuk latihan LLM. Artikel ini datang daripada Imbue, sebuah permulaan AI yang berusaha untuk mencapai kecerdasan am dengan memahami cara mesin berfikir. Sudah tentu, mengubah sekumpulan "logam kosong" tanpa sistem pengendalian menjadi gugusan komputer untuk latihan LLM bukanlah proses yang mudah, penuh dengan penerokaan dan percubaan dan kesilapan, tetapi Imbue akhirnya berjaya melatih LLM dengan 70 bilion parameter proses terkumpul
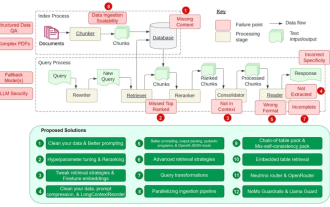 Mengira 12 titik kesakitan RAG, arkitek kanan NVIDIA mengajar penyelesaian
Jul 11, 2024 pm 01:53 PM
Mengira 12 titik kesakitan RAG, arkitek kanan NVIDIA mengajar penyelesaian
Jul 11, 2024 pm 01:53 PM
Retrieval-augmented generation (RAG) ialah teknik yang menggunakan perolehan semula untuk meningkatkan model bahasa. Secara khusus, sebelum model bahasa menjana jawapan, ia mendapatkan semula maklumat yang berkaitan daripada pangkalan data dokumen yang luas dan kemudian menggunakan maklumat ini untuk membimbing proses penjanaan. Teknologi ini boleh meningkatkan ketepatan dan perkaitan kandungan dengan banyak, mengurangkan masalah halusinasi dengan berkesan, meningkatkan kelajuan kemas kini pengetahuan, dan meningkatkan kebolehkesanan penjanaan kandungan. RAG sudah pasti salah satu bidang penyelidikan kecerdasan buatan yang paling menarik. Untuk butiran lanjut tentang RAG, sila rujuk artikel lajur di tapak ini "Apakah perkembangan baharu dalam RAG, yang pakar dalam menebus kekurangan model besar?" Ulasan ini menerangkannya dengan jelas." Tetapi RAG tidak sempurna, dan pengguna sering menghadapi beberapa "titik kesakitan" apabila menggunakannya. Baru-baru ini, penyelesaian AI generatif termaju NVIDIA






