

Dalam dunia kewangan yang pantas, ketepatan adalah segala-galanya. Adalah lebih baik untuk mengelak kerugian jutaan$ kerana ralat pembulatan / ketepatan.
Titik permulaan artikel ini ialah kesedaran bahawa wang bukanlah purata nombor asas anda yang boleh anda gunakan untuk mengira epal dalam bakul anda. Apa yang anda dapat apabila anda cuba mendarab 10€ dengan 10$? Sukar huh... Pernahkah anda menjumpai $1.546 yang ajaib di dalam poket jaket lama? Ya saya tahu, ini juga tidak mungkin. Contoh-contoh bodoh ini ada di sini untuk menggambarkan hakikat bahawa wang mempunyai peraturan tersendiri dan bukan sahaja boleh dimodelkan dengan nombor mudah. Saya meyakinkan anda, saya bukan orang pertama yang menyedarinya (dan mungkin anda menyedarinya jauh sebelum saya). Pada tahun 2002, pengaturcara Martin Fowler mencadangkan dalam Corak Seni Bina Aplikasi Perusahaan cara untuk mewakili wang, dengan atribut dan peraturan operan khusus. Baginya, dua atribut berdaya maju minimum yang diperlukan untuk jenis data wang ialah:
amount currency
Perwakilan yang sangat asas ini akan menjadi titik permulaan kami untuk membina model kewangan yang mudah tetapi teguh.
Jumlah wang pastinya merupakan nombor tertentu: ia mempunyai ketepatan tetap (sekali lagi, anda tidak boleh mempunyai 4.376$ dalam poket anda). Anda perlu memilih cara untuk mewakilinya yang membantu anda untuk menghormati kekangan ini.
Amaran spoiler, ini pastinya bukan idea yang baik jika anda tidak mahu melihat beberapa sen (jika bukan dolar) hilang dalam dunia gelap perwakilan nombor titik terapung.
Jika anda mempunyai sedikit pengalaman dengan pengekodan dalam JavaScript, anda tahu bahawa pengiraan yang paling mudah sekalipun boleh mengakibatkan ralat ketepatan yang tidak anda jangkakan pada mulanya. Contoh yang paling jelas dan terkenal untuk menyerlahkan fenomena ini ialah:
0.1 + 0.2 !== 0.3 // true 0.1 + 0.2 // 0.30000000000000004
Jika contoh ini tidak meyakinkan anda sepenuhnya, saya nasihatkan anda untuk melihat artikel ini yang menyelam lebih jauh ke dalam semua hasil pengiraan bermasalah yang boleh anda hadapi semasa menggunakan jenis nombor asli JavaScript…
Delta kecil dalam keputusan ini mungkin kelihatan tidak berbahaya kepada anda (dengan magnitud kira-kira ~ 10^-16), namun dalam aplikasi kewangan yang kritikal, ralat sedemikian boleh melata dengan cepat. Pertimbangkan untuk memindahkan dana antara beribu-ribu akaun, di mana setiap transaksi melibatkan pengiraan yang serupa. Sedikit ketidaktepatan bertambah, dan sebelum anda mengetahuinya, penyata kewangan anda dikurangkan sebanyak beribu-ribu dolar. Dan secara jujur, kita semua boleh bersetuju bahawa apabila ia berkaitan dengan wang, kesilapan tidak dibenarkan: dari segi undang-undang dan untuk membina hubungan yang boleh dipercayai dengan pelanggan anda.
Soalan pertama yang saya tanya pada diri sendiri apabila menghadapi isu dalam salah satu projek saya ialah mengapa ? Saya mendapati bahawa punca masalahnya bukan JavaScript dan ketidaktepatan ini turut mempengaruhi bahasa pengaturcaraan moden yang lain (Java, C, Python, …).
// In C
#include <stdio.h>
int main() {
double a = 0.1;
double b = 0.2;
double sum = a + b;
if (sum == 0.3) {
printf("Equal\n");
} else {
printf("Not Equal\n"); // This block is executed
}
return 0;
}
// > Not equal
// In Java
public class doublePrecision {
public static void main(String[] args) {
double total = 0;
total += 5.6;
total += 5.8;
System.out.println(total);
}
}
// > 11.399999999999
Malah, punca utamanya terletak pada standard yang digunakan oleh bahasa ini untuk mewakili nombor titik terapung : format titik terapung berketepatan dua (atau tunggal), yang ditentukan oleh piawaian IEEE 754.
Dalam Javascript, nombor jenis asli sepadan dengan nombor titik terapung berketepatan ganda, yang bermaksud bahawa nombor dikodkan dengan 64 bit dan dibahagikan kepada tiga bahagian:
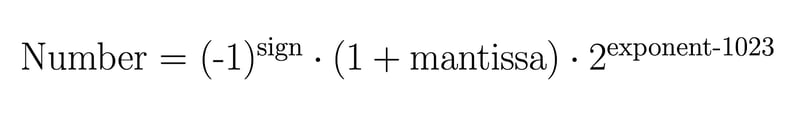
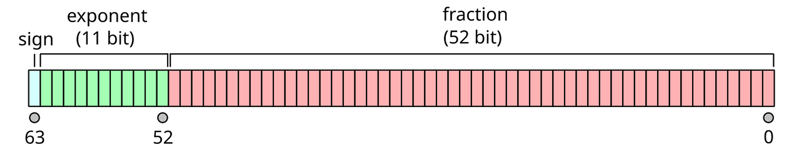
Kemudian, anda perlu menggunakan formula berikut untuk menukar perwakilan bit anda kepada nilai perpuluhan:
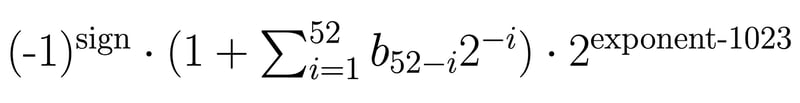
Contoh perwakilan nombor titik terapung berketepatan dua, anggaran 1/3 :
0 01111111101 0101010101010101010101010101010101010101010101010101 = (-1)^0 x (1 + 2^-2 + 2^-4 + 2^-6 + ... + 2^-50 + 2^-52) x 2^(1021-1023) = 0.333333333333333314829616256247390992939472198486328125 ~ 1/3
This format allows us to represent a vast range of values, but it can't represent every possible number with absolute precision (just between 0 and 1 you can find an infinity of numbers…). Many numbers cannot be represented exactly in binary form. To loop on the first example, that's the issue with 0.1 and 0.2. Double-point floating representation gives us an approximation of these value, so when you add these two imprecise representations, the result is also not exact.
Now that you are fully convinced that handling money amounts with native JavaScript number type is a bad idea (at least I hope you begin to have doubts about it), the 1Billion$ question is how should you proceed ? A solution could be to make use of some of the powerful fixed-precision arithmetic packages available in JavaScript. For example Decimal.js (which is used by the popular ORM Prisma to represent its Decimal datatype) or Big.js.
These packages provide you with special datatypes that allow you to perform calculations with getting rid of precision errors we explained above.
// Example using Decimal.js
const Decimal = require('decimal.js');
const a = new Decimal('0.1');
const b = new Decimal('0.2');
const result = a.plus(b);
console.log(result.toString()); // Output: '0.3'
This approach provides you with another advantage, it drastically extends the maximum value that can be represented, which can become pretty handy when you are dealing with cryptocurrencies for example.
Even if it is really robust, that it not the one I prefer to choose to implement in my web applications. I find it easier and clearer to apply Stripe strategy to only deal with integer values.
We, at Theodo Fintech, value pragmatism! We love to take inspiration from the most succeeding companies in the industry. Stripe, the well-known billions$ company specialized in payment services, made the choice to handle money amounts without floating numbers but with integers. To do that, they use the smallest unit of the currency to represent a monetary amount.
// 10 USD are represented by
{
"amount": 1000,
"currency": "USD"
}
I guess that many of you already know this: all currencies don't have the smallest unit of the same magnitude. Most of them are "two-decimal" currencies (EUR, USD, GBP) which means that their smallest unit is 1/100th of the currency. However, some are "three-decimal" currencies (KWD) or even "zero-decimal" currencies (JPY). (You can find more information about it by following the ISO4217 standard). To handle these disparities, you should integrate to your money data representation the multiplicative factor to convert an amount represented in the smallest unit into the corresponding currency.
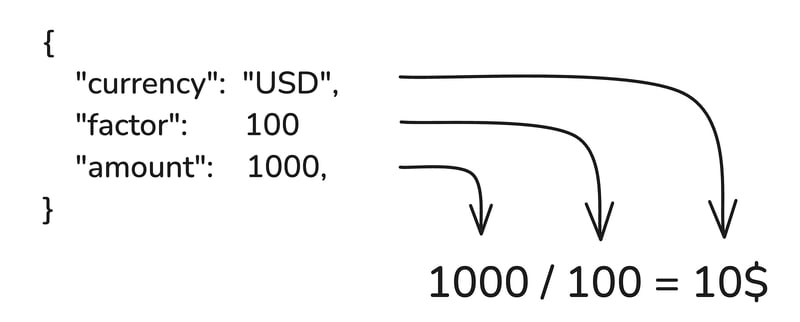
I guess you already figured it out, you can either work with native number , third party arbitrary-precision packages or integers, calculations can (and will) lead you to floating-point results that you will need to round to your monetary finite precision. As a quick example is never to much, let's say that you handle integer values and contracted a loan of 16k$ with a really precise interest rate of 8.5413% (ouch…). You then need to refund 16k$ plus an additional amount of
1600000 * 0.085413 // amount in cents //Output in cents: 136660.8
The crux is to properly handle the rounding process of money amounts after calculations. Most of the time, you end up having to choose between three different kinds of rounding:
When it comes to roundings, there is not really any "magic sauce": you need to arbitrate depending on your situation. I recommend you always check legislation when you deal with a new currency and a new rounding use case (conversion, money split, interest rates for credits, …). You better follow regulations right away to avoid further troubles. For example, when it comes to conversion rates, most currencies have determined rules about needed precision and rounding rules (you can have a look at the EUR conversion rate rules here).
Artikel ini tidak menyeluruh tentang semua kemungkinan sedia ada untuk mengendalikan jumlah wang dalam JavaScript dan juga tidak bertujuan untuk memberi anda model data wang yang lengkap/sempurna. Saya cuba memberi anda petunjuk dan garis panduan yang mencukupi untuk melaksanakan perwakilan yang terbukti konsisten, berdaya tahan dan dipilih oleh pelakon besar industri fintech. Saya berharap anda akan dapat melakukan pengiraan jumlah wang dalam projek masa depan anda tanpa melupakan sebarang sen di dalam poket anda (jika tidak, jangan lupa untuk melihat jaket lama anda)!
Atas ialah kandungan terperinci Ketepatan Kewangan dalam JavaScript: Mengendalikan Wang Tanpa Kehilangan Sen. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




