c语言 三种求回文数的算法

今天小编和大家分享的文章是c语言的三种描述回文数的算法，具有一定参考价值，对C语言回文数有兴趣的可以来看看，希望对你有所帮助。

题目描述

• 注意：（这些回文数都没有前导0）
• 1位的回文数有0，1，2，3，4，5，6，7，8，9   共10个；
• 2位的回文数有11，22，33，44，55，66，77，88，99  共9个；

*　请问：n位的回文数有多少个？请编写一个递归函数来解决此问题！！！

• 【输入形式】一行一个正整数，代表多少位
• 【输出形式】一行一个正整数，代表回文诗的个数
• 【样例输入】2
• 【样例输出】9

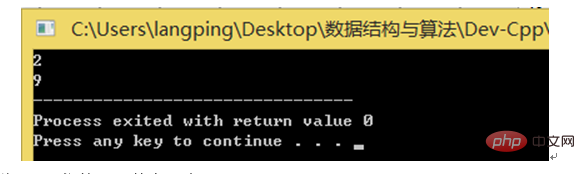
输入：
3
输出：
90

输入：
5
输出：
900

**输入：
10
输出：
90000**

输入：
8
输出：
9000

输入：
1
输出：
10

思路分析

1. 通过for循环读入这个数,通过/和%操作将这个数据逆转,然后再对比逆转后的数字是否和原数字相等

2. 

3. 通过for循环读入这个数,每次取头位一个数字和末位一个数字,依次比较这两个数字是否相等,再去掉这两个数字,直到剩下一个数字(位数为奇数)或者剩下两个数字(位数为偶数)

4. 

5. 通过数学关系,直接判断位数,算出这个位数内的回文数个数;

   • 例如:99899
   • 可以把它分为两半,取前面一半998,如果是回文数,其后面一半一定是与其相应位置对应,998为3位数
     字,**除第一位(不包含前导0)故与后半对应的位置那个数有9种选择(1-9)外,其他位都与相应的位置有10种
     选择(0-9)**,例如第二位和倒数第二位(0-9)
   • 所以可以总结出来相同的位数,位数为奇数奇数其回文数有9*10^(n/2)个,注意n/2是整数,位数为偶数的为
     910^(n/2-1)个,所以5位数字的的回文数有910*10=900个
   • 注意位数为1有10个(0-9),需要特殊处理

相关教程：C视频教程

代码描述

1. 第一种思路:

#include <stdio.h>
#include <math.h>
int reverse(long int i,long int *terminate)        //递归函数求数值的逆序
{
    if (i<=0){              //递归出口
        return 1;       
    }
    else{
        *terminate*=10;     //每次乘10升位数
        *terminate+=i%10;      //加上个位
        reverse(i/10,terminate);        //递归每次规模缩小
    }
    return 1;
}
int main ()
{
    int n;
    scanf ("%d",&n);            //读入一个n,表示n位整数
   long int i;        
    int count=0;
    if (n==1){               //如果等于1,则有10个(0-9都是),特殊处理;
        printf ("10");
        return 0;
    }
    for (i=pow(10,n-1);i<pow(10,n);i++){       //从第一个n位数开始(10^(n-1)),到(10^n)-1
       long int terminate=0;                //定义一个逆序目标数
        reverse(i,&terminate);              //把i和逆序目标数传入
        if (terminate==i){                  //逆序后还和原数相等,则可计数
            count++;
        }
    }
    printf ("%d",count);        //输出个数
    return 0;
}

2. 第二种思路:

#include <stdio.h>
#include <math.h>
int judge(int i,int n)
{
    int first,last;
    if (n<=1){          //规模减小,直到n为1(偶数)或者0
        return 1;

    }
    else{
        first=i/pow(10,n-1);        //头位数字
        last=i%10;                  //末位数字
        if (first!=last){           //头位末尾不一样直接退出
            return 0;
        }
        int tem=pow(10,n-1);        
    judge(i%tem/10,n-2);            //剔除头尾剩下中间,位数减二

    }
}
int main ()
{
    int n;
    scanf("%d",&n);
    if (1==n){
        printf ("10");
        return 0;
    }
    int i;
    int count=0;
   long long  low=pow(10,n-1);      //循环入口
    long long high=pow(10,n);       //循环出口
    for (i=low;i<high;i++){
       if ( judge(i,n)==1){         //判断i是否为回文,计数
           count++;
       }
    }
    printf ("%d",count);
    return 0;
}

3. 第三种思路:

#include <stdio.h>
#include <math.h>
int main (){
    int n;
    scanf ("%d",&n);
    int ji=9*pow(10,n/2),ou=9*pow(10,n/2-1);
    if (n==1){
        printf ("10");
    }
    else if  (n==2){
        printf ("%d",9);
    }
    else if (n%2==1){
        printf ("%d",ji);
    }
    else if (n%2==0){
        printf("%d",ou);
    }
    return 0;
}

Atas ialah kandungan terperinci c语言 三种求回文数的算法. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!