Maison >développement back-end >Tutoriel Python >Comment implémenter un analyseur de descente récursive en Python
Pour analyser ce type de texte, une autre règle de grammaire spécifique est requise. Nous introduisons ici les règles grammaticales Backus Normal Form (BNF) et Extended Backus Normal Form (EBNF) qui peuvent représenter une grammaire sans contexte. Qu'ils soient aussi petits qu'une expression d'opération arithmétique ou aussi grands que presque tous les langages de programmation, ils sont définis à l'aide de grammaires sans contexte.
Pour des expressions arithmétiques simples, supposons que nous avons utilisé la technologie de segmentation de mots pour le convertir en un flux de jetons d'entrée, tel que NUM+NUM*NUM (voir le billet de blog précédent pour la méthode de segmentation de mots) . NUM+NUM*NUM（分词方法参见上一篇博文）。
在此基础上，我们定义BNF规则定义如下：
expr ::= expr + term
| expr - term
| term
term ::= term * factor
| term / factor
| factor
factor ::= (expr)
| NUM当然，这种计法还不够简洁明了，我们实际采用的为EBNF形式：
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUMBNF和EBNF每一条规则(形如::=的式子)都可以看做是一种替换，即左侧的符号可以被右侧的符号所替换。我们在解析过程中尝试使用BNF/EBNF将输入文本与语法规则进行匹配，以完成各种替换和扩展。在EBNF中，被放置在{...}*内的规则是可选的，而*则表示可以重复零次或多次（类比于正则表达式）。
下图形象地展示了递归下降解析器(parser)中“递归”和“下降”部分和ENBF的关系：
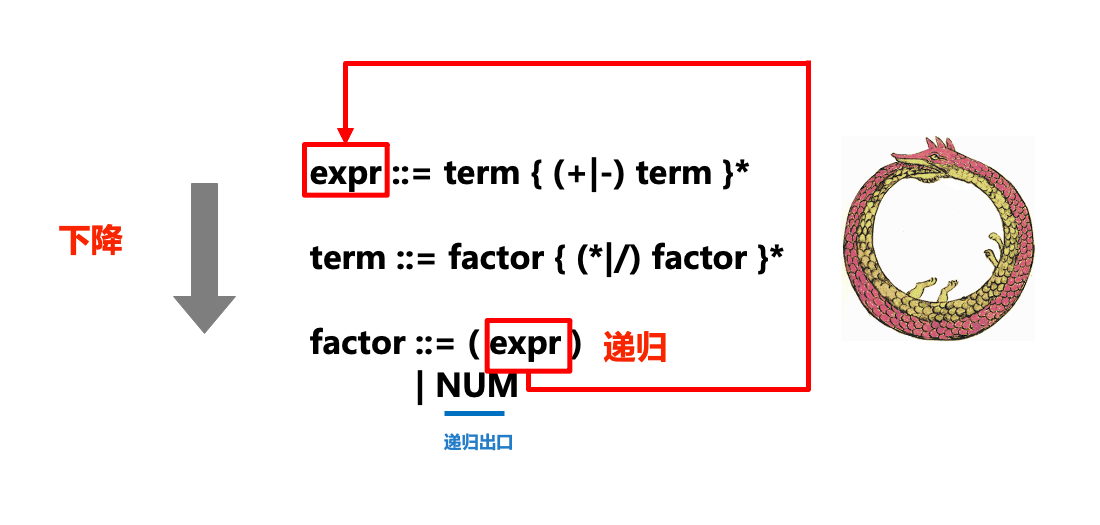
在实际的解析过程中，我们对tokens流从左到右进行扫描，在扫描的过程中处理token，如果卡住就产生一个语法错误。每一条语法规则都被转化为一个函数或方法，例如上面的ENBF规则被转换成下述方法：
class ExpressionEvaluator():
...
def expr(self):
...
def term(self):
...
def factor(self):
...在调用某个规则对应方法的过程中，如果我们发现接下来的符号需要采用另一个规则来匹配，则我们就会“下降”到另一个规则方法（如在expr中调用term，term中调用factor），则也就是递归下降中“下降”的部分。
有时也会调用已经在执行的方法（比如在expr中调用term，term中调用factor后，又在factor中调用expr，相当于一条衔尾蛇），这也就是递归下降中“递归”的部分。
对于语法中出现的重复部分（例如expr ::= term { (+|-) term }*），我们则通过while循环来实现。
下面我们来看具体的代码实现。首先是分词部分，我们参照上一篇介绍分词博客的代码。
import re
import collections
# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配数字，+表示任意长度
PLUS = r'(?P<PLUS>\+)' # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意转义
RPAREN = r'(?P<RPAREN>\))' # 注意转义
WS = r'(?P<WS>\s+)' # 别忘记空格，\s表示空格，+表示任意长度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 过滤掉空格符
yield tok下面是表达式求值器的具体实现：
class ExpressionEvaluator():
""" 递归下降的Parser实现，每个语法规则都对应一个方法，
使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
"""
def parse(self, text):
""" 对外调用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一个token，下一个即将匹配的token
self._next() # 转到下一个token
return self.expr() # 开始递归
def _next(self):
""" 转到下一个token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一个token与tok_type匹配，则转到下一个token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 检查是否匹配，如果不匹配则抛出异常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下来是语法规则，每个语法规则对应一个方法
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")我们输入以下表达式进行测试：
e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))求值结果如下：
2
5
14
37
如果我们输入的文本不符合语法规则：
print(e.parse("2 + (3 + * 4)"))则会抛出SyntaxError异常：Expected NUMBER or LPAREN。
综上，可见我们的表达式求值算法运行正确。
上面我们是得到表达式的结果，但是如果我们想分析表达式的结构，生成一棵简单的表达式解析树呢？那么我们需要对上述类的方法做一定修改：
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value) # 字符串转整形
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")输入下列表达式测试一下：
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))以下是生成结果：
('+', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
('+', ('+', 2, 3), 4)
可以看到表达式树生成正确。
我们上面的这个例子非常简单，但递归下降的解析器也可以用来实现相当复杂的解析器，例如Python代码就是通过一个递归下降解析器解析的。您要是对此跟感兴趣可以检查Python源码中的Grammar文件来一探究竟。然而，下面我们接着会看到，自己动手写一个解析器会面对各种陷阱和挑战。
任何涉及左递归形式的语法规则，都没法用递归下降parser来解决。所谓左递归，即规则式子右侧最左边的符号是规则头，比如对于以下规则：
items ::= items ',' item
| item完成该解析你可能会定义以下方法：
def items(self):
itemsval = self.items() # 取第一项，然而此处会无穷递归！
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]这样做会在第一行就无穷地调用self.items()
expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUMBien sûr, cette méthode n'est pas assez concise et claire. Ce que nous utilisons en réalité est la forme EBNF : rrreee
Chaque règle de BNF et EBNF (dans le form:: =) peut être considéré comme une sorte de substitution, c'est-à-dire que le symbole de gauche peut être remplacé par le symbole de droite. Nous essayons d'utiliser BNF/EBNF pour faire correspondre le texte saisi avec les règles de grammaire pendant le processus d'analyse afin d'effectuer diverses substitutions et extensions. Dans EBNF, les règles placées entre {...}* sont facultatives et * indique qu'elles peuvent être répétées zéro ou plusieurs fois (analogue aux expressions régulières). La figure suivante montre de manière frappante la relation entre les parties « récursion » et « descente » de l'analyseur de descente récursive (analyseur) et ENBF : 🎜🎜
🎜🎜Dans le processus d'analyse lui-même, nous analysons le flux de jetons de gauche à droite et traitons les jetons pendant l'analyse processus. S’il reste bloqué, une erreur de syntaxe se produit. Chaque règle de grammaire est convertie en fonction ou méthode. Par exemple, la règle ENBF ci-dessus est convertie en la méthode suivante : 🎜rrreee🎜En cours d'appel de la méthode correspondant à une certaine règle, si nous constatons que le symbole suivant doit le faire. en utiliser une autre Si la règle correspond, nous "descendrons" vers une autre méthode de règle (comme appeler term in expr et factor in term), qui est la partie "descendante" de la descente récursive. 🎜🎜Parfois, des méthodes déjà en cours d'exécution sont appelées (comme appeler term in expr, appeler factor in term, puis appeler expr in factor, ce qui équivaut à un ouroboros. C'est la partie "récursive" de la descente récursive). . 🎜🎜Pour les parties répétées qui apparaissent dans la grammaire (telles que expr ::= term { (+|-) term }*), nous l'implémentons via une boucle while. 🎜🎜Jetons un coup d'œil à l'implémentation spécifique du code. La première est la partie segmentation de mots. Renvoyons-nous à l'article précédent pour présenter le code du blog de segmentation de mots. 🎜rrreee🎜Ce qui suit est l'implémentation spécifique de l'évaluateur d'expression : 🎜rrreee🎜Nous saisissons l'expression suivante pour tester : 🎜rrreee🎜Le résultat de l'évaluation est le suivant : 🎜🎜2🎜Si le texte que nous saisissons n'est pas conforme aux règles grammaticales : 🎜rrreee🎜, une exception SyntaxError sera levée :
5
1437🎜
Nombre attendu ou LPAREN. 🎜('+', 2, 3)🎜Vous pouvez voir que l'arbre d'expression est généré correctement. 🎜🎜 Notre exemple ci-dessus est très simple, mais l'analyseur de descente récursive peut également être utilisé pour implémenter des analyseurs assez complexes. Par exemple, le code Python est analysé via un analyseur de descente récursive. Si cela vous intéresse, vous pouvez consulter le fichier
(' +', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
(' +', ('+', 2, 3), 4)🎜
Grammar dans le code source Python pour le savoir. Cependant, comme nous le verrons ci-dessous, écrire soi-même un analyseur comporte divers pièges et défis. 🎜self.items()Cela entraînera une erreur de récursion infinie. 🎜🎜Il y a également une erreur dans les règles de grammaire elles-mêmes, comme la priorité des opérateurs. Si nous ignorons la priorité des opérateurs et simplifions directement l'expression comme suit : 🎜rrreee🎜PYTHON Copie plein écran🎜🎜Cette syntaxe peut être techniquement implémentée, mais la convention d'ordre de calcul n'est pas suivie, ce qui donne le résultat du calcul de "3+4* 5" soit 35, au lieu des 23 attendus. Par conséquent, des règles d'expression et de durée distinctes sont nécessaires pour garantir l'exactitude des résultats du calcul. 🎜Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!