Home >Backend Development >Python Tutorial >Detailed explanation of edit distance in Python text similarity calculation
Edit Distance
Edit Distance, also known as Levenshtein distance, refers to the minimum number of editing operations required between two strings to convert one into the other. Editing operations include replacing one character with another, inserting a character, and deleting a character. Generally speaking, the smaller the edit distance, the greater the similarity between two strings.
For example, convert the word kitten into sitting: (The edit distance between 'kitten' and 'sitting' is 3)
sitten (k→s)
sittin (e→i)
sitting (→g)
The Levenshtein package in Python can easily calculate the edit distance
Installation of the package: pip install python-Levenshtein<br>
Let’s use it:
# -*- coding:utf-8 -*- import Levenshtein texta = '艾伦 图灵传' textb = '艾伦•图灵传' print Levenshtein.distance(texta,textb)
The execution result of the above program is 3, but only one character was changed. Why does this happen?
The reason is that Python treats these two strings as string types, and in the string type, under the default utf-8 encoding, a Chinese character is represented by three bytes.
The solution is to convert the string into unicode format, which will return the correct result 1.
# -*- coding:utf-8 -*- import Levenshtein texta = u'艾伦 图灵传' textb = u'艾伦•图灵传' print Levenshtein.distance(texta,textb)
Next, we will focus on the functions of several methods of taking care:
Levenshtein.distance(str1, str2)
Calculate edit distance (also called Levenshtein distance). It describes the minimum number of operations to convert one string into another. The operations include insertion, deletion, and replacement. Algorithm implementation: dynamic programming.
Levenshtein.hamming(str1, str2)
Calculate Hamming distance. It is required that str1 and str2 must be of the same length. It describes the number of different characters in the corresponding positions between two equal-length strings.
Levenshtein.ratio(str1, str2)
Calculate Levenstein ratio. Calculation formula r = (sum – ldist) / sum, where sum refers to the sum of the lengths of str1 and str2 strings, and ldist is the class edit distance. Note that this is the class edit distance. In the class edit distance, deletion and insertion are still +1, but replacement is +2.
Levenshtein.jaro(s1, s2)
Calculate jaro distance. Jaro Distance is said to be used to determine whether two names on health records are the same. It is also said to be used for census. Let’s first take a look at the definition of Jaro Distance.
The Jaro Distance of two given strings S1 and S2 is:
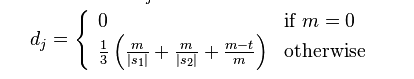
where m is the number of characters matched by s1 and s2, and t is the number of transpositions.
If the distance between two characters from S1 and S2 is no more than
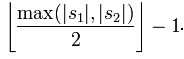
, we consider the two strings to be matching; and these matching characters determine the number of transpositions t, To put it simply, half of the number of matching characters in different orders is the number of transpositions t. For example, the characters of MARTHA and MARHTA both match, but among these matching characters, T and H need to be transposed to change MARTHA into MARHTA, then T and H are matching characters in different orders, t=2 /2=1.
The Jaro Distance of two strings is:
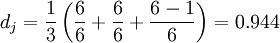
Levenshtein.jaro_winkler(s1, s2)
Calculate the Jaro–Winkler distance, and Jaro-Winkler gives higher scores to strings with the same starting part , he defined a prefix p, given two strings, if the prefix part has the same part of length ι, the Jaro-Winkler Distance is:
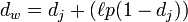
dj is the Jaro Distance of the two strings
"””’’ ’’’’’’’’’’’’’’’’’’’’’’’’’s’’’ '' '' - '' is the same length as the prefix. , the Jaro-Winkler Distance of MARTHA and MARHTA mentioned above is:
dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961
When analyzing Chinese, is it better to compare by words than by characters?
Summary
The above is the entire content of this article. I hope the content of this article can be helpful to everyone in learning or using python. If you have any questions, you can leave a message to communicate.