JavaScript의 데이터 구조 및 알고리즘(3): 연결된 목록

자바스크립트 개념의 큐와 스택은 특별한 선형 리스트 구조이면서도 비교적 단순한 배열 기반의 순차 저장 구조임을 알 수 있습니다. JavaScript 인터프리터는 배열에 대해 직접 최적화되었기 때문에 많은 프로그래밍 언어에서 배열의 길이가 고정되는 문제가 없을 것입니다. (배열이 가득 찬 후에는 추가 및 삭제를 포함하여 추가하는 것이 더 어렵습니다. 배열에서) 모든 요소의 위치가 변경되고 푸시, 팝, 시프트, unshift, 분할 메소드 등과 같은 JavaScript 배열이 실제로 직접 최적화됩니다...)

선형 테이블의 순차 저장 구조의 가장 큰 단점은 요소 중 하나의 배열을 변경하면 전체 컬렉션이 변경된다는 점입니다. 그 이유는 메모리 내 저장이 본질적으로 일관되고 간격이 없기 때문입니다. 하나의 요소를 삭제하면 자연스럽게 보완됩니다. 이 구조를 최적화한 후에는 체인 저장 구조가 등장했습니다. 사고방식을 바꾸려면 데이터의 배열에 전혀 신경 쓰지 않고 각 요소 내부에 다음 데이터의 위치만 기록하면 됩니다. 링크 모드에 저장된 선형 리스트를 줄여서 링크드 리스트라고 합니다. 링크 구조에서는 데이터 = (정보 주소)

체인 구조에서는 주소를 "체인"이라고 부를 수도 있습니다. 데이터 단위는 노드이므로 연결 목록은 노드의 모음이라고 할 수 있습니다. 각 노드에는 다음 노드를 가리키는 데이터 블록 참조가 있습니다

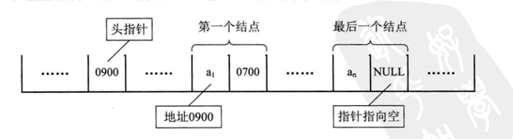
배열 요소는 위치 관계를 기반으로 논리적으로 참조되고, 연결 목록은 참조 포인터 관계를 저장하는 각 데이터 요소를 기반으로 참조됩니다.

이 구조의 장점은 매우 분명합니다. 데이터를 삽입할 때 배열에 대해 전혀 걱정할 필요가 없습니다. "체인"의 방향만 연결하면 됩니다.

이러한 연결 목록의 개념은 객체 간에 참조 관계가 있는 한 배열에만 국한되지 않습니다.

리드에는 일반적으로 단일 연결 목록, 정적 연결 목록, 순환 연결 목록, 이중 연결 목록이 포함됩니다

단일 연결 목록: 매우 간단한 하향 전송입니다. 각 노드는 다음 노드의 정보만 기록합니다. 무간도의 Tony Leung과 마찬가지로 잠복 요원은 중개자를 통해 온라인 및 오프라인과 통신합니다. 끊어지면 신원을 증명할 수 없어서 영화 마지막에 "나는 좋은 사람이에요. 누가 알겠어요?"라는 문장이 나옵니다.

정적 연결 리스트: 배열로 설명하는 연결 리스트입니다. 즉, 배열의 각 테이블은 데이터와 포인터를 포함하는 "섹션"입니다.

순환 연결 리스트: 단일 연결 리스트는 뒤로만 전달되기 때문에 끝에 도달하면 다시 헤드로 돌아가는 것이 매우 번거로우므로 tail 부분의 체인을 헤드에 연결하여 형태를 이룬다. 루프

이중 연결 목록: 단일 연결 목록에 대한 최적화로 각 섹션에서 누가 이전과 이후인지 알 수 있으므로 백 포인터 필드 외에 프런트 포인터 필드도 있어 검색 효율성이 향상되지만, 일부 디자인 문제 발생 일반적으로 복잡성은 공간과 시간을 교환하는 것입니다

결론적으로 연결 리스트는 선형 리스트의 순차 저장 구조에 대한 최적화 방법이지만, 자바스크립트 언어에서는 배열의 특수성(참조 위치 자동 업데이트)으로 인해 객체를 사용하여 구조를 저장할 수 있습니다

단일 연결 리스트

가장 간단한 연결리스트 관계를 구현합니다

function createLinkList() {
  var _this = {},
    prev = null;
  return {
    add: function(val) {
      //保存当前的引用
      prev = {
        data: val,
        next: prev || null
      }
    }
  }
}
var linksList = createLinkList(); 
linksList.add("arron1"); 
linksList.add("arron2"); 
linksList.add("arron3");
//node节的next链就是 -arron3-arron2-arron1

로그인 후 복사

<… . 이 구현에는 또 다른 가장 중요한 문제가 있습니다. 실행된 섹션 뒤에 데이터를 어떻게 동적으로 삽입합니까?

그래서 우리는 이 노드 체인의 데이터를 검색한 다음 해당 데이터를 찾고 현재 체인에 새 섹션을 삽입하고 위치 레코드를 다시 작성하는 순회 방법을 설계해야 합니다

//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
  return function(key){
    //循环找到执行的节，如果没有返回本身
    while (currNode.data != key) {
      currNode = currNode.next;
    }
    return currNode;        
  }
}(headNode);

로그인 후 복사

해당 섹션 정보를 찾을 때까지 원래의 헤드 headNode 섹션을 전달하여 다음 섹션을 검색하여 현재 섹션을 찾는 방법입니다

카레 방식을 이용하여 구현한 것입니다

그러면 섹션 삽입 시 연결리스트 주소의 변환 관계는 다음과 같습니다

a-b-c-d의 연결 리스트에서 c(c.next->d) 뒤에 f

를 삽입하려는 경우

a-b-c-f-d, 그 다음 c,next->f, f.next-d

삽입 방법을 통해 섹션 추가

首先分离出createNode节的构建，在初始化的时候先创建一个头部节对象用来做节开头的初始化对象

在insert增加节方法中，通过对headNode链的一个查找，找到对应的节，把新的节给加后之后，最后就是修改一下链的关系

如何从链表中删除一个节点？

由于链表的特殊性，我们a->b->c->d ，如果要删除c那么就必须修改b.next->c为 b.next->d，所以找到前一个节修改其链表next地址，这个有点像dom操作中removeChild找到其父节点调用移除子节点

同样的我们也在remove方法的设计中，需要设计一个遍历往上回溯一个父节点即可

//找到前一个节
var findPrevious = function(currNode) {
  return function(key){
    while (!(currNode.next == null) &&
      (currNode.next.data != key)) {
      currNode = currNode.next;
    }
    return currNode;      
  }
}(headNode);

//插入方法
this.remove = function(key) {
  var prevNode = findPrevious(key);
  if (!(prevNode.next == null)) {
    //修改链表关系
    prevNode.next = prevNode.next.next;
  }
};

로그인 후 복사

测试代码：

<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">
 //////////
 //创建链表 //
 //////////
 function createLinkList() {

 //创建节
 function createNode(data) {
  this.data = data;
  this.next = null;
 }

 //初始化头部节
 //从headNode开始形成一条链条
 //通过next衔接
 var headNode = new createNode("head");

 //在链表中找到对应的节
 var findNode = function createFindNode(currNode) {
  return function(key) {
  //循环找到执行的节，如果没有返回本身
  while (currNode.data != key) {
   currNode = currNode.next;
  }
  return currNode;
  }
 }(headNode);

 //找到前一个节
 var findPrevious = function(currNode) {
  return function(key) {
  while (!(currNode.next == null) &&
   (currNode.next.data != key)) {
   currNode = currNode.next;
  }
  return currNode;
  }
 }(headNode);


 //插入一个新节
 this.insert = function(data, key) {
  //创建一个新节
  var newNode = new createNode(data);
  //在链条中找到对应的数据节
  //然后把新加入的挂进去
  var current = findNode(key);
  //插入新的接，更改引用关系
  //1:a-b-c-d
  //2:a-b-n-c-d
  newNode.next = current.next;
  current.next = newNode;
 };

 //插入方法
 this.remove = function(key) {
  var prevNode = findPrevious(key);
  if (!(prevNode.next == null)) {
  //修改链表关系
  prevNode.next = prevNode.next.next;
  }
 };


 this.display = function(fn) {
  var currNode = headNode;
  while (!(currNode.next == null)) {
  currNode = currNode.next;
  fn(currNode.data)
  }
 };

 }


 var cities = new createLinkList();

 function create() {
 var text = '';
 cities.display(function(data) {
  text += '-' + data;
 });
 var div = document.createElement('div')
 div.innerHTML = text;
 document.getElementById("listshow").appendChild(div)
 }

 document.getElementById("test1").onclick = function() {
 cities.insert("Conway", "head");
 cities.insert("Russellville", "Conway");
 cities.insert("Carlisle", "Russellville");
 cities.insert("Alma", "Carlisle");
 create();
 }

 document.getElementById("test2").onclick = function() {
 cities.remove("Russellville");
 create()
 }

</script>

로그인 후 복사

双链表

原理跟单链表是一样的，无非就是给每一个节增加一个前链表的指针

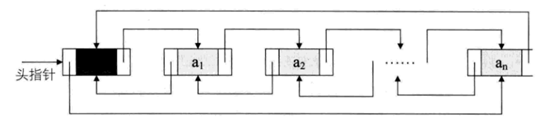
增加节

//插入一个新节
this.insert = function(data, key) {
  //创建一个新节
  var newNode = new createNode(data);
  //在链条中找到对应的数据节
  //然后把新加入的挂进去
  var current = findNode(headNode,key);
  //插入新的接，更改引用关系
  newNode.next   = current.next;
  newNode.previous = current
  current.next   = newNode;
};

로그인 후 복사

删除节

this.remove = function(key) {
  var currNode = findNode(headNode,key);
  if (!(currNode.next == null)) {
    currNode.previous.next = currNode.next;
    currNode.next.previous = currNode.previous;
    currNode.next     = null;
    currNode.previous   = null;
  }
};

로그인 후 복사

在删除操作中有一个明显的优化：不需要找到父节了，因为双链表的双向引用所以效率比单链要高

测试代码：

<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">

 //////////
 //创建链表 //
 //////////
 function createLinkList() {

 //创建节
 function createNode(data) {
  this.data = data;
  this.next = null;
  this.previous = null
 }

   //初始化头部节
 //从headNode开始形成一条链条
 //通过next衔接
 var headNode = new createNode("head");

 //在链表中找到对应的数据
 var findNode = function(currNode, key) {
  //循环找到执行的节，如果没有返回本身
  while (currNode.data != key) {
  currNode = currNode.next;
  }
  return currNode;
 }

 //插入一个新节
 this.insert = function(data, key) {
  //创建一个新节
  var newNode = new createNode(data);
  //在链条中找到对应的数据节
  //然后把新加入的挂进去
  var current = findNode(headNode,key);
  //插入新的接，更改引用关系
  newNode.next   = current.next;
  newNode.previous = current
  current.next   = newNode;
 };

 this.remove = function(key) {
  var currNode = findNode(headNode,key);
  if (!(currNode.next == null)) {
  currNode.previous.next = currNode.next;
  currNode.next.previous = currNode.previous;
  currNode.next     = null;
  currNode.previous   = null;
  }
 };

 this.display = function(fn) {
  var currNode = headNode;
  while (!(currNode.next == null)) {
  currNode = currNode.next;
  fn(currNode.data)
  }
 };

 }


 var cities = new createLinkList();

 function create() {
 var text = '';
 cities.display(function(data) {
  text += '-' + data;
 });
 var div = document.createElement('div')
 div.innerHTML = text;
 document.getElementById("listshow").appendChild(div)
 }

 document.getElementById("test1").onclick = function() {
 cities.insert("Conway", "head");
 cities.insert("Russellville", "Conway");
 cities.insert("Carlisle", "Russellville");
 cities.insert("Alma", "Carlisle");
 create();
 }

 document.getElementById("test2").onclick = function() {
 cities.remove("Russellville");
 create()
 }


</script>

로그인 후 복사

git代码下载：https://github.com/JsAaron/data_structure.git

JavaScript의 데이터 구조 및 알고리즘(3): 연결된 목록_javascript 기술