k-최근접 이웃 알고리즘은 분류 및 인식을 위한 인스턴스 기반 또는 메모리 기반 기계 학습 알고리즘입니다. 주어진 쿼리 포인트의 가장 가까운 이웃 데이터를 찾아 분류하는 것을 원칙으로 합니다. 알고리즘은 저장된 훈련 데이터에 크게 의존하기 때문에 비모수적 학습 방법으로 볼 수 있습니다.
k 최근접 이웃 알고리즘은 분류 또는 회귀 문제를 처리하는 데 적합합니다. 분류 문제의 경우 이산 값으로 작동하는 반면 회귀 문제의 경우 연속 값으로 작동합니다. 분류하기 전에 거리를 정의해야 하며 일반적인 거리 측정에 대한 선택 사항이 많이 있습니다.
이것은 실제 값 벡터에 작동하는 일반적으로 사용되는 거리 측정입니다. 이 수식은 쿼리 점과 다른 점 사이의 직선 거리를 측정합니다.
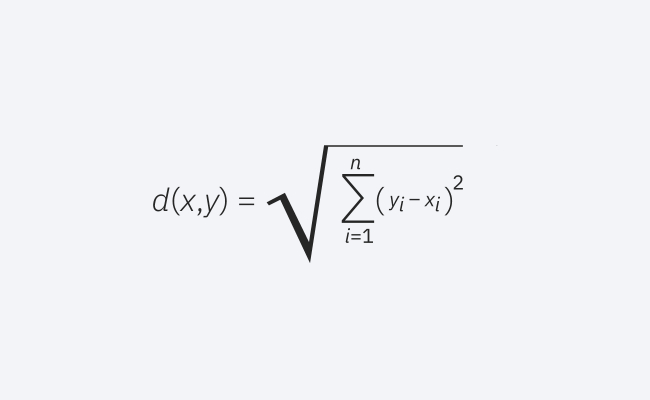
유클리드 거리 공식
이것은 두 점 사이의 절대값을 측정하는 인기 있는 거리 측정 방법이기도 합니다.

Manhattan 거리 공식
이 거리 측정은 유클리드 및 맨해튼 거리 측정을 일반화한 형태입니다.

Minkowski 거리 공식
이 기술은 벡터가 일치하지 않는 지점을 식별하기 위해 부울 또는 문자열 벡터와 함께 자주 사용됩니다. 따라서 중첩 측정이라고도 합니다.

해밍 거리 공식
어떤 데이터 포인트가 주어진 쿼리 포인트에 가장 가까운지 결정하려면 쿼리 포인트와 다른 데이터 포인트 사이의 거리를 계산해야 합니다. 이러한 거리 측정값은 쿼리 지점을 여러 영역으로 나누는 결정 경계를 형성하는 데 도움이 됩니다.
위 내용은 K 최근접 이웃 알고리즘에서 일반적으로 사용되는 거리 측정 방법 적용의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!