matlab을 사용하여 미분방정식 5261 수치해 4102 초기값 문제와 분석해를 풀면 다음과 같이 처리할 수 있습니다.
1. 수치해석
미분방정식의 초기값 문제에 대한 수치해는 ode 함수를 사용하여 풀 수 있습니다.
먼저 미분방정식의 기능을 맞춤설정하세요. 즉
dy = 3/x*y+x^3*(exp(x)+cos(x))-2*x;
둘째, 초기 조건을 결정합니다. 즉
y0=[(exp(pi)+2/pi)*pi^3];
셋째, ode45 함수를 사용하여 수치해 [x, y]를 구합니다
2. 분석 솔루션
미분 방정식의 초기값 문제에 대한 분석적 해는 dsolve 함수를 사용하여 풀 수 있습니다.
먼저 y(x)에 대한 변수를 선언합니다. 즉,
심즈 y(x)
두 번째, y(x)의 첫 번째 도함수는
Dy=차이(y,1)
셋째, dsolve 함수를 사용하여 분석 해 y(x)의 표현식을 찾습니다.
y=dsolve(Dy==3/x*y+x^3*(exp(x)+cos(x))-2*x,y(pi)==(exp(pi)+2/pi) *파이^3)
3. 수치해와 해석해 곡선 그리기
먼저, 플롯 기능을 사용하여 수치해의 곡선을 그립니다
플롯(x.y)
두 번째, [π, 2π] 구간에서 일련의 x 값에 대해 y와 동일한 y 값을 계산합니다
셋째, 플롯 기능을 사용하여 분석 솔루션의 곡선을 그립니다
코드를 실행하면 다음과 같은 결과를 얻을 수 있습니다.
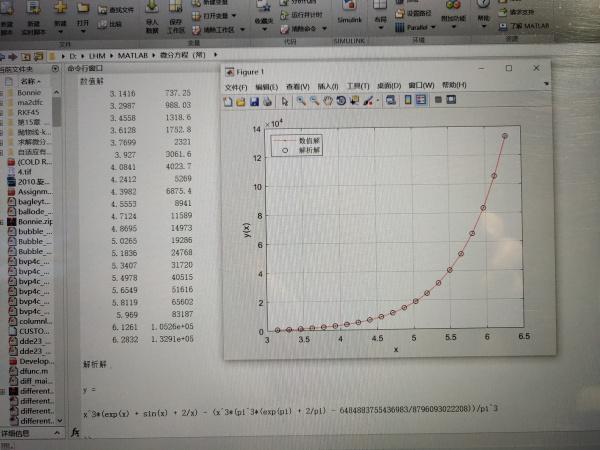
%%%%%%%%%%%%%%%%%%% 소스 프로그램
i=0;equ=0;sum=0;
data=input('숫자를 입력하세요: ');
동안(데이터~=0)
합계=합계+데이터;
key=input('계속하세요: ');
데이터=키;
i=i+1;
끝
equ=sum/i;
equ,sum
%%%%%%%%%%%%%%%%%%%%%%%%%
실행 결과:
숫자 1을 입력해주세요
계속하세요: 2
계속하세요: 3
계속하세요: 4
계속하세요: 5
계속하세요: 0
equ=
3
합 =
15
위 내용은 간격 내 미분방정식의 초기값 문제에 대한 수치해석적 해법의 Matlab 구현 방법과 그래픽 표시의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!