로컬 최소값을 찾기 위해 Python에서 경사하강법 알고리즘을 구현하는 방법은 무엇입니까?

경사하강법은 기계 학습에서 중요한 최적화 방법으로, 모델의 손실 함수를 최소화하는 데 사용됩니다. 일반인의 관점에서는 손실 함수를 최소화하는 이상적인 값 범위를 찾을 때까지 모델의 매개변수를 반복적으로 변경해야 합니다. 이 방법은 손실 함수의 음의 기울기 방향으로, 더 구체적으로 가장 가파른 하강 경로를 따라 작은 단계를 밟는 방식으로 작동합니다. 학습률은 알고리즘 속도와 정확도 간의 균형을 조절하는 하이퍼파라미터로, 단계 크기에 영향을 줍니다. 선형 회귀, 로지스틱 회귀, 신경망 등을 비롯한 많은 기계 학습 방법에서는 경사하강법을 사용합니다. 주요 응용 프로그램은 모델 교육으로, 목표 변수의 예상 값과 실제 값 간의 차이를 최소화하는 것이 목표입니다. 이 기사에서는 로컬 최소값을 찾기 위해 Python에서 경사하강법을 구현하는 방법을 살펴보겠습니다.

이제 Python에서 경사하강법을 구현할 차례입니다. 구현 방법에 대한 기본 설명은 다음과 같습니다. -

• 먼저 필요한 라이브러리를 가져옵니다.

• 함수와 파생어를 정의하세요.

• 다음으로 경사 하강 기능을 적용해 보겠습니다.

• 함수를 적용한 후 매개변수를 설정하여 지역 최소값을 찾습니다.

• 마지막으로 출력을 플롯합니다.

Python에서 경사하강법 구현

라이브러리 가져오기

그런 다음 함수 f(x)와 그 도함수 f'(x)를 정의합니다. -

F(x)는 축소되어야 하는 함수이고 df는 그 도함수(x)입니다. 경사하강법은 도함수를 사용하여 도중에 함수의 기울기를 밝혀 최소값을 향해 스스로를 안내합니다.

그런 다음 경사하강법 함수를 정의합니다.

x의 시작 값, 학습률 및 필요한 반복 횟수가 경사하강법 함수로 전송됩니다. 각 반복 후에 x 값을 저장하기 위해 x를 원래 값으로 초기화하고 빈 목록을 생성합니다. 그런 다음 이 메서드는 x = x - 학습 속도 * 기울기 방정식에 따라 각 반복에서 x를 변경하면서 제공된 반복 횟수에 대해 경사하강법을 수행합니다. 이 함수는 각 반복에 대한 x 값 목록과 x의 최종 값을 생성합니다.

이제 경사하강법 함수를 사용하여 f(x)의 국소 최소값을 찾을 수 있습니다. -

예

출력

이 그림에서 x는 초기에 0으로 설정되고 학습률은 0.1이며 50번의 반복이 실행됩니다. 마지막으로 x=2에서 로컬 최소값에 가까워야 하는 x 값을 게시합니다.

함수 f(x)와 각 반복에 대한 x 값을 플로팅하면 실제 경사하강법 과정을 볼 수 있습니다. -

예제

import numpy as np
import matplotlib.pyplot as plt

출력

결론

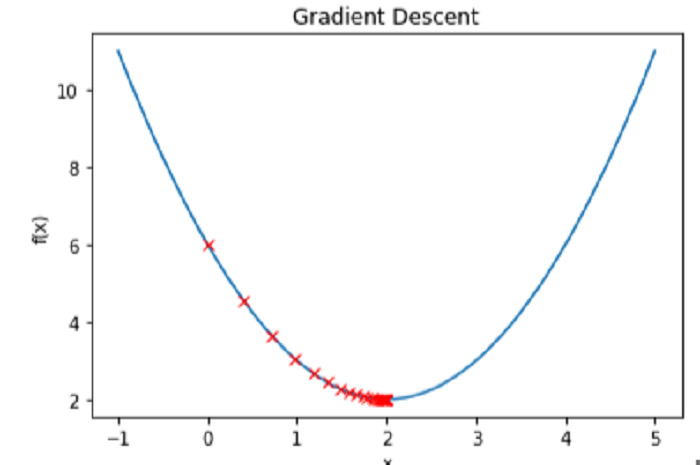
요약하자면, 함수의 국소 최소값을 찾기 위해 Python은 경사하강법이라는 효율적인 최적화 프로세스를 활용합니다. 경사하강법은 각 단계에서 함수의 도함수를 계산하여 가장 낮은 값에 도달할 때까지 가장 가파른 하강 방향으로 입력 값을 반복적으로 업데이트하는 방식으로 작동합니다. Python에서 경사하강법을 구현하려면 최적화할 함수와 그 파생 함수를 지정하고, 입력 값을 초기화하고, 알고리즘의 학습 속도와 반복 횟수를 결정해야 합니다. 최적화가 완료된 후, 최소 단계까지 추적하고 해당 목표에 어떻게 도달하는지 확인하여 방법을 평가할 수 있습니다. 경사 하강법은 Python이 대규모 데이터 세트와 복잡한 기능을 처리할 수 있기 때문에 기계 학습 및 최적화 애플리케이션에 유용한 기술입니다.

위 내용은 로컬 최소값을 찾기 위해 Python에서 경사하강법 알고리즘을 구현하는 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!