활성화, 가중치 및 기울기를 4비트로 양자화하면 신경망 훈련 속도가 빨라질 것으로 예상됩니다.
그러나 기존 4자리 훈련 방법에는 최신 하드웨어에서 지원되지 않는 맞춤 숫자 형식이 필요합니다.
최근 Tsinghua Zhu Jun 팀은 INT4 알고리즘을 사용하여 모든 행렬 곱셈을 구현하는 Transformer 훈련 방법을 제안했습니다.
매우 낮은 INT4 정확도로 훈련하는 것은 매우 어렵습니다. 이 목표를 달성하기 위해 연구자들은 Transformer의 특정 활성화 및 기울기 구조를 주의 깊게 분석하고 이를 위한 전용 양자화기를 제안했습니다.
연구원들은 순방향 전파를 위해 이상값의 문제를 식별하고 이상값을 억제하기 위해 Hadamard 양자화기를 제안했습니다.
역전파의 경우 비트 분할을 제안하여 기울기의 구조적 희소성을 활용하고 분수 샘플링 기술을 활용하여 기울기를 정확하게 정량화합니다.
이 새로운 알고리즘은 자연어 이해, 기계 번역, 이미지 분류를 포함한 광범위한 작업에서 경쟁력 있는 정확도를 달성합니다.
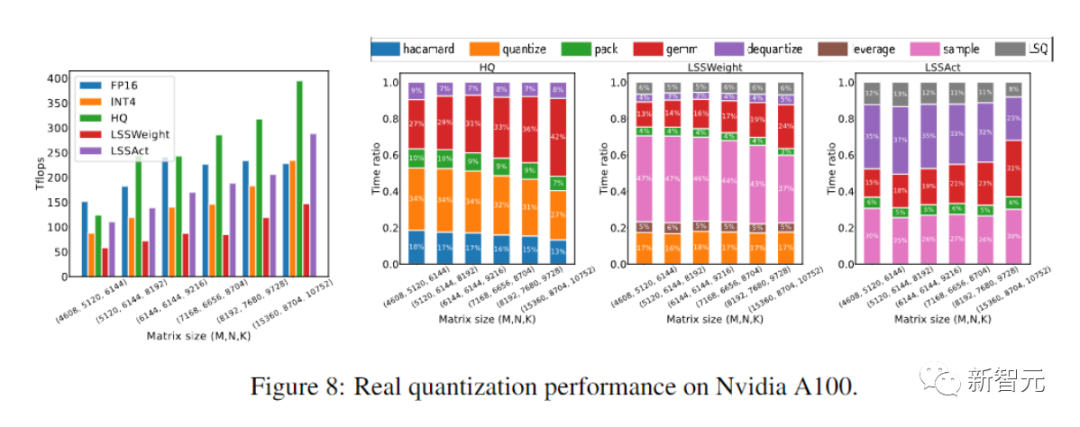
프로토타입 선형 연산자는 FP16의 유사한 연산자보다 2.2배 빠르며 훈련 속도는 35.1% 증가했습니다.
Pictures
문서 주소: https://arxiv.org/abs/2306.11987
코드 주소: https://github.com/xijiu9/Train_Transformers_with_INT4
신경망 훈련은 계산량이 매우 많습니다. 정밀도가 낮은 산술(완전 양자화 훈련/FQT)을 사용한 훈련은 계산 및 메모리 효율성을 향상시킬 것으로 예상됩니다.
FQT 방법은 원래 완전 정밀도 계산 그래프에 일부 양자화기와 역양자화기를 추가하고 더 비싼 부동 소수점 연산을 덜 비싼 저정밀도 부동 소수점 연산으로 대체합니다.
FQT 연구는 수렴 속도나 정확도를 너무 많이 희생하지 않고 훈련 수치 정확도를 줄이는 것을 목표로 합니다.
필요한 수치 정밀도가 FP16에서 FP8, INT32+INT8 및 INT8+INT5로 감소했습니다.
FP8 교육은 Transformer 엔진이 탑재된 Nvidia H100 GPU에서 구현되어 대규모 Transformer 교육을 가속화합니다. 최근 훈련 수치 정확도가 4자리로 떨어졌습니다.
그러나 이러한 4비트 훈련 방법은 최신 하드웨어에서 지원하지 않는 사용자 정의 숫자 형식이 필요하기 때문에 가속에 직접 사용할 수 없습니다.
우선, 순방향 전파에서 미분 불가능한 양자화기는 손실 상황을 울퉁불퉁하게 만들고, 기울기 기반 최적화기는 쉽게 로컬 최적해에 빠질 수 있습니다.
두 번째로 기울기는 낮은 정밀도로만 근사화됩니다. 이러한 부정확한 기울기로 인해 훈련 과정이 느려지고 심지어 훈련이 불안정해지거나 분산될 수도 있습니다.
이 연구에서 연구원들은 Transformer를 위한 새로운 INT4 훈련 알고리즘을 제안했습니다.
Pictures
Transformer 학습을 위한 모든 고비용 선형 연산은 행렬 곱셈(MM) 형식으로 작성할 수 있습니다.
이 MM 형식을 사용하면 Transformer의 특정 활성화, 가중치 및 그래디언트 구조를 활용하여 FP32 행렬 곱셈에 더 잘 근접할 수 있는 보다 유연한 양자화기를 설계할 수 있습니다.
이 양자화기는 RandNLA(Random Numerical Linear Algebra) 분야의 발전을 완벽하게 활용합니다.
순방향 전파의 경우 연구원들은 활성화의 이상값이 정확도 감소의 주요 원인임을 발견했습니다.
이상값을 억제하기 위해 그들은 활성화 행렬의 변환된 버전을 양자화하는 Hadamard 양자화기를 제안했습니다. 이 변환은 이상값에 포함된 정보를 행렬의 인접 항목으로 전파하여 이상값의 수치 범위를 좁히는 블록 대각 Hadamard 행렬입니다.
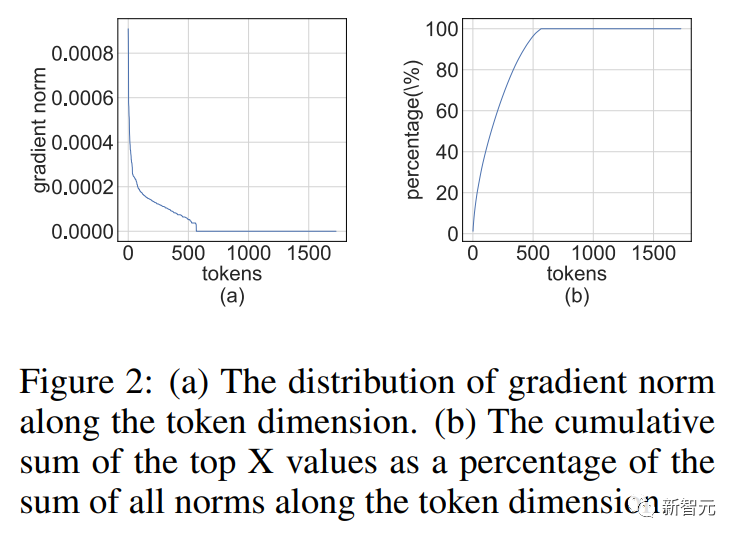
역전파의 경우 활성화 기울기의 구조적 희소성을 활용합니다. 연구원들은 일부 토큰의 기울기가 매우 크다는 것을 발견했습니다. 동시에 대부분의 다른 토큰의 기울기는 매우 균일하며, 큰 기울기의 양자화된 잔차보다 훨씬 더 균일합니다.
Pictures
따라서 모든 기울기를 계산하는 대신 더 큰 기울기 잔차를 계산하는 데 필요한 계산 리소스를 절약하는 것이 좋습니다.
이 희소성을 활용하기 위해 연구원들은 각 토큰의 기울기를 상위 4비트와 하위 4비트로 나누는 비트 파티셔닝을 제안했습니다.
그런 다음 RandNLA의 중요한 샘플링 기법인 레버리지 점수 샘플링을 통해 가장 유익한 그래디언트를 선택합니다.
Pictures
연구원들은 순방향 전파와 역방향 전파의 양자화 기술을 결합하여 INT4MM을 사용하여 Transformer에서 모든 선형 연산을 수행하는 알고리즘을 제안하고 자연어를 포함한 다양한 작업에 대해 Transformer를 훈련시키는 알고리즘을 평가했습니다. 이해, 질문 답변, 기계 번역 및 이미지 분류.
해당 알고리즘은 기존 4비트 학습 알고리즘에 비해 경쟁력이 있거나 더 높은 정확도를 달성합니다.
또한 이 알고리즘은 FP4 또는 로그 형식과 같은 사용자 정의 숫자 형식이 필요하지 않기 때문에 GPU와 같은 최신 하드웨어와 호환됩니다.
이 프로토타입 양자화 + INT4 MM 연산자 구현은 FP16MM 기준보다 2.2배 빠르고 훈련 속도를 35.1% 증가시킵니다.
완전 양자화 훈련(FQT) 방법은 활성화, 가중치 및 기울기를 낮은 정밀도로 양자화하여 훈련 속도를 높입니다. 따라서 훈련 중 선형 및 비선형 연산자는 낮은 사용을 사용하여 구현됩니다. -정밀한 산술.
FQT 연구에서는 완전 정밀도 텐서에 더 잘 근접할 수 있는 새로운 수치 형식과 양자화 알고리즘을 설계했습니다.
현재 연구 분야는 4자리 FQT입니다. FQT는 기울기의 수치 범위가 크고 양자화된 네트워크를 처음부터 훈련시키는 최적화 문제로 인해 어렵습니다.
이러한 문제로 인해 기존 4비트 FQT 알고리즘은 여전히 일부 작업에서 1~2.5%의 정확도 손실을 겪고 있으며 최신 하드웨어를 지원할 수 없습니다.
Pictures
전문가를 혼합하면 훈련 예산을 늘리지 않고도 모델 용량이 늘어납니다.
구조적 드롭아웃은 계산적으로 효율적인 방법을 활용하여 모델을 정규화합니다. 효율적인 주의는 주의 계산의 2차 시간 복잡도를 줄입니다.
분산 교육 시스템은 더 많은 컴퓨팅 리소스를 활용하여 교육 시간을 단축합니다.
수치 정확도를 낮추려는 연구자들의 작업은 이러한 방향과 직교합니다.
Pictures
순방향 전파
신경망 훈련은 순방향 및 역방향 전파를 통해 확률적 경사를 계산하는 반복 최적화 프로세스입니다.
연구팀은 순방향 및 역방향 전파를 가속화하기 위해 4비트 정수(INT4) 알고리즘을 사용합니다.
순방향 전파는 선형 및 비선형(GeLU, 정규화, 소프트맥스 등) 연산자의 조합으로 구현할 수 있습니다.
교육 과정에서 INT4 산술을 사용하여 모든 선형 연산자를 가속화하고 계산 비용이 덜 드는 모든 비선형 연산자를 16비트 부동 소수점(FP16) 형식으로 유지합니다.
Transformer의 모든 선형 연산은 행렬 곱셈(MM) 형식으로 작성할 수 있습니다.
표현의 용이성을 위해 이 기사에서는 다음과 같은 단순 행렬 곱셈의 가속도를 고려합니다.
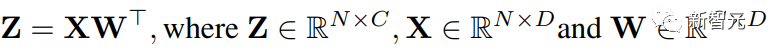Picture
이런 종류의 MM의 주요 사용 사례는 완전 연결 레이어입니다.
입력 형태가 (배치 크기 S, 시퀀스 길이 T, 차원 D)인 변환기를 생각해 보세요.
완전히 연결된 레이어는 위의 공식으로 표현될 수 있습니다. 여기서 X는 N = STtoken의 활성화이고 W는 가중치 행렬입니다.
주의 레이어에는 BMMS(배치 행렬 곱셈)가 필요할 수 있습니다.
우리가 제안한 기술은 BMMS에 적용될 수 있습니다.
훈련 속도를 높이려면 정수 연산을 사용하여 순방향 전파를 계산해야 합니다.
연구원들은 이러한 목적으로 LSQ(Learning Step Quantizer)를 활용했습니다.
LSQ는 양자화 규모가 입력 방법에 의존하지 않으므로 각 반복에서 양자화 규모를 동적으로 계산해야 하는 동적 방법보다 비용이 저렴합니다.
이상값 활성화
단순히 4비트 활성화/가중치를 사용하여 FQT에 LSQ를 적용하면 이상값이 활성화되므로 정확도가 떨어집니다.
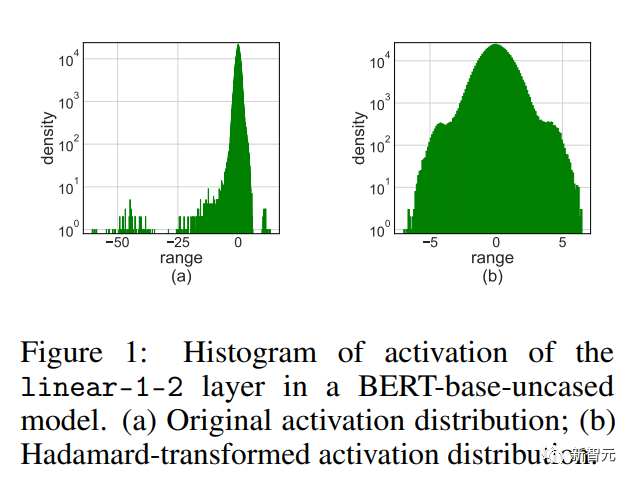Picture
위 그림과 같이 활성화에는 다른 항목보다 크기가 훨씬 큰 일부 특이 항목이 있습니다.
안타깝게도 Transformer는 이러한 이상값에 정보를 저장하는 경향이 있으며 이러한 잘림은 정확성을 심각하게 손상시킬 수 있습니다.
특이점 문제는 훈련 작업이 일부 새로운 다운스트림 작업에 대해 사전 훈련된 모델을 미세 조정하는 것일 때 특히 분명합니다.
사전 훈련된 모델에는 무작위 초기화보다 더 많은 이상값이 포함되어 있기 때문입니다.
이상값 문제를 해결하기 위해 Hadamard Quantization(HQ)을 제안합니다.
주요 아이디어는 더 적은 수의 이상값을 사용하여 선형 공간에서 다른 행렬을 양자화하는 것입니다.
활성화 행렬의 이상값은 기능별 구조를 형성합니다.
일반적으로 몇 가지 차원에 집중되어 있습니다. 즉, X의 소수 열만 다른 열보다 훨씬 큽니다.
Hardamand 변환은 이상값을 다른 항목으로 확산시키는 선형 변환입니다.
역전파
이제 선형 레이어의 역전파 속도를 높이기 위해 INT4 작업을 사용하는 것을 고려합니다.
이 섹션에서는 활성화 기울기/중량 기울기 계산에 대해 논의합니다.
우리는 훈련 중에 그래디언트 행렬이 매우 희박해지는 경향이 있음을 발견했습니다.
희소성은 다음과 같은 구조를 갖습니다.
의 몇 행(예: 토큰)에는 큰 항목이 있고 대부분의 다른 행은 모두 0인 벡터에 가깝습니다.
Pictures
이 구조적 희소성은 현대 신경망의 심각한 과잉 매개변수화로 인해 발생합니다.
네트워크는 거의 전체 훈련 프로세스에 대해 초매개변수화 방식으로 실행되며 몇 가지 어려운 예를 제외하고 대부분의 훈련 데이터에 잘 적응합니다.
따라서 잘 맞는 데이터 포인트의 경우 (활성화) 기울기는 0에 가까워집니다.
연구원들은 예를 들어 사전 훈련 작업의 경우 몇 번의 훈련 에포크 후에 구조적 희소성이 빠르게 나타난다는 것을 발견했습니다.
미세 조정 작업의 경우 훈련 과정 전체에서 기울기가 항상 희박합니다.
구조적 희소성을 사용하여 역전파 중에 MM을 정확하게 계산하기 위해 그래디언트 양자화기를 설계하는 방법은 무엇입니까?
고급 아이디어는 다음과 같습니다. 많은 그라디언트 행이 너무 작아서 매개변수 그라디언트에 거의 영향을 미치지 않지만 많은 계산을 낭비합니다.
반면에 대형 은행은 INT4로 정확하게 표현할 수 없습니다.
작은 행 몇 개를 삭제하고 저장된 컴퓨팅 성능을 사용하여 큰 행을 더 정확하게 표현합니다.
실험
연구원들은 언어 모델, 기계 번역 및 이미지 분류를 포함한 다양한 작업에 대한 INT4 교육 알고리즘의 미세 조정을 평가합니다.
연구원들은 CUDA와 커틀라스를 사용하여 제안된 HQ-MM 및 LSS-MM 알고리즘을 구현했습니다.
연구원들은 모든 부동 소수점 선형 연산자를 INT4 구현으로 대체했지만 단순히 LSQ를 사용하여 레이어를 삽입하고 마지막 분류기 레이어의 정확도를 유지하지는 않았습니다.
마지막으로 연구원들은 평가된 모든 모델에 대해 기본 아키텍처, 최적화 프로그램, 스케줄러 및 하이퍼 매개변수를 채택했습니다.
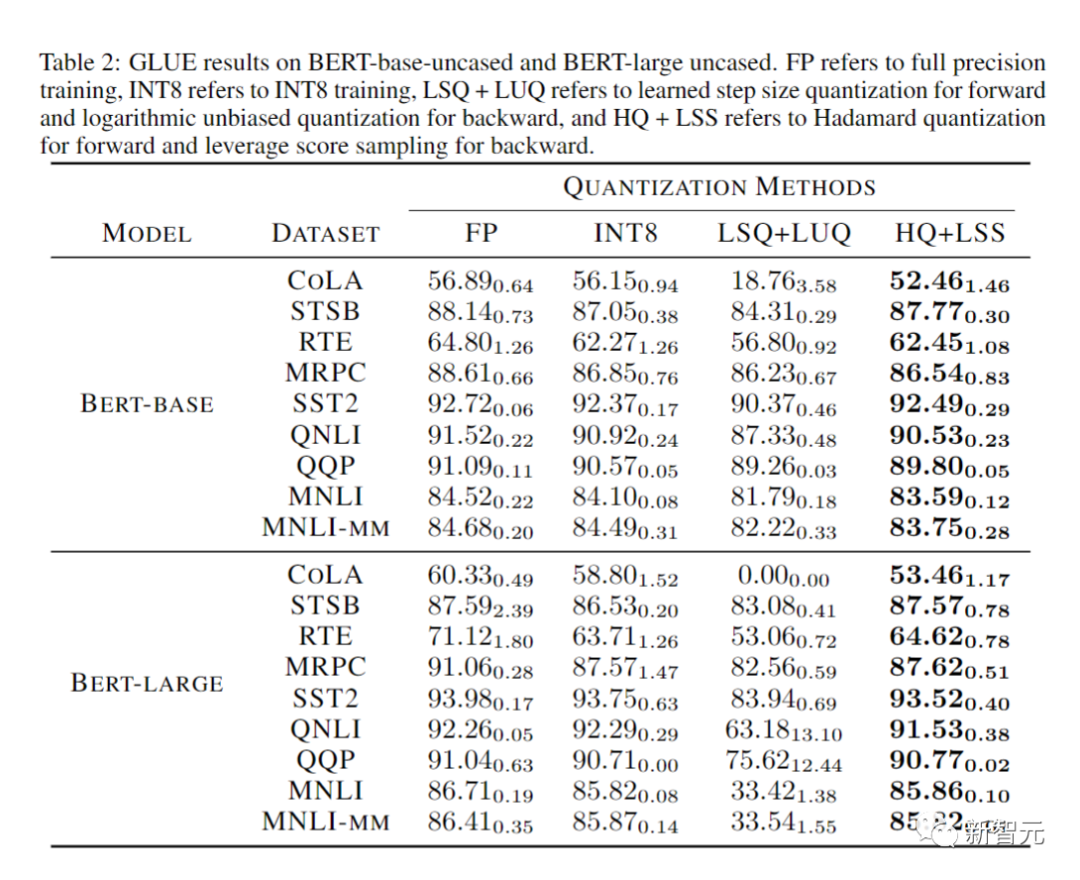
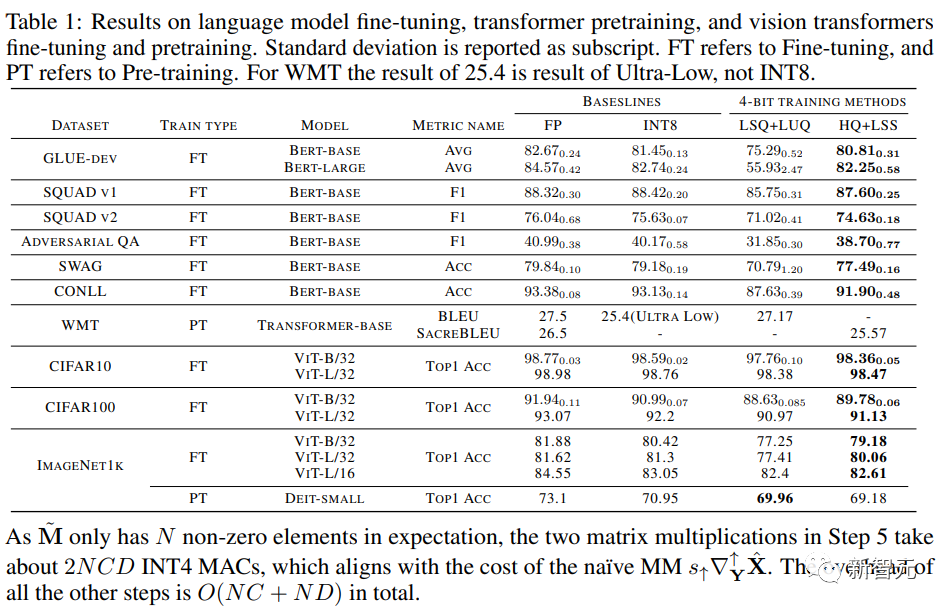
연구원들은 아래 표에서 다양한 작업에 대한 수렴 모델의 정확도를 비교했습니다.
Pictures
비교 방법에는 완전 정밀 훈련(FP), INT8 훈련(INT8), FP4 훈련("초저"), 활성화 및 가중치를 위해 LSQ 사용(LSQ+LUQ)이 포함됩니다. 4비트 로그 양자화 및 순방향 전파에 HQ를 사용하고 역전파에 LSS(HQ+LSS)를 사용하는 알고리즘입니다.
"Ultra Low"는 공개 구현이 없으므로 기계 번역 작업에 대한 원본 논문에만 성능을 나열합니다.
대규모 기계 번역 작업과 대규모 시각적 Transformer 작업을 제외하고 각 실행을 세 번 반복하고 표의 아래 첨자로 표준 편차를 보고합니다.
연구원들은 어떤 유형의 지식 증류나 데이터 증대도 수행하지 않았습니다.
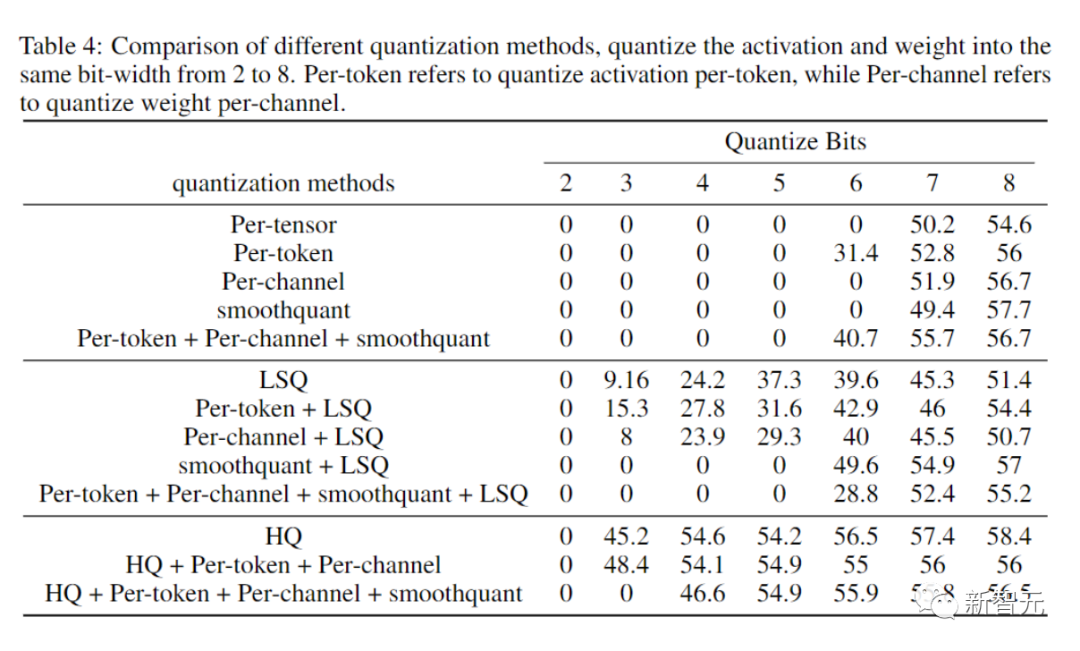
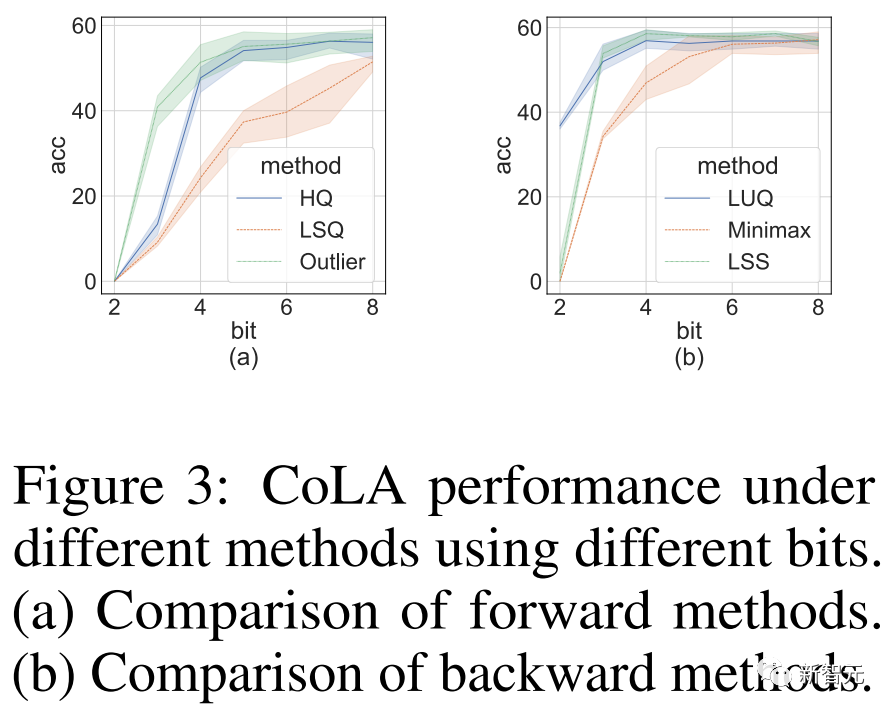
연구원들이 실시한 절제 실험의 목적은 전방향 및 역방향 방법의 효과를 입증하는 것이었습니다.
다양한 양자화기의 순방향 전파 효과를 연구하기 위해 FP16에는 역방향 전파를 그대로 둡니다.
결과는 아래 사진과 같습니다.
Pictures
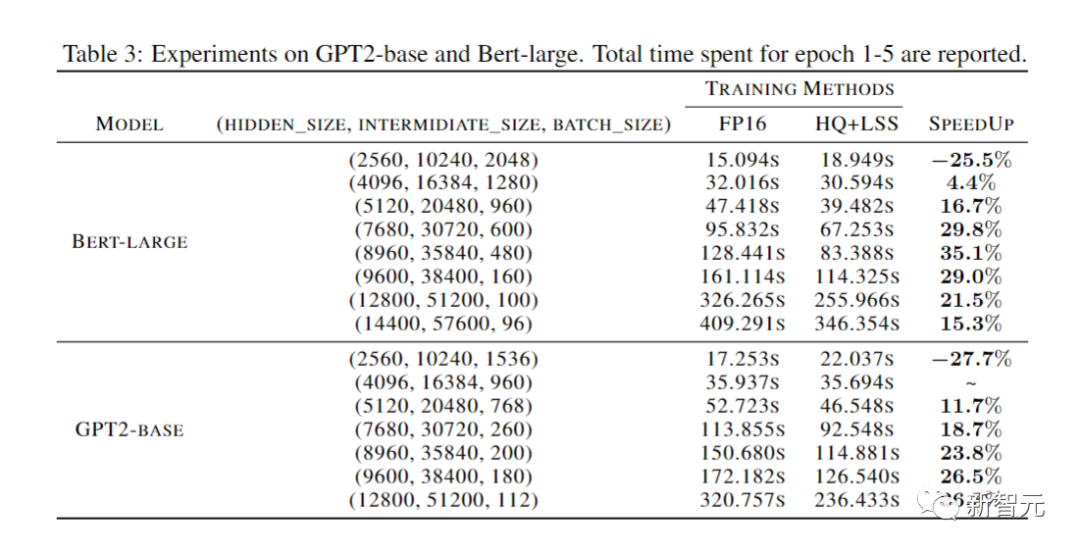
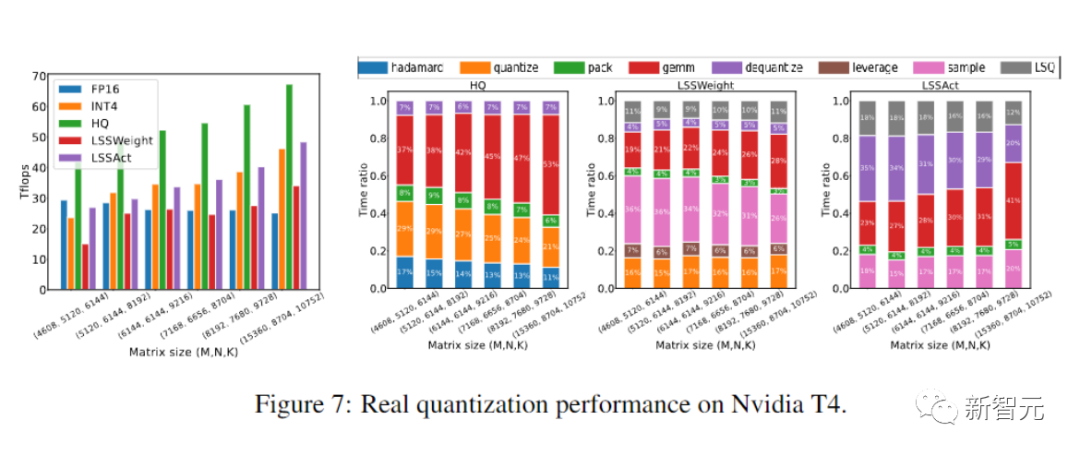
마지막으로 연구원들은 프로토타입 구현을 평가하여 신경망 훈련을 가속화하는 접근 방식의 잠재력을 입증했습니다.
그리고 구현이 아직 완전히 최적화되지 않았습니다.
연구원들은 또한 선형 연산자를 비선형성 및 정규화와 융합하지 않았습니다.
따라서 결과는 INT4 훈련 알고리즘의 잠재력을 완전히 반영하지 않습니다.
완전히 최적화된 구현에는 광범위한 엔지니어링이 필요하며 이는 이 문서의 범위를 벗어납니다.
연구원들은 Transformer INT4를 위한 하드웨어 친화적인 훈련 방법을 제안했습니다.
연구원들은 Transformer에서 MM의 속성을 분석하여 정확도를 유지하면서 활성화 및 기울기를 정량화하는 HQ 및 LSS 방법을 제안했습니다.
몇 가지 중요한 작업에서 우리의 방법은 기존 INT4 방법과 동일하거나 더 나은 성능을 발휘합니다.
연구원의 작업은 Transformers 외에 MLP-Mixer, 그래프 신경망 및 순환 신경망 네트워크와 같은 다른 MM 아키텍처로 확장될 수 있습니다.
이것이 그들의 향후 연구 방향입니다.
더 넓은 영향: 연구원의 알고리즘은 효율성을 높이고 신경망 훈련의 에너지 소비를 줄여 딥 러닝으로 인한 탄소 배출을 줄이는 데 도움이 될 수 있습니다.
그러나 효율적인 훈련 알고리즘은 인간의 보안 위험을 초래하는 대규모 언어 모델 및 악성 AI 애플리케이션의 개발을 촉진할 수도 있습니다.
예: 허위 콘텐츠 생성에 사용될 관련 모델 및 애플리케이션.
제한 사항: 이 작업의 주요 제한 사항은 더 큰 규모의 행렬 곱셈(선형 레이어)을 사용하여 대형 모델을 가속화할 수만 있고 컨벌루션 레이어는 가속화할 수 없다는 것입니다.
게다가 제안한 방법은 OPT-175B와 같은 초대형 모델에는 잘 적용되지 않습니다.
우리가 아는 한, INT8 훈련조차도 이러한 초대형 모델의 경우 여전히 해결되지 않은 문제입니다.
위 내용은 Tsinghua Zhu Jun 팀의 새로운 작업: 4자리 정수를 사용하여 Transformer를 훈련합니다. 이는 FP16보다 2.2배, 35.1% 더 빠르며 AGI의 도래를 가속화합니다!의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
