70년 전 시험을 피하고 싶었지만 인터넷 전체에 영향을 미쳤다.

시험을 치르고 싶지 않은 학생의 '고의'가 나중에 인터넷 전체에 영향을 미칠 것이라고 누가 생각이나 했을까요?

70년 전 MIT의 정보 이론 수업에서 한 교사가 학생들의 스트레스를 '줄이기' 위해 객관식 문제를 던졌습니다.

최종 시험에 응시하거나 기존 알고리즘을 개선하는 논문을 작성하는 것은 귀하의 선택입니다.

선생님의 이름은 Robert Fanno였습니다. 그가 학생들에게 말하지 않은 것은 이 "기존 알고리즘"이 바로 그가 정보 이론의 창시자인 Shannon과 공동 집필한 Shannon-Fanno 코딩이라는 것이었습니다. 알고리즘의 단점을 개선하기 위해 본인도 연구에 많은 시간을 투자했다.

(선생님 내부 OS : 그럴 줄은 몰랐네요.)

좀 해롭긴 하지만 이 방법은 정말 효과가 있어요. 이 그룹의 학생들은 "hand in a paper"라는 말을 듣자마자 시험을 볼 필요가 없었고 머리를 긁적인 후 논문을 쓰기로 결정했습니다. 그 중에는 David Huffman도 포함됩니다.

선택하지 않으면 알 수 없지만 선택하면 충격을 받을 것입니다. 이제 막 공부를 시작한 Huffman은 선생님이 파놓은 함정을 빨리 깨달았습니다. 이 논문은 해결하기가 너무 어려웠습니다.

이 글을 쓰는 데 몇 달이 걸렸고, 어려움을 겪었음에도 불구하고 Huffman은 여전히 ​​아무것도 얻지 못했습니다.

하지만 운명은 때로 참 이상해요. 허프만은 마침내 "시험 건너뛰기"를 포기하고 종이 노트를 쓰레기통에 버리려고 할 때 갑자기 아이디어가 떠올랐습니다! 답이 나타납니다!

허프만은 기존 코딩에 대한 연구를 포기하고 새로운 탐구로 방향을 틀었고, 마침내 순서형 주파수 이진 트리 코딩에 기반한 방법을 발견했습니다.

그가 제안한 이 아이디어의 효율성은 선생님의 방법론을 능가했습니다. 이후 개발에서도 그의 이름을 딴 코딩 방식인 허프만 코딩은 데이터 압축 패러다임을 직접적으로 바꿨습니다.

당시 최종 보고서는 거의 만 번 인용되었습니다.

비효율적인 기존 코딩 방법

1951년 MIT에서 강의하던 Robert Fanno는 정보 이론의 어려운 문제에 대해 생각하고 있었습니다.

숫자, 문자 또는 기타 기호를 표현하기 위해 이진 코드를 효율적으로 사용하는 방법은 무엇일까요?

당시 가장 일반적이고 직접적인 방법은 각 문자에 고유한 이진수를 할당하는 것이었습니다.

예를 들어 문자 A는 01000001로 표현될 수 있어요,! 00100001로 표시되며 각 8자리 숫자는 한 문자에 해당합니다.

이렇게 하면 코드를 쉽게 구문 분석할 수 있지만 효율성은 매우 낮습니다.

모스 부호와 유사한 최적화 방법도 있습니다. 일반적인 문자 E는 단지 점으로 표시되지만, 흔하지 않은 Q는 더 길고 더 힘든 "————··——"가 필요합니다.

이 방법을 사용하면 코드 길이가 달라지고 정보를 이해하기가 쉽지 않으며 전송 중에 문자 사이에 공백을 추가해야 합니다. 그렇지 않으면 다양한 문자 조합을 구별할 수 없습니다.

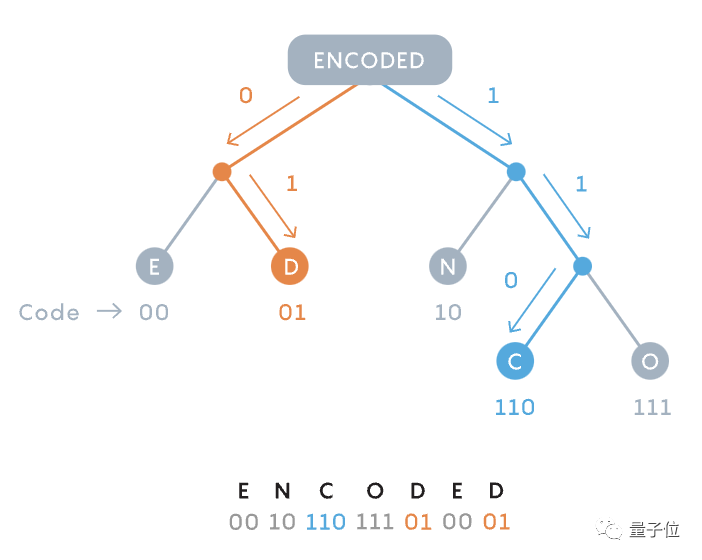
Fanno는 아마도 이 두 가지 방법의 장점이 결합될 수 있다는 것을 깨달았습니다. 즉, 서로 다른 길이의 이진 코드로 문자를 표현하는 것입니다. 게다가 코드 "중복"을 피하기 위해 그는 이진 트리도 구축했습니다.

Pictures

그는 최대 효율성을 위해 각 순열의 가능성을 철저하게 테스트했으며 마침내 효과적인 상황을 얻었습니다.

각 메시지는 빈도에 따라 두 가지로 나누어지며 가능한 한 많이 양면의 문자 사용은 기본적으로 동일합니다.

Pictures

이렇게 하면 일반적으로 사용되는 문자가 더 짧고 밀도가 낮은 가지에 배치됩니다.

1948년 정보 이론의 아버지인 Shannon은 정보 이론을 소개하는 "통신의 수학적 이론"이라는 기사에서 이 방법을 제안했으며, 곧 Fanno도 이를 기술 보고서 ​​형식으로 독자적으로 출판했습니다. 따라서 이 방법을

Shannon-Fano 코딩이라고 합니다.

하지만 이 방법이 항상 효과가 있는 것은 아닙니다. 예를 들어 문자 발생 확률이 {0.35, 0.17, 0.17, 0.16, 0.15}인 경우 이상적인 인코딩을 제공할 수 없습니다.

Fano는 더 나은 압축 전략이 있어야 한다고 믿습니다. 그 이후로 그러한 중요한 임무는 그의 학생들의 손에 맡겨졌습니다.

번뜩이는 영감, 세기의 종이

어쨌든 판노 교수의 방법은 위에서 아래로 캐릭터 트리를 구축하고 가지 쌍 사이에 최대한 대칭을 유지하는 것입니다.

그런 다음 Huffman의 방법은 이 프로세스를 직접적으로 전복시킵니다.

아래에서 위로 이진 트리를 구축합니다.

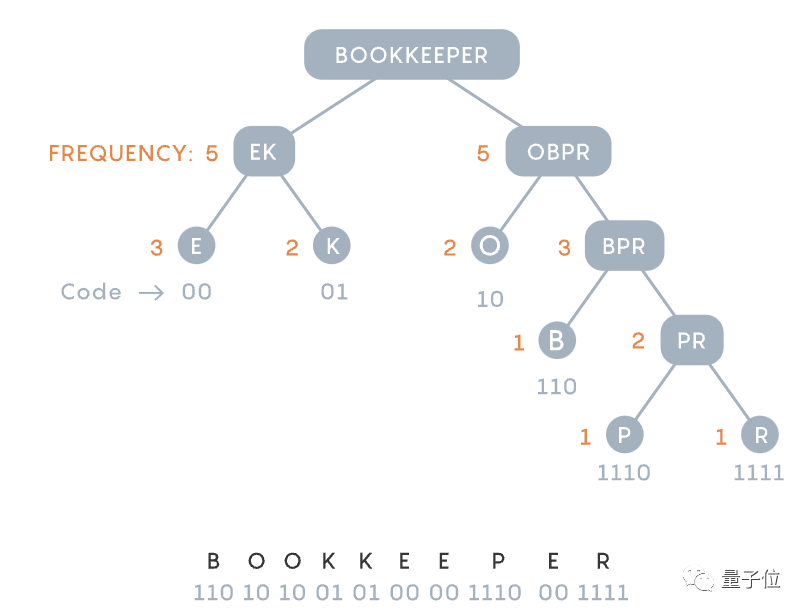
그는 무슨 일이 일어나더라도 유효한 코드 조각에서는

가장 흔한 두 문자가 가장 긴 코드 두 개를 가져야 한다고 믿었습니다.

먼저 공통성이 가장 낮은 두 문자를 식별하고 이를 분기 쌍으로 결합한 다음 프로세스를 반복하여 나머지 문자와 방금 구성한 문자 쌍(쌍)에서 가장 공통적이지 않은 문자를 찾습니다.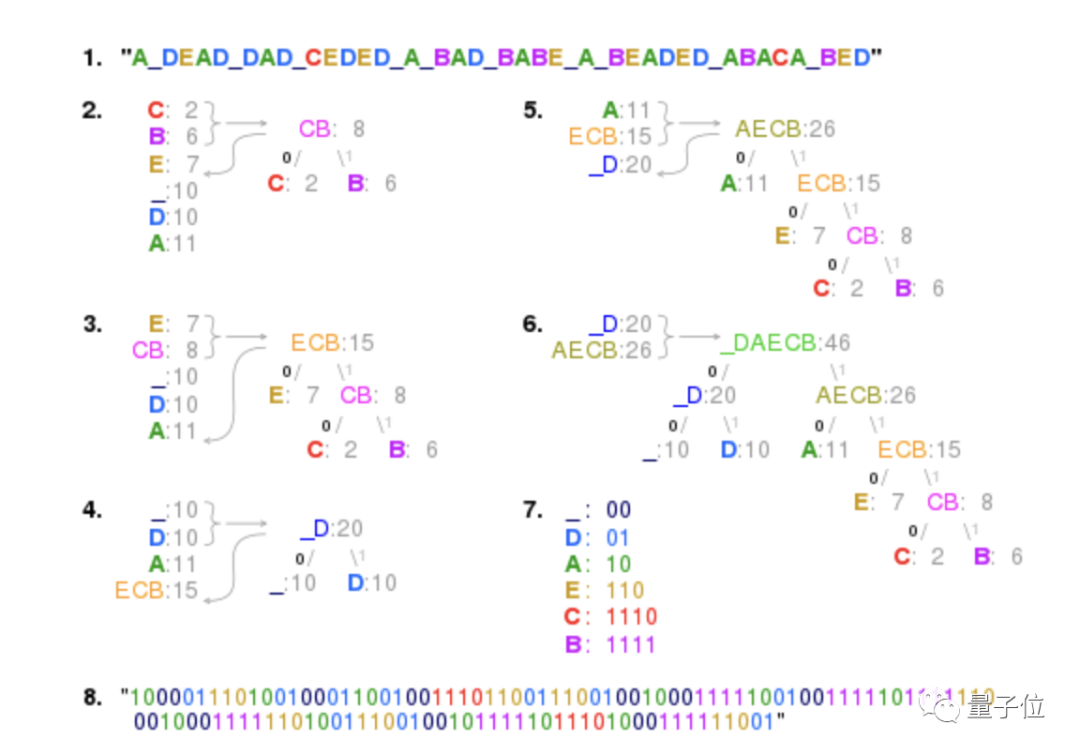

Picture

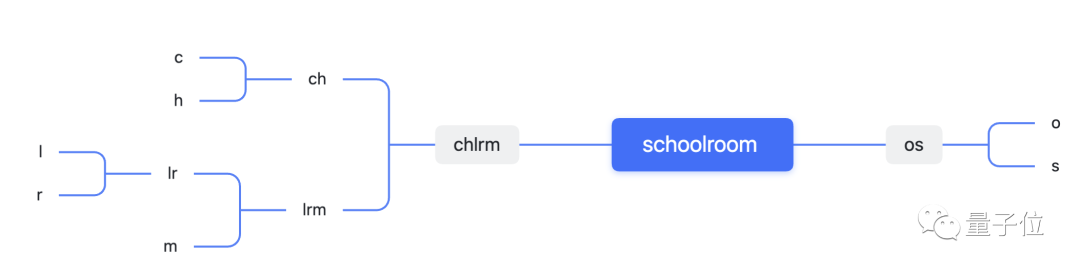
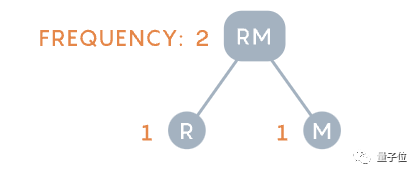
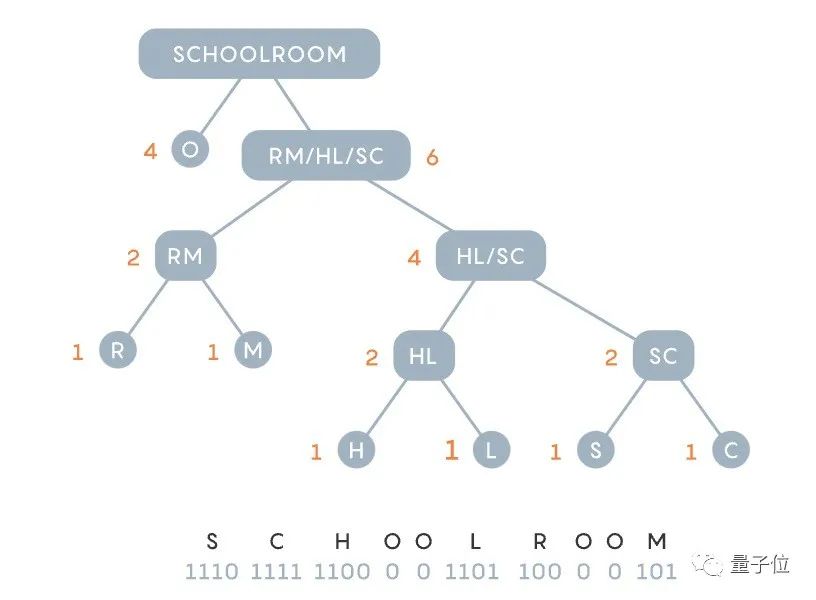
O가 4번 나타나고 S, C, H, L, R, M이 각각 한 번 나타나는 schoolroom을 예로 들어 보겠습니다.

Fano의 방법은 먼저 왼쪽 분기에 O와 다른 문자를 할당하여 양쪽에서 총 5번의 사용량을 가지며 생성된 코드는 총 27비트가 되도록 하는 것입니다.

Pictures

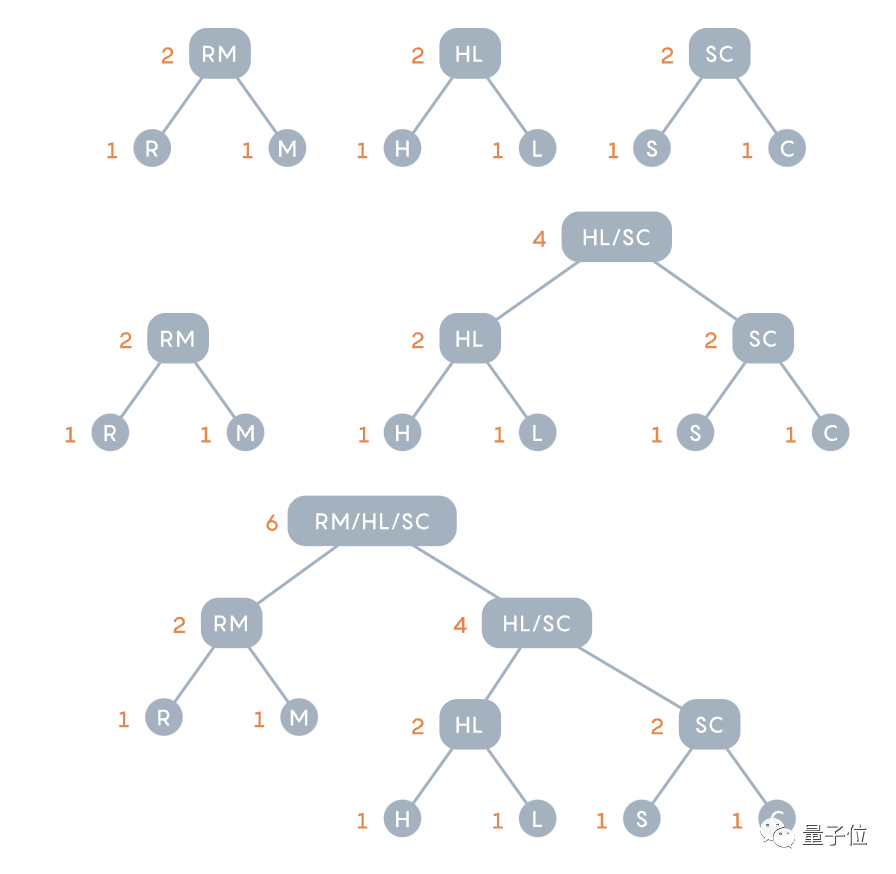
반대로, 예를 들어 Huffman의 방법은 흔하지 않은 r과 m에서 시작하여 이를 문자 쌍으로 결합합니다.

Pictures

결합 후 기존 문자(쌍)에는 O(4회), RM(2회) 및 단일 문자 S, C, H 및 L이 포함됩니다.

발생 빈도에 따라 나누고 이전 작업을 반복합니다. 일반적이지 않은 두 가지 옵션을 그룹화한 다음 숫자 트리와 주파수 다이어그램을 업데이트합니다.

결국 "교실"은 11101111110000110110000101이 되었습니다. 이는 Fano의 하향식 접근 방식보다 1비트 적은입니다.

사진

여기서 1비트는 많지 않지만 수십억 바이트로 확장하면 큰 절약이 됩니다.

사실, 허프만의 방법은 매우 강력한 것으로 입증되었습니다. 구글 학술검색 통계에 따르면, 그 해의 논문은 9570회 인용되었습니다.

Pictures

선생님의 방법은 거의 다시 사용되지 않았습니다.

현재까지 거의 모든 무손실 압축 방식은 이미지, 오디오, 테이블 등을 압축할 수 있는 허프만의 방식을 전체적으로 또는 부분적으로 사용하고 있습니다. PNG 이미지 표준부터 유비쿼터스 소프트웨어 PKZip까지 모든 것을 지원합니다.

현대 컴퓨터 과학의 선구자이자 튜링상 수상자인 크누스(Knuth)는 허프만의 업적을 다음과 같이 설명한 적이 있습니다.

컴퓨터 과학 및 데이터 통신 분야에서 허프만 코딩은 사람들이 사용해 온 기본 아이디어입니다.

나중에 허프만은 그 "유레카" 순간을 회상했습니다. 그 당시 그는 종이 노트를 쓰레기통에 버리려던 참이었지만 갑자기 생각이 합쳐졌고 그의 마음속에 답이 떠올랐습니다.

그게 가장 이상했어요. 내 인생의 순간에 있는 일.

번개처럼 갑작스러운 깨달음.

그리고 자신의 교수인 파노가 이 문제로 어려움을 겪고 있다는 것을 알았더라면 25세의 나이에 과감히 뛰어드는 것은커녕 이 문제를 해결하려고 시도하지 않았을 수도 있다고 말했습니다.

성취감과 질서, 수학으로 미술놀이

허프만 코딩은 데이터 압축 패러다임을 바꾸고 많은 영예와 메달을 획득했습니다.

예를 들어, Huffman은 1998년 IEEE Information Theory Society에서 기술 혁신 부문 Golden Jubilee Award를 수상했고, 1999년에는 IEEE(Institute of Electrical and Electronics Engineers)에서 Richard Hamming Medal을 수상했습니다.

그래도 그가 평생 동안 무손실 압축 방식을 발명한 것에 비해 가장 자랑스러웠던 것은 바로 이 박사 논문이었습니다.

제목: 순차 스위칭 회로의 합성.

Picture

Huffman은 MIT에서 박사 과정을 공부하는 동안 순차 스위칭 회로에 대해 논의하는 중요한 논문을 발표했습니다. 당시 허프만은 비동기식 순차 스위칭 회로를 설계하는 방법을 설명한 최초의 학자였으며, 이 이론은 나중에 컴퓨터 개발에 중요한 논리적 뒷받침을 제공했습니다. 이 논문의 출판으로 그는 프랭클린 연구소로부터 Louis E. Levy 메달을 획득하는 데 도움이 되었을 뿐만 아니라 자연스럽게 학교에 계속 다니면서 스위칭 회로에 대한 강의를 할 수 있는 자격도 얻게 되었습니다.

PicturesHuffman은 학교에 있는 동안 정보 손실 없이

이진수 시퀀스를 다른 이진수 시퀀스

로 변환할 수 있는 혁신적인 수학 공식을 제안했습니다. 이 연구는 당시 중요한 역할을 하여 그를 얻었습니다. 중요한 위치.

당시 벨 연구소 연구 부사장이었던 윌리엄 O. 베이커(William O. Baker)는 국가 안보국(National Security Agency)의 미래 기술 계획 검토를 주로 담당하는 검토 위원회에 그를 채용했습니다. 베이커 박사는 아이젠하워, 케네디, 존슨, 닉슨, 레이건 등 5명의 대통령에게 과학 고문을 역임했습니다.

1967년 이미 정교수였던 호프만은 MIT를 떠나 UCSC(University of California, Santa Cruz)에 입학하기로 결정했다. 학업 과정을 통해 컴퓨터 과학과의 후속 발전을 위한 중요한 기반을 마련합니다.

수학은 허프만의 평생 추구 중 하나라고 할 수 있으며, 나중에 예술에 종사했을 때 수학 없이는 할 수 없었습니다.

Pictures

Huffman은 1970년대부터 종이접기에 큰 관심을 가지게 되었습니다. 그는 동시에 수학과 종이접기 미술을 공부하고 수백 개의 곡선 종이접기 작품을 제작했으며 곡선 종이접기의 수학적 특성을 분석하는 논문 을 출판했습니다. , 종이접기 수학 분야의 선구자가 되어 보세요.

돌아보면, 허프만은 평생 동안 수많은 영예와 표창을 받았지만, 자신의 발명품에 대해 단 한 번도 특허를 신청한 적이 없습니다.

마지막으로 허프만 본인의 명언을 빌리겠습니다.

과학자이자 교사로서 저는 정말 끈기있습니다. 문제에 대한 가장 간단한 해결책을 찾지 못했다고 느끼면 매우 불만족스러워지고 이러한 불만은 최선의 해결책을 찾을 때까지 계속됩니다. 나에게는 이것이 과학자의 본질이다.

위 내용은 70년 전 시험을 피하고 싶었지만 인터넷 전체에 영향을 미쳤다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!