Java에서 그래프 순회를 구현하는 방법-java지도 시간-php.cn

1. 그래프 순회

그래프의 특정 정점에서 시작하여 그래프의 나머지 정점을 방문하며 각 정점은 한 번만 방문합니다.

그래프 순회에는 깊이 우선 순회 DFS와 너비 우선 순회 두 가지 유형이 있습니다. traversal BFS

2. 깊이 우선 순회

깊이 우선 순회는 간단히 말해서 매번 끝으로 이동하는 것을 의미합니다. 이진 트리의 선주문 순회와 유사합니다.

아이디어:

1. 특정 정점에서 시작하여 깊이 우선 순회를 수행하고 정점을 방문한 것으로 표시합니다.

2 정점에서 시작하는 경로를 선택합니다. 그리고 방문한 정점을 표시합니다

3. 2단계에서 끝까지 탐색한 후 다시 이전 정점으로 돌아가서 2단계를 반복합니다.

4. 모든 정점 탐색 종료

이는 재귀적 프로세스임을 알 수 있습니다. 실제로 DFS는 기본적으로 역추적과 동일합니다.

순회:

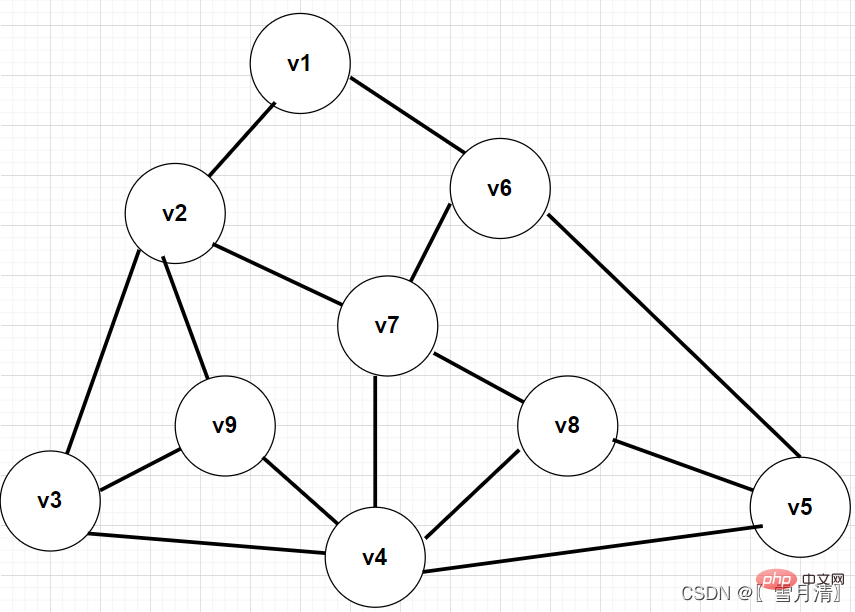
Java에서 그래프 순회를 구현하는 방법

이 그림을 예로 들어 깊이 우선 순회를 수행하세요.

static void dfs(int[][] graph,int idx,boolean[]visit) { int len = graph.length; //访问过 if(visit[idx]) return; //访问该顶点 System.out.println("V"+idx); //标志顶点 visit[idx] = true; for(int i = 1;i < len;i++) { //访问该顶点相连的所有边 if(graph[idx][i] == 1) { //递归进行dfs遍历 dfs(graph, i, visit); } } }

로그인 후 복사

순회 결과:

V1

V2

V3

V4

V 5

V6

V7

V8

V9

그래프를 생성하는 코드:

public static void main(String[] args) { Scanner scanner = new Scanner(System.in); //顶点数 以1开始 int n = scanner.nextInt(); int[][] graph = new int[n+1][n+1]; //边数 int m = scanner.nextInt(); for(int i = 1;i <= m;i++) { int v1 = scanner.nextInt(); int v2 = scanner.nextInt(); graph[v1][v2] = 1; graph[v2][v1] = 1; } //标记数组 false表示未访问过 boolean[] visit = new boolean[n+1]; dfs(graph, 1, visit); }

로그인 후 복사

3. DFS를 사용하여 유향 그래프에 사이클이 있는지 확인

아이디어: 이전 정점에 추가되는 경우 특정 정점을 횡단할 때 , 방문했던 다른 연결된 정점이 있다면 주기가 있어야 합니다

//默认无环 static boolean flag = false; public static void main(String[] args) { Scanner scanner = new Scanner(System.in); //顶点数 以1开始 int n = scanner.nextInt(); int[][] graph = new int[n+1][n+1]; //边数 int m = scanner.nextInt(); for(int i = 1;i <= m;i++) { int v1 = scanner.nextInt(); int v2 = scanner.nextInt(); graph[v1][v2] = 1; } //标记数组 true为访问过 boolean[] visit = new boolean[n+1]; dfs(graph, 1, visit,1); if(flag) System.out.println("有环"); } static void dfs(int[][] graph,int idx,boolean[]visit,int parent) { int len = graph.length; System.out.println("V"+idx); //标记顶点 visit[idx] = true; for(int i = 1;i < len;i++) { //访问该顶点相连的所有边 if(graph[idx][i] == 1) { if( !visit[i] ) { dfs(graph, i, visit,idx); } else if(idx != i) { flag = true; } } } }

로그인 후 복사

참고: 주기가 존재하는지 여부를 확인하는 유향 그래프이고, 주기가 존재하는지 확인하는 무방향 그래프는 의미가 없습니다. 두 기존 경로의 정점은 사이클이 될 수 있습니다

4. 너비 우선 순회

너비 우선 순회는 너비(너비)를 먼저 순회하는 것입니다. 이진 트리의 레벨 순서 순회와 유사합니다.

아이디어:

1. 특정 꼭지점에서 시작하여 너비 우선 순회를 수행하고 해당 꼭지점을 방문한 것으로 표시합니다.

2. 방문하지 않은 정점을 표시합니다

3. 2단계에서 방문한 정점을 시작점으로 1단계와 2단계를 반복합니다.

4. 모든 정점 순회 종료

큐를 사용하여 순회를 지원합니다. queue 큐 순서는 너비 우선 순회입니다. 결과

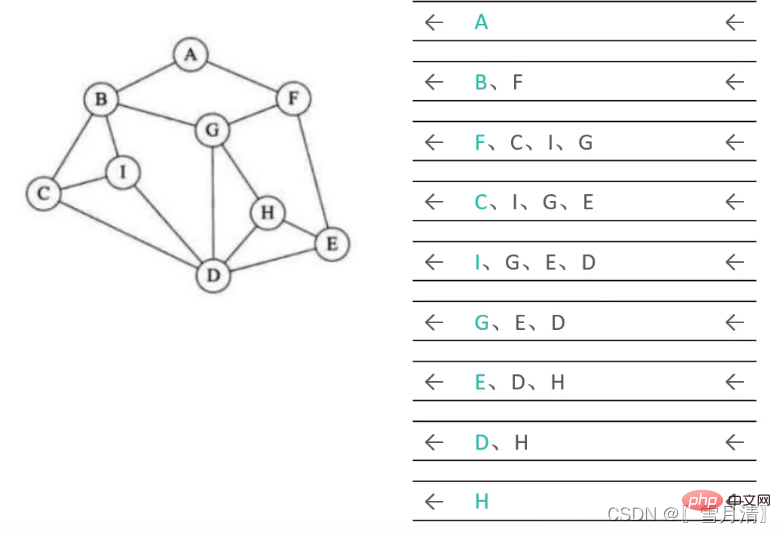
Java에서 그래프 순회를 구현하는 방법

Traversal

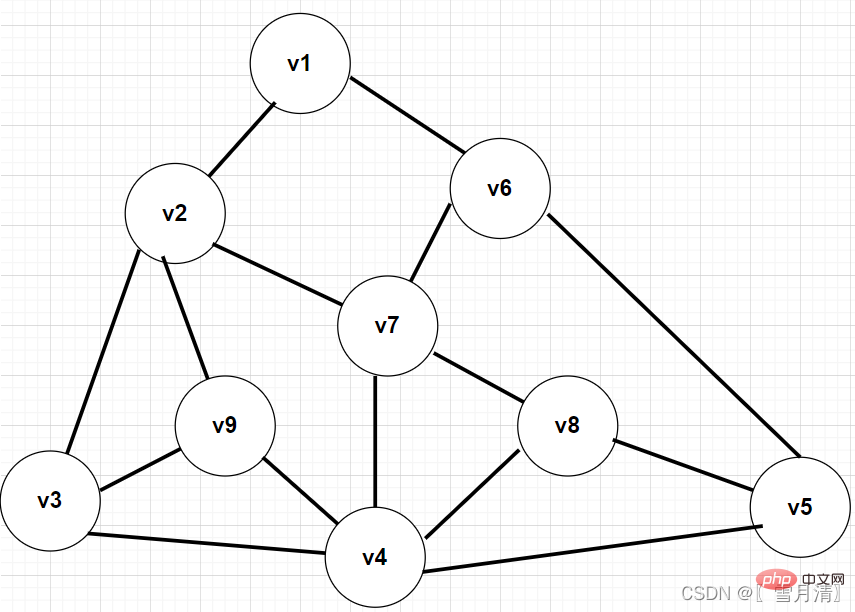
Java에서 그래프 순회를 구현하는 방법

이 그림을 예로 들어, 인접 행렬을 사용하여 그래프를 생성하고 BFS 순회를 수행합니다

static void bfs(int[][] graph) { int len = graph.length; //标记数组 false表示未访问过 boolean[] visit = new boolean[len]; //辅助队列 Queue queue = new LinkedList<>(); queue.offer(1); visit[1] = true; while(!queue.isEmpty()) { int num = queue.poll(); System.out.println("V"+num); //遍历该顶点所有相连顶点 for(int i = 1;i < len;i++) { //相连并且没有被访问过 if(graph[num][i] == 1 && !visit[i]) { queue.offer(i); visit[i] = true; } } } }

로그인 후 복사

Traversal 결과:

V1

V2

V6

V3

V7

V9

V5

V4

V8

그래프를 생성하는 코드

public static void main(String[] args) { Scanner scanner = new Scanner(System.in); //顶点数 以1开始 int n = scanner.nextInt(); int[][] graph = new int[n+1][n+1]; //边数 int m = scanner.nextInt(); for(int i = 1;i <= m;i++) { int v1 = scanner.nextInt(); int v2 = scanner.nextInt(); graph[v1][v2] = 1; graph[v2][v1] = 1; } bfs(graph); }

로그인 후 복사

위 내용은 Java에서 그래프 순회를 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!