
이진 트리 검색은 검색 효율성이 매우 높지만, 이진 트리를 검색하면 다음과 같은 극단적인 상황이 발생합니다. 
이러한 이진 트리의 검색 효율성은 연결 목록보다 훨씬 낮습니다. 검색 이진 트리를 기반으로 나타나는 균형 이진 트리(AVL 트리)가 이 문제를 해결합니다. 균형 이진 트리(AVL 트리)에서 노드의 왼쪽 하위 트리와 오른쪽 하위 트리 간 높이 차이의 절대값이 1보다 큰 경우 회전 작업을 통해 높이 차이가 줄어듭니다.
AVL 트리는 본질적으로 이진 검색 트리입니다. 그 특성은 다음과 같습니다.
자체는 우선 이진 검색 트리입니다. 二叉搜索树。
每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
当插入一个节点或者删除一个节点时,导致某一个节点的左右子树高度差的绝对值大于1,这时需要通过左旋和右旋的操作使二叉树再次达到平衡状态。
平衡因子(balanceFactor)
一个结点的左子树与右子树的高度之差。
AVL树中的任意结点的BF只可能是-1,0和1。
下面是AVL树需要的简单方法和属性:
public class AVLTree <E extends Comparable<E>>{
class Node{
E value;
Node left;
Node right;
int height;
public Node(){}
public Node(E value){
this.value = value;
height = 1;
left = null;
right = null;
}
public void display(){
System.out.print(this.value + " ");
}
}
Node root;
int size;
public int size(){
return size;
}
public int getHeight(Node node) {
if(node == null) return 0;
return node.height;
}
//获取平衡因子(左右子树的高度差,大小为1或者0是平衡的,大小大于1不平衡)
public int getBalanceFactor(){
return getBalanceFactor(root);
}
public int getBalanceFactor(Node node){
if(node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
//判断一个树是否是一个平衡二叉树
public boolean isBalance(Node node){
if(node == null) return true;
int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
if(balanceFactor > 1) return false;
return isBalance(node.left) && isBalance(node.right);
}
public boolean isBalance(){
return isBalance(root);
}
//中序遍历树
private void inPrevOrder(Node root){
if(root == null) return;
inPrevOrder(root.left);
root.display();
inPrevOrder(root.right);
}
public void inPrevOrder(){
System.out.print("中序遍历:");
inPrevOrder(root);
}}往一个树右子树的右子树上插入一个节点,导致二叉树变得不在平衡,如下图,往平衡二叉树中插入5,导致这个树变得不再平衡,此时需要左旋操作,如下: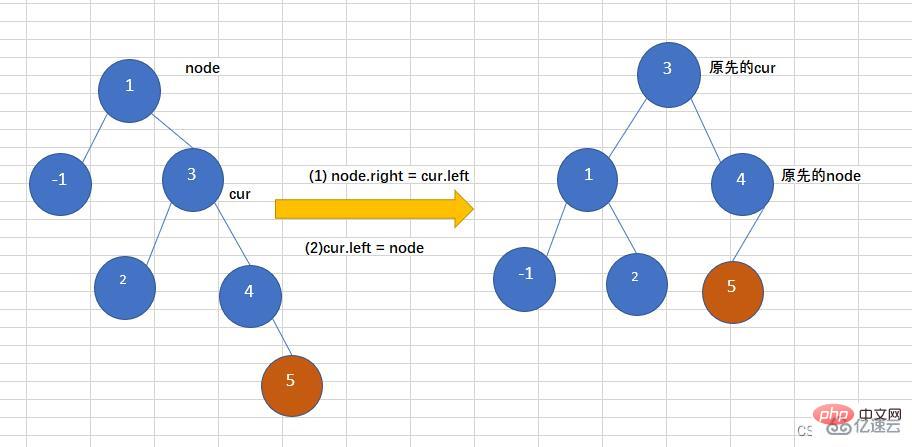
代码如下:
//左旋,并且返回新的根节点
public Node leftRotate(Node node){
System.out.println("leftRotate");
Node cur = node.right;
node.right = cur.left;
cur.left = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}往一个AVL树左子树的左子树上插入一个节点,导致二叉树变得不在平衡,如下图,往平衡二叉树中插入2,导致这个树变得不再平衡,此时需要左旋操作,如下: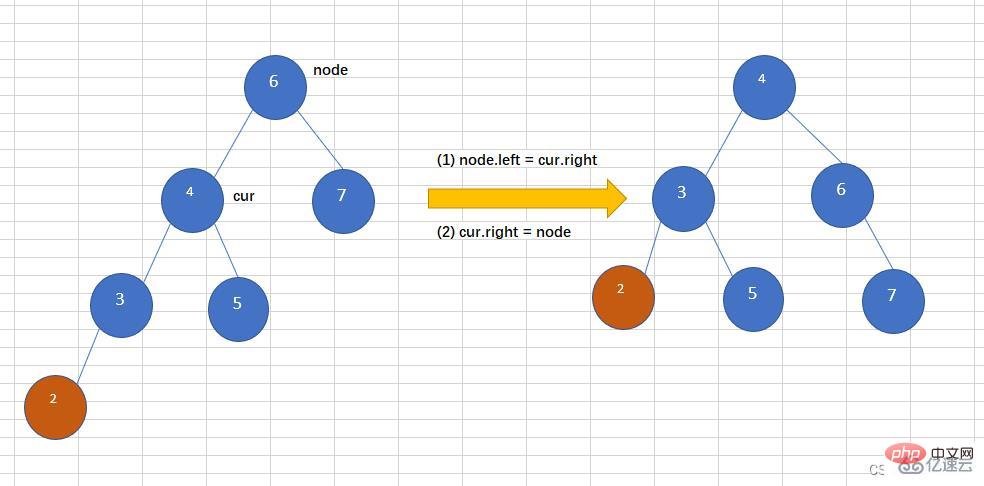
代码如下:
//右旋,并且返回新的根节点
public Node rightRotate(Node node){
System.out.println("rightRotate");
Node cur = node.left;
node.left = cur.right;
cur.right = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}往AVL树左子树的右子树上插入一个节点,导致该树不再平衡,需要先对左子树进行左旋,再对整棵树右旋,如下图所示,插入节点为5.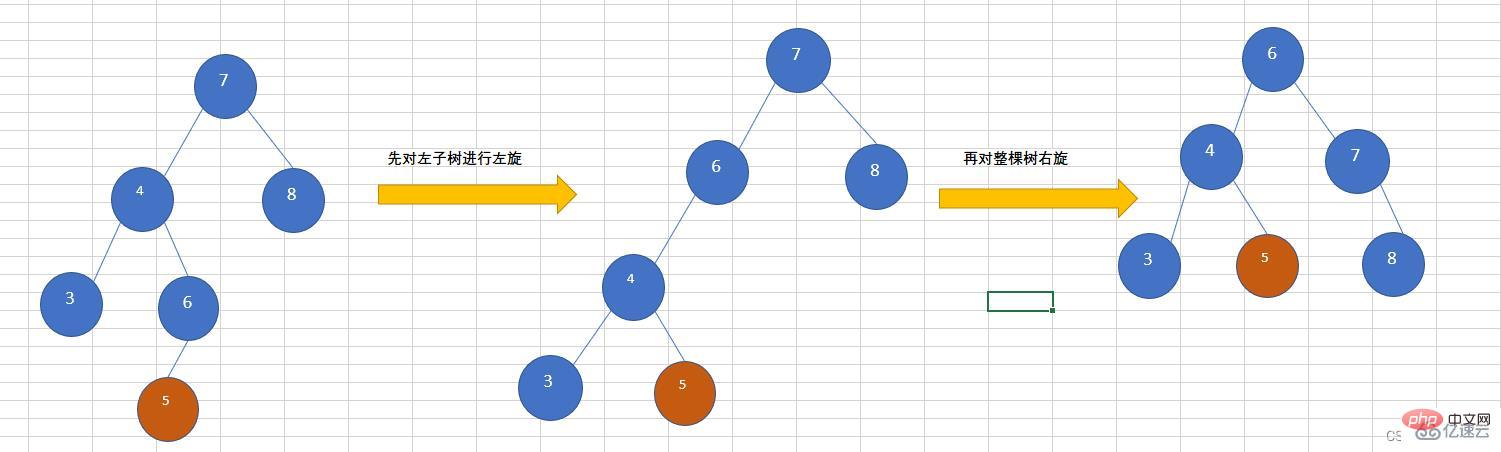
往AVL树右子树的左子树上插入一个节点,导致该树不再平衡,需要先对右子树进行右旋,再对整棵树左旋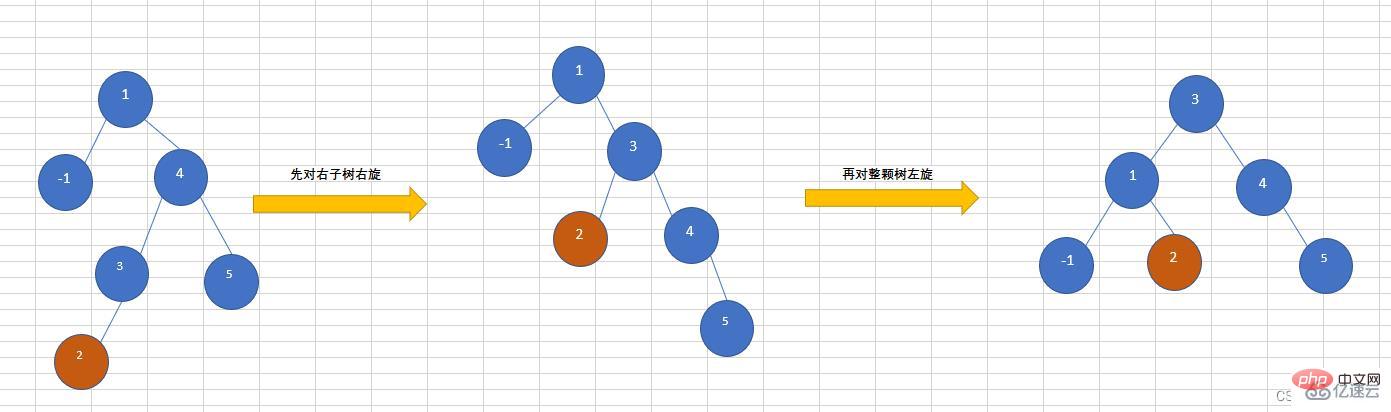
각 노드의 왼쪽 및 오른쪽 하위 트리 높이 차이의 절대값(균형 요소)은 최대 1입니다. 즉, AVL 트리는 본질적으로 균형 함수를 갖는 이진 검색 트리(이진 정렬 트리, 이진 검색 트리)입니다.
왼쪽 회전 및 오른쪽 회전이 필요합니다. 회전 작업은 이진 트리가 다시 균형 잡힌 상태에 도달하도록 합니다. <h3></li></ol></h3><strong>균형 요소(balanceFactor)</strong>🎜<ul class=" list-paddingleft-2">🎜🎜노드의 왼쪽 하위 트리와 오른쪽 하위 트리< code>높이 차이. 🎜🎜🎜AVL 트리에 있는 모든 노드의 BF는 -1, 0 및 1만 될 수 있습니다. 🎜🎜기본 디자인🎜🎜다음은 AVL 트리에 필요한 간단한 메서드와 속성입니다. 🎜//添加元素
public void add(E e){
root = add(root,e);
}
public Node add(Node node, E value) {
if (node == null) {
size++;
return new Node(value);
}
if (value.compareTo(node.value) > 0) {
node.right = add(node.right, value);
} else if (value.compareTo(node.value) < 0) {
node.left = add(node.left, value);
}
//跟新节点高度
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
//获取当前节点的平衡因子
int balanceFactor = getBalanceFactor(node);
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上,此时需要进行右旋
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上,此时需要进行左旋
else if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return leftRotate(node);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上,此时需要先对左子树左旋,在整个树右旋
else if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
//balanceFactor < -1 && getBalanceFactor(node.left) > 0
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上,此时需要先对右子树右旋,再整个树左旋
else if(balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
} 🎜 코드는 다음과 같습니다. 🎜
🎜 코드는 다음과 같습니다. 🎜 //删除节点
public E remove(E value){
root = remove(root,value);
if(root == null){
return null;
}
return root.value;
}
public Node remove(Node node, E value){
Node retNode = null;
if(node == null)
return retNode;
if(value.compareTo(node.value) > 0){
node.right = remove(node.right,value);
retNode = node;
}
else if(value.compareTo(node.value) < 0){
node.left = remove(node.left,value);
retNode = node;
}
//value.compareTo(node.value) = 0
else{
//左右节点都为空,或者左节点为空
if(node.left == null){
size--;
retNode = node.right;
}
//右节点为空
else if(node.right == null){
size--;
retNode = node.left;
}
//左右节点都不为空
else{
Node successor = new Node();
//寻找右子树最小的节点
Node cur = node.right;
while(cur.left != null){
cur = cur.left;
}
successor.value = cur.value;
successor.right = remove(node.right,value);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
if(retNode == null)
return null;
//维护二叉树平衡
//跟新height
retNode.height = Math.max(getHeight(retNode.left),getHeight(retNode.right));
}
int balanceFactor = getBalanceFactor(retNode);
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上,此时需要进行右旋
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上,此时需要进行左旋
else if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
return leftRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上,此时需要先对左子树左旋,在整个树右旋
else if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上,此时需要先对右子树右旋,再整个树左旋
else if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
} 🎜 코드는 다음과 같습니다. 🎜rrreee🎜LR(먼저 좌회전한 다음 오른쪽으로 회전)🎜🎜AVL 트리의
🎜 코드는 다음과 같습니다. 🎜rrreee🎜LR(먼저 좌회전한 다음 오른쪽으로 회전)🎜🎜AVL 트리의 오른쪽 하위 트리에 노드를 삽입합니다. 왼쪽 하위 트리로 인해 트리가 더 이상 균형을 이루지 못하게 됩니다. 먼저 왼쪽 하위 트리에서 왼쪽 회전을 수행한 다음 전체 트리를 오른쪽 회전해야 합니다. code>에 아래 그림과 같이 노드 5를 삽입합니다.🎜오른쪽 하위 트리의 왼쪽 하위 트리로 이동 노드를 삽입하면 트리가 더 이상 균형을 이루지 않게 됩니다. 먼저 오른쪽 하위 트리를 오른쪽으로 회전한 다음 전체 트리를 왼쪽으로 회전해야 합니다. 아래 그림과 같이 삽입된 노드는 2.🎜🎜입니다. 🎜🎜노드 추가🎜rrreee🎜노드 삭제🎜rrreee위 내용은 Java 데이터 구조 AVL 트리 예제 분석의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!