오늘은 2023.1년 arixv에 올라온 다변량 시계열 예측 글을 소개해드리고자 합니다. 출발점이 꽤 흥미롭습니다. 다변량 시계열의 공정성을 향상시키는 방법입니다. 본 논문에서 사용된 모델링 방법은 시공간 예측, Domain Adaptation 등에서 사용되었던 기존의 연산을 모두 사용하였지만, 다변수 공평성의 점은 비교적 새로운 것이다.

공정성 문제는 기계 학습 분야의 거시적 개념입니다. 기계 학습의 공정성에 대한 한 가지 이해는 다양한 샘플에 대한 모델 피팅 효과의 일관성입니다. 모델이 일부 표본에서는 잘 수행되고 다른 표본에서는 성능이 좋지 않으면 모델의 공정성이 떨어집니다. 예를 들어, 일반적인 시나리오는 추천 시스템에서 헤드 샘플에 대한 모델의 예측 효과가 꼬리 샘플의 예측 효과보다 더 우수하다는 것입니다. 이는 다양한 샘플에 대한 모델 예측 효과의 불공평성을 반영합니다.
다변량 시계열 예측 문제로 돌아가서, 공정성은 모델이 각 변수에 대해 더 나은 예측 효과를 갖는지 여부를 나타냅니다. 다양한 변수에 대한 모델의 예측 효과가 매우 다른 경우 이 다변량 시계열 예측 모델은 불공평합니다. 예를 들어 아래 그림의 예에서 표의 첫 번째 행은 각 변수에 대한 다양한 모델의 예측 효과에 대한 MAE의 분산입니다. 다양한 모델에는 어느 정도 불공평성이 있음을 알 수 있습니다. 아래 그림의 시퀀스는 예입니다. 일부 시퀀스는 예측이 더 좋고 다른 시퀀스는 예측이 더 나쁩니다.
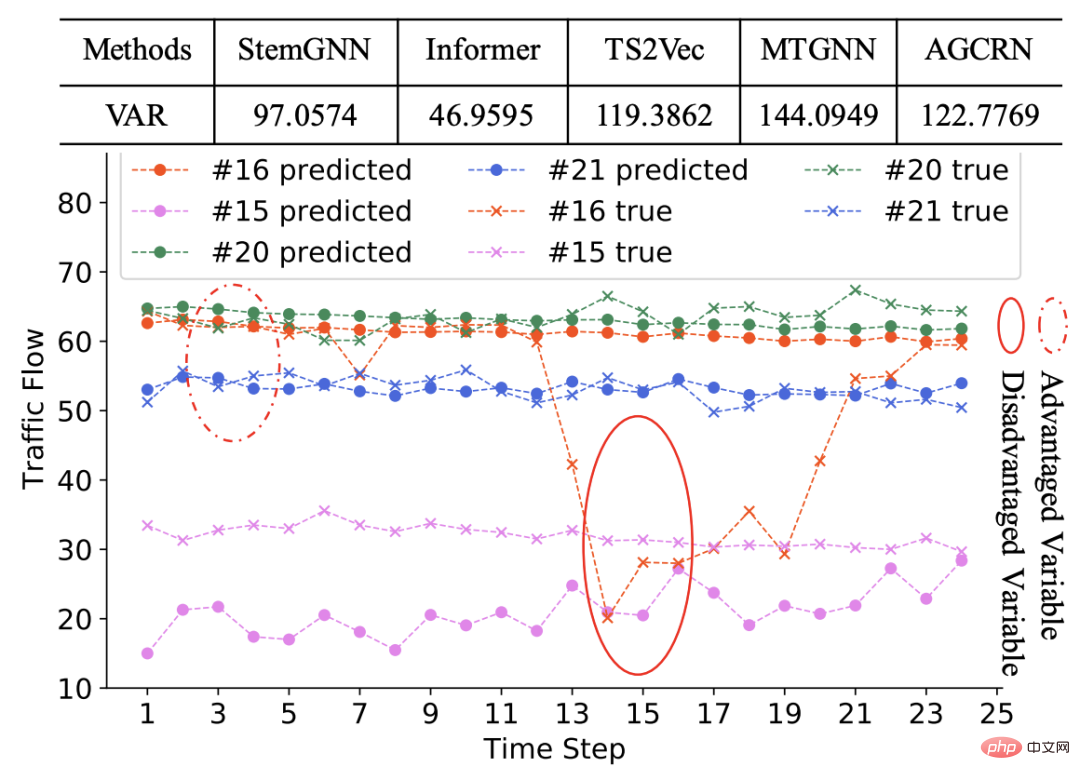
불공정은 왜 발생하는 걸까요? 다변량 시계열이든 다른 기계 학습 분야이든, 서로 다른 샘플의 예측 효과가 크게 달라지는 주요 이유 중 하나는 서로 다른 샘플이 서로 다른 특성을 갖고 모델이 훈련 과정에서 특정 샘플의 특성에 의해 지배될 수 있다는 것입니다. , 그 결과 모델은 훈련을 지배하는 샘플에 대해 잘 예측하지만 지배적이지 않은 샘플에 대해서는 예측이 좋지 않습니다.
다변량 시계열에서는 변수마다 순서 패턴이 매우 다를 수 있습니다. 예를 들어, 위에 표시된 예에서 대부분의 시퀀스는 고정되어 있어 모델 훈련 프로세스를 지배합니다. 소수의 시퀀스가 다른 시퀀스와 다른 변동성을 나타내므로 이러한 시퀀스에 대한 모델의 예측 성능이 저하됩니다.
다변량 시계열의 불공평함을 해결하는 방법은 무엇입니까? 한 가지 생각은, 서로 다른 시퀀스의 서로 다른 특성으로 인해 불공정이 발생하므로, 시퀀스 간의 공통점과 차이점을 독립적으로 분해하여 모델링할 수 있다면 위에서 언급한 문제가 완화될 수 있다는 것입니다.
이 기사는 이 아이디어를 기반으로 합니다. 전체 아키텍처는 클러스터링 방법을 사용하여 다변수 시퀀스를 그룹화하고, 추가로 적대적 학습 방법을 사용하여 원래 표현에서 각 그룹을 떼어내는 것입니다. 정보, 공개 정보를 얻으십시오. 위의 과정을 통해 공개 정보와 시퀀스별 정보가 분리되고, 이 두 부분의 정보를 기반으로 최종 예측이 이루어집니다.
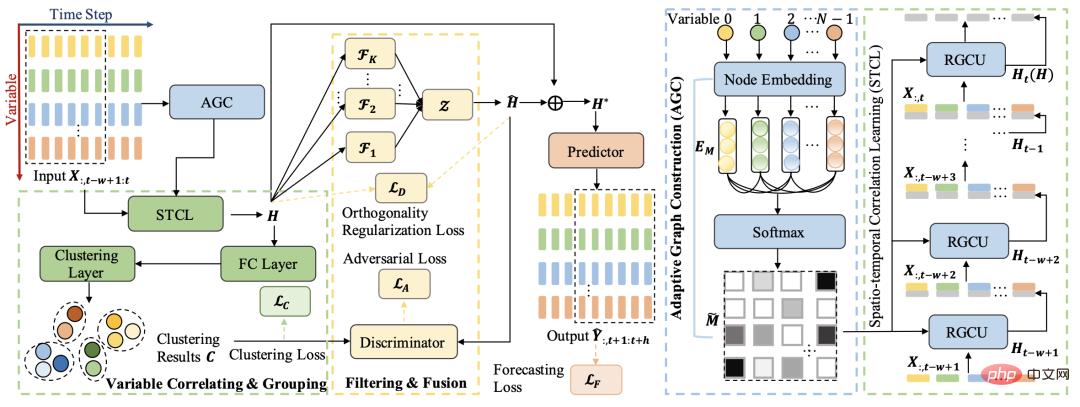
전체 모델 구조는 주로 다변수 시퀀스 관계 학습, 시공간 관계 네트워크, 시퀀스 클러스터링 및 분해 학습의 4개 모듈로 구성됩니다.
다변수 시계열의 핵심 포인트 중 하나는 각 시퀀스 간의 관계를 학습하는 것입니다. 이 기사에서는 공간-시간적 방법을 사용하여 이 관계를 학습합니다. 다변량 시계열은 많은 시공간 예측 작업과 달리 다양한 변수 간의 관계를 미리 정의할 수 있으므로 여기서는 인접 행렬의 자동 학습 방법을 사용합니다. 구체적인 계산 논리는 각 변수에 대해 무작위로 초기화된 임베딩을 생성한 다음 임베딩의 내부 곱과 일부 후처리를 사용하여 두 변수 간의 관계를 인접 행렬의 해당 위치에 있는 요소로 계산하는 것입니다.
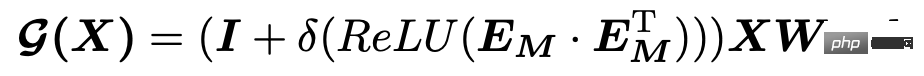
인접 행렬을 자동으로 학습하는 이 방법은 Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks(KDD 2020), REST: Reciprocal Framework for에 표시된 것처럼 시공간 예측에 매우 일반적으로 사용됩니다. 시공간 결합 예측(WWW 2021) 및 기타 기사에서는 이 방법을 채택했습니다. 관심 있는 학생들은 Planet 기사 KDD2020 클래식 시공간 예측 모델 MTGNN 코드 분석에서 관련 모델의 원리 구현을 자세히 소개했습니다.
인접 행렬을 사용하여 기사에서는 그래프 시계열 예측 모델을 사용하여 다변수 시계열을 시공간적으로 인코딩하여 각 변수 시퀀스의 표현을 얻습니다. 구체적인 모델 구조는 DCRNN과 매우 유사하며 GRU를 기반으로 각 단위의 계산에 GCN 모듈이 도입됩니다. 일반 GRU의 각 단위 계산 과정에서 이웃 노드의 벡터가 도입되어 GCN을 수행하여 업데이트된 표현을 얻는 것으로 이해될 수 있습니다. DCRNN의 구현 코드 원리에 대해서는 DCRNN 모델 소스 코드 분석 문서를 참조할 수 있습니다.
각 변수 시계열의 표현을 얻은 후 다음 단계는 이러한 표현을 클러스터링하여 각 변수 시퀀스의 그룹화를 얻은 다음 각 변수 그룹의 고유 정보를 추출하는 것입니다. 이 문서에서는 클러스터링 프로세스를 안내하기 위해 다음 손실 함수를 소개합니다. 여기서 H는 각 변수 시퀀스의 표현을 나타내고 F는 각 변수 시퀀스와 K 범주의 관계를 나타냅니다.
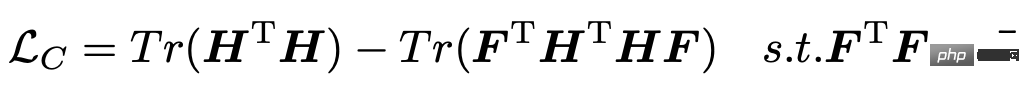
이 손실 함수의 업데이트 프로세스에는 EM 알고리즘의 사용이 필요합니다. 즉, H를 나타내도록 시퀀스를 수정하고 F를 최적화하고 F를 수정하여 H를 최적화합니다. 본 논문에서 채택한 방법은 표현 H를 얻기 위해 여러 라운드의 모델을 훈련시킨 후 SVD를 사용하여 행렬 F를 한 번 업데이트하는 것입니다.
분해 학습 모듈의 핵심은 각 범주 변수의 공개 표현과 비공개 표현을 구별하는 것입니다. 공개 표현은 각 클러스터 변수의 시퀀스가 공유하는 특성을 의미하고 비공개 표현은 각 클러스터 내의 특성. 가변 시퀀스에 고유한 특성입니다. 이 목표를 달성하기 위해 논문에서는 분해 학습과 적대적 학습의 아이디어를 채택하여 각 클러스터의 표현을 원래 시퀀스 표현에서 분리합니다. 클러스터 표현은 각 클래스의 특성을 나타내고, 스트립 표현은 모든 시퀀스의 공통성을 나타냅니다. 이러한 공통 표현을 예측에 사용하면 각 변수를 예측하는 데 공정성을 얻을 수 있습니다.
이 기사에서는 적대 학습 아이디어를 사용하여 공개 표현과 비공개 표현(즉, 클러스터링을 통해 얻은 각 클러스터의 표현) 사이의 L2 거리를 손실 역최적화로 직접 계산하므로 공개 부분 표현과 비공개 표현의 격차는 최대한 넓습니다. 또한, public 표현과 private 표현의 내적을 0에 가깝게 만들기 위해 직교 제약 조건을 추가합니다.
이 기사의 실험은 주로 공정성과 예측 효과의 두 가지 측면에서 비교됩니다. 비교 모델에는 기본 시계열 예측 모델(LSTNet, Informer), 그래프 시계열 예측 모델 등이 포함됩니다. 공정성 측면에서는 다양한 변수에 따른 예측 결과의 분산을 이용하여 비교를 통해 이 방법의 공정성이 다른 모델에 비해 크게 향상되었습니다(아래 표 참조).
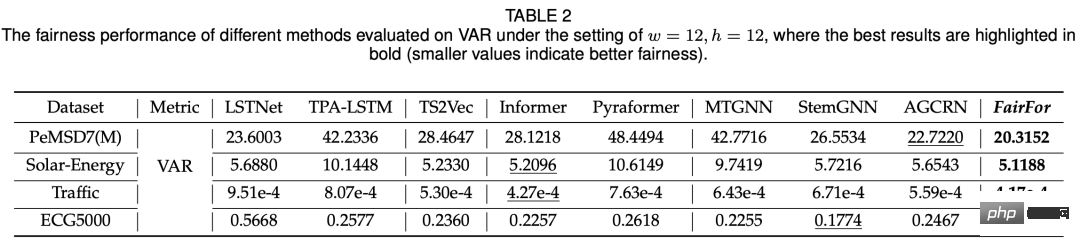
이 기사에서 제안한 모델은 기본적으로 SOTA와 동등한 결과를 얻을 수 있습니다.
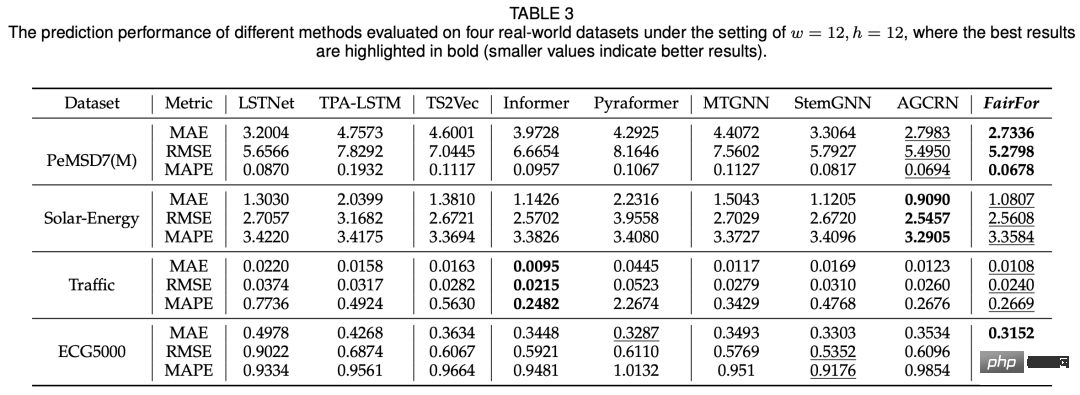
모델의 공정성을 보장하는 방법은 많은 시나리오에서 직면하는 문제입니다. 머신러닝의 . 본 논문에서는 이러한 차원의 문제를 다변량 시계열 예측에 도입하고 시공간 예측 및 적대적 학습 방법을 사용하여 이를 더 잘 해결합니다.
위 내용은 다변량 시계열의 공정성 문제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!