통계 테스트와 기계 학습을 사용하여 태양광 발전 성능 테스트 및 비교 분석 및 예측
이 기사에서는 가설 테스트, 기능 엔지니어링, 시계열 모델링 방법 등을 사용하여 데이터 세트에서 실질적인 가치를 얻는 기술에 대해 설명합니다. 또한 다양한 시계열 모델에 대한 데이터 유출 및 데이터 준비와 같은 문제를 다루고 세 가지 일반적인 시계열 예측에 대한 비교 테스트를 수행할 것입니다.
시계열 예측은 자주 연구되는 주제입니다. 여기서는 두 태양광 발전소의 데이터를 사용하여 법칙을 연구하고 모델링을 수행합니다. 먼저 이러한 문제를 두 가지 질문으로 요약하여 해결하세요.
이 질문에 계속 답하기 전에 먼저 태양광 발전소가 어떻게 전기를 생산하는지 이해해 봅시다.
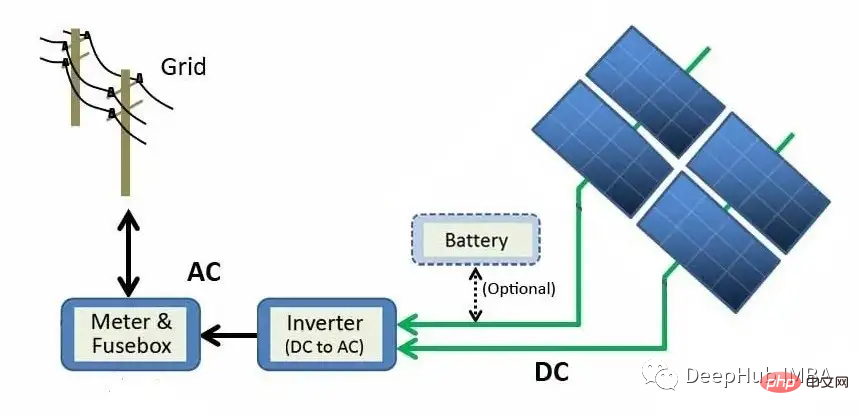
위 다이어그램은 태양광 패널 모듈에서 그리드까지 발전 과정을 설명합니다. 태양 에너지는 광전 효과를 통해 직접 전기 에너지로 변환됩니다. 실리콘(태양광 패널에서 가장 흔한 반도체 재료)과 같은 재료가 빛에 노출되면 광자(전자기 에너지의 아원자 입자)가 흡수되고 자유 전자가 방출되어 직류(DC)를 생성합니다. 인버터를 사용하여 DC 전력을 교류(AC)로 변환한 후 그리드로 보내 가정에 배전할 수 있습니다.
원시 데이터는 각 태양광 발전소에 대한 두 개의 쉼표로 구분된 값(CSV) 파일로 구성됩니다. 한 문서는 발전 과정을 보여주고, 다른 문서는 태양광 발전소의 센서에 의해 기록된 측정값을 보여줍니다. 각 태양광 발전소에 대한 두 개의 데이터 세트는 pandas df로 구성되었습니다.
태양광 발전소 1(SP1)과 태양광 발전소 2(SP2)의 데이터는 2020년 5월 15일부터 2020년 6월 18일까지 15분 간격으로 수집되었습니다. SP1 및 SP2 데이터세트에는 모두 동일한 변수가 포함되어 있습니다.
날씨 센서는 각 태양광 발전소의 주변 온도, 모듈 온도 및 복사량을 기록하는 데 사용됩니다.
이 데이터 세트의 경우 DC 전원이 종속 변수(목표 변수)가 됩니다. 우리의 목표는 성능이 떨어지는 태양광 모듈을 찾는 것입니다.
분석 및 예측을 위한 두 개의 독립적인 df. 유일한 차이점은 예측에 사용되는 데이터는 시간 간격으로 리샘플링되는 반면, 분석에 사용되는 데이터 프레임에는 15분 간격이 포함된다는 점입니다.
먼저 위 질문에 답하는 데 아무런 가치도 추가하지 않는 식물 ID를 제거합니다. 모듈 ID도 예측 데이터 세트에서 제거됩니다. 표 1과 2는 데이터 예를 보여줍니다.


데이터 분석을 계속하기 전에 태양광 발전소에 대해 다음을 포함하여 몇 가지 가정을 했습니다.
데이터 과학을 처음 접하는 사람들에게 EDA는 시각화를 플롯하고 통계 테스트를 수행하여 데이터를 이해하는 중요한 단계입니다. 먼저 SP1과 SP2에 대해 DC와 AC를 플로팅하여 각 태양광 발전소의 성능을 관찰할 수 있습니다.
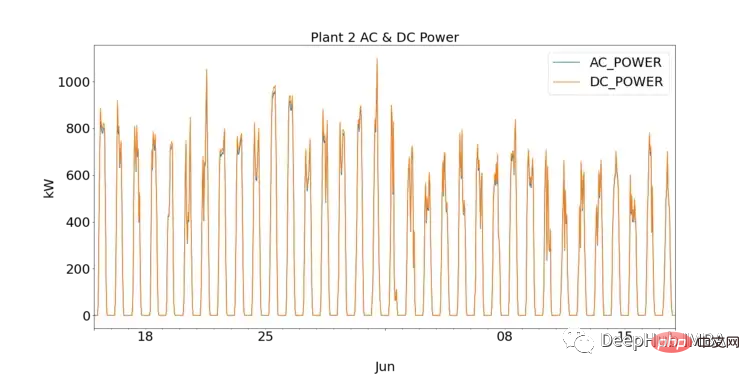
SP1은 sp2보다 훨씬 더 높은 DC 전력을 보여줍니다. SP1에서 수집한 데이터가 정확하고 데이터를 기록하는 데 사용된 기기에 결함이 없다고 가정하면, 이는 SP1의 인버터에 대해 일일 주파수별로 AC 및 DC 전력을 집계하여 더 깊이 연구해야 함을 나타냅니다
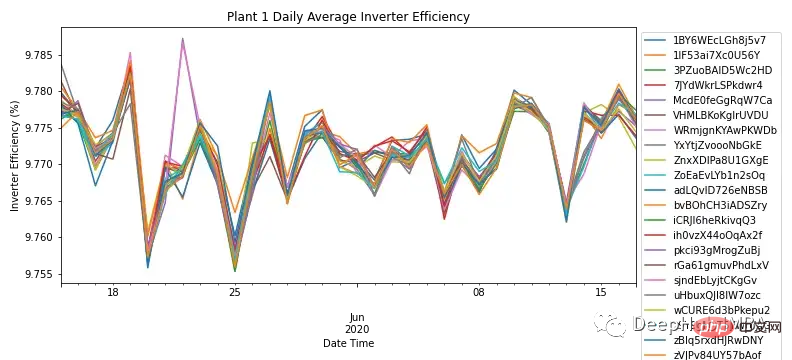
각 모듈, 그림 3은 SP1의 모든 모듈의 인버터 효율을 보여줍니다. 현장 지식에 따르면 태양광 인버터의 효율은 93~96% 사이여야 합니다. 모든 모듈의 효율이 9.76%~9.79%에 달하므로 이는 인버터의 성능을 조사하고 교체해야 하는지 여부를 조사해야 함을 나타냅니다.
SP1에서 인버터에 문제가 나타났기 때문에 추가 분석은 SP2에서만 수행되었습니다.
이 작은 분석은 인버터를 연구하는 데 더 많은 시간을 투자한 결과이지만 태양광 모듈 성능을 결정하는 주요 질문에 대한 답은 아닙니다.
SP2의 인버터가 제대로 작동하기 때문에 데이터를 더 깊이 파고들면 이상 징후를 식별하고 조사할 수 있습니다.
그림 4는 모듈 온도와 주변 온도의 관계를 보여주며, 모듈 온도가 극도로 높은 경우가 있습니다.
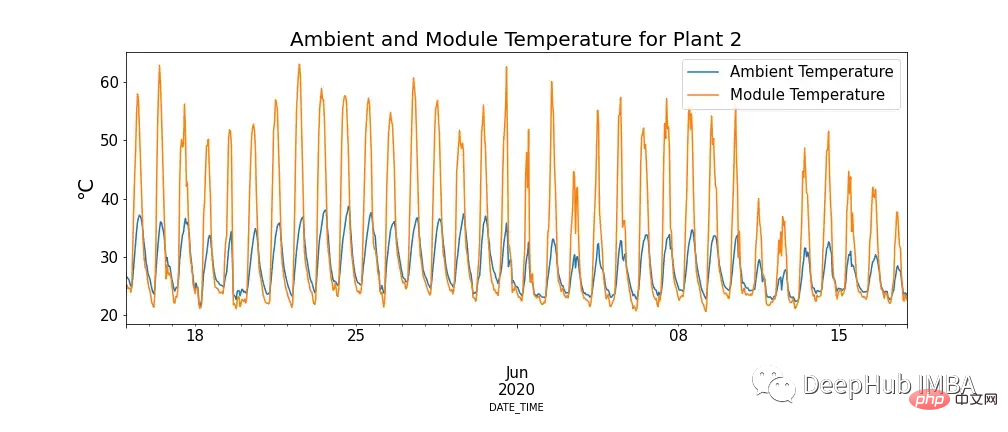
이것은 우리의 지식에 어긋나는 것처럼 보일 수도 있지만 고온은 태양광 패널에 부정적인 영향을 미친다는 것을 알 수 있습니다. 광자가 태양 전지 내의 전자와 접촉하면 자유 전자가 방출되지만 온도가 높아지면 이미 더 많은 전자가 들뜬 상태가 되어 패널이 생성할 수 있는 전압이 감소하여 효율이 감소합니다.
이 현상을 고려하여 아래 그림 5는 SP2의 모듈 온도와 DC 전력을 보여줍니다. (주변 온도가 모듈 온도보다 낮은 데이터 포인트와 모듈이 더 낮은 숫자로 실행되는 시간은 다음과 같이 필터링되었습니다. 데이터 왜곡을 방지합니다).
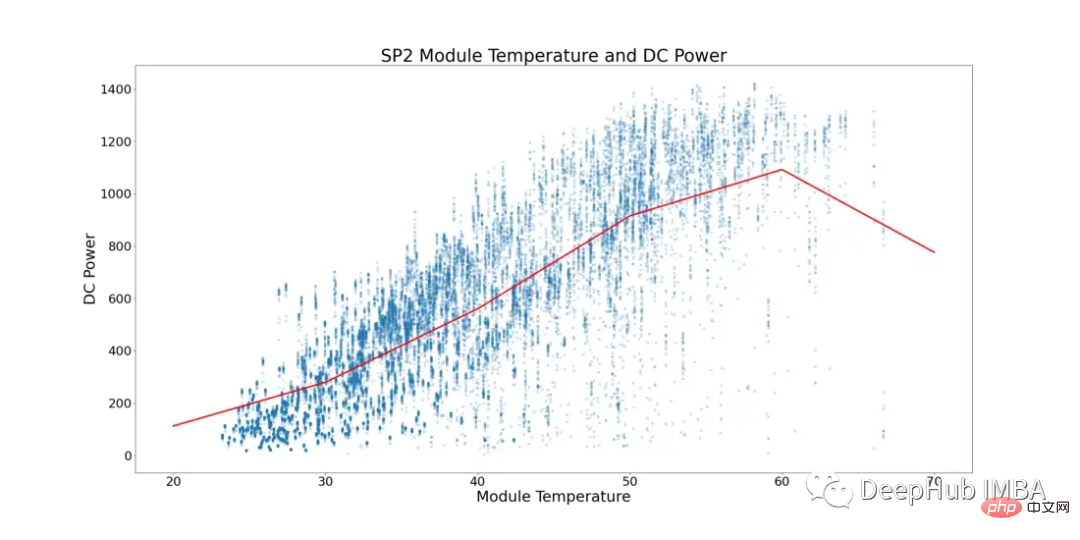
그림 5에서 빨간색 선은 평균 기온을 나타냅니다. 여기서는 명확한 전환점과 DC 전력 정체 징후가 있음을 확인할 수 있습니다. ~52°C에서 정체되기 시작합니다. 성능이 최적이 아닌 태양광 모듈을 찾기 위해 모듈 온도가 52°C를 초과하는 모든 행을 제거했습니다.
아래 그림 6은 하루 동안 SP2의 각 모듈의 DC 전원을 보여줍니다. 이는 기본적으로 기대에 부응하며 정오에는 발전량이 더 커집니다. 그러나 또 다른 문제가 있습니다. 피크 운영 기간에는 발전량이 적습니다. 그날 기상 상황이 좋지 않거나 SP2에 정기적인 유지 관리가 필요할 수 있기 때문에 이러한 상황의 이유를 요약하기는 어렵습니다.
그림 6에도 성능이 낮은 모듈의 징후가 있습니다. 이는 그래프에서 가장 가까운 클러스터에서 벗어나는 모듈(개별 데이터 포인트)로 식별될 수 있습니다.

어떤 모듈의 성능이 저조한지 확인하기 위해 통계 테스트를 수행하면서 각 모듈의 성능을 다른 모듈과 비교하여 성능을 확인할 수 있습니다.
15분마다 서로 다른 모듈의 DC 전원 공급 장치가 동시에 분포하는 것은 가설 테스트를 통해 어떤 모듈의 성능이 좋지 않은지 확인할 수 있습니다. 카운트는 p-값이 0.001 미만인 모듈이 99.9% 신뢰 구간을 벗어나는 횟수입니다.
그림 7은 같은 기간 동안 각 모듈이 다른 모듈보다 통계적으로 유의미하게 낮은 횟수를 내림차순으로 보여줍니다.

그림 7을 보면 'Quc1TzYxW2pYoWX' 모듈에 문제가 있음이 분명합니다. 이 정보는 원인을 조사하기 위해 관련 SP2 직원에게 제공될 수 있습니다.
아래에서는 SARIMA, XGBoost 및 CNN-LSTM의 세 가지 시계열 알고리즘을 사용하여 모델링 및 비교를 시작합니다.
세 가지 모델 모두 Predict를 사용하여 다음 데이터 포인트를 예측합니다. Walk-forward 검증은 시간이 지남에 따라 예측의 정확도가 떨어지기 때문에 시계열 모델링에 사용되는 기술입니다. 따라서 보다 실용적인 접근 방식은 실제 데이터가 제공될 때 모델을 재교육하는 것입니다.
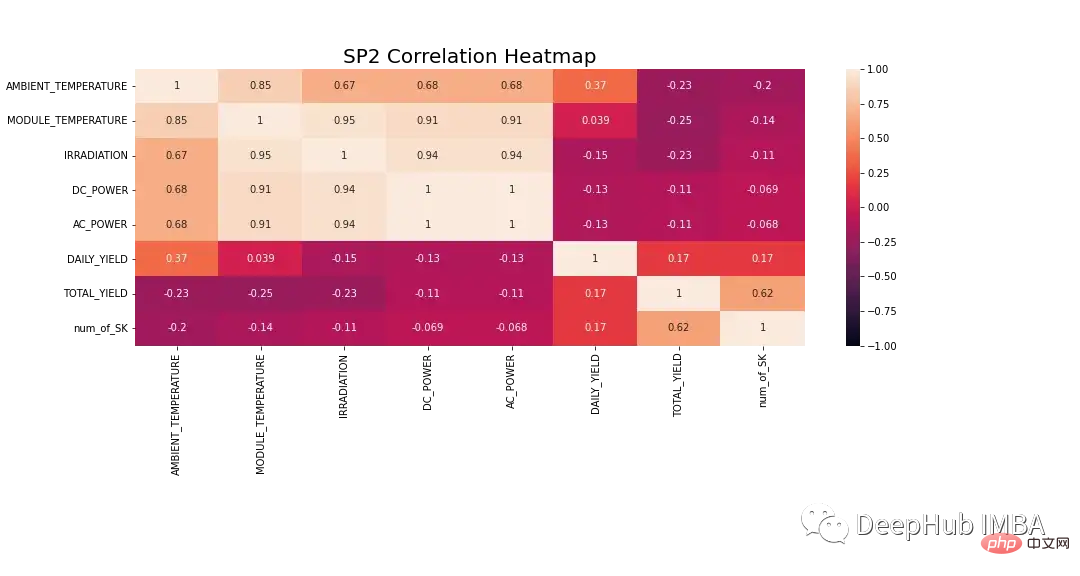
모델링하기 전에 데이터를 더 자세히 연구해야 합니다. 그림 8은 SP2 데이터세트의 모든 기능에 대한 상관관계 히트맵을 보여줍니다. 히트맵은 종속변수인 DC 전력과 모듈 온도, 일사량 및 주변 온도 사이의 강한 상관관계를 보여줍니다. 이러한 특성은 예측에 중요한 역할을 할 수 있습니다.
아래 히트맵에서 AC 전원의 Pearson 상관 계수는 1입니다. 데이터 유출 문제를 방지하기 위해 데이터에서 DC 전원을 제거합니다.
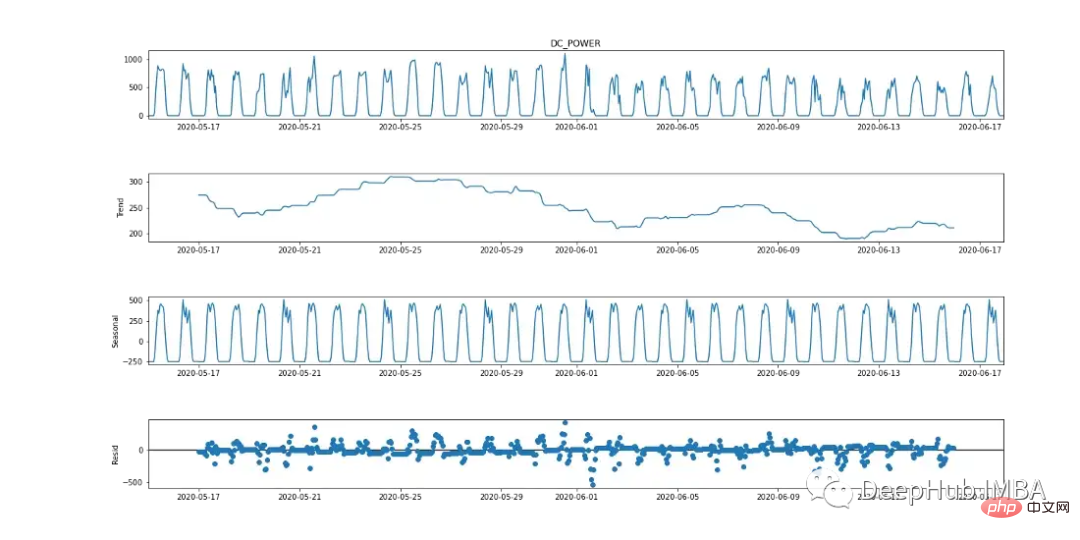
SARIMA(계절 자기회귀 통합 이동 평균)는 일변량 시계열 예측 방법입니다. 목표 변수가 24시간 순환 주기의 징후를 나타내기 때문에 SARIMA는 계절 효과를 고려하므로 효율적인 모델링 옵션입니다. 이는 아래의 계절별 분석 차트에서 확인할 수 있습니다.
SARIMA 알고리즘에는 데이터가 고정되어 있어야 합니다. 통계 테스트(증강 Dickey-Fowler 테스트), 요약 통계(데이터의 여러 부분의 평균/분산 비교), 데이터 시각적 분석 등 데이터가 고정되어 있는지 테스트하는 다양한 방법이 있습니다. 모델링하기 전에 여러 테스트를 수행하는 것이 중요합니다.
ADF(Augmented Dickey-Fuller) 테스트는 시계열이 고정되어 있는지 확인하는 데 사용되는 '단위근 테스트'입니다. 기본적으로 귀무가설과 대립가설이 있고, 그 결과 나온 p-value를 바탕으로 결론을 내리는 통계적 유의성 검정이다.
귀무가설: 시계열 데이터가 정상적이지 않습니다.
대체 가설: 시계열 데이터는 고정되어 있습니다.
이 예에서 p-값이 0.05 이하이면 귀무 가설을 기각하고 데이터에 단위근이 없음을 확인할 수 있습니다.
from statsmodels.tsa.stattools import adfuller
result = adfuller(plant2_dcpower.values)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('t%s: %.3f' % (key, value))
ADF 테스트에서 p 값은 0.000553, < 0.05입니다. 이 통계를 바탕으로 데이터는 안정적인 것으로 간주될 수 있습니다. 그러나 그림 2(상단 그래프)를 보면 계절성의 명확한 징후가 있습니다(시계열 데이터가 고정된 것으로 간주되려면 계절성과 추세의 징후가 없어야 함). 이는 데이터가 비정상임을 나타냅니다. 따라서 여러 테스트를 실행하는 것이 중요합니다. < 0.05。根据这一统计数据,可以认为该数据是稳定的。然而,查看图2(最上面的图),有明显的季节性迹象(对于被认为是平稳的时间序列数据,不应该有季节性和趋势的迹象),这说明数据是非平稳的。因此,运行多个测试非常重要。
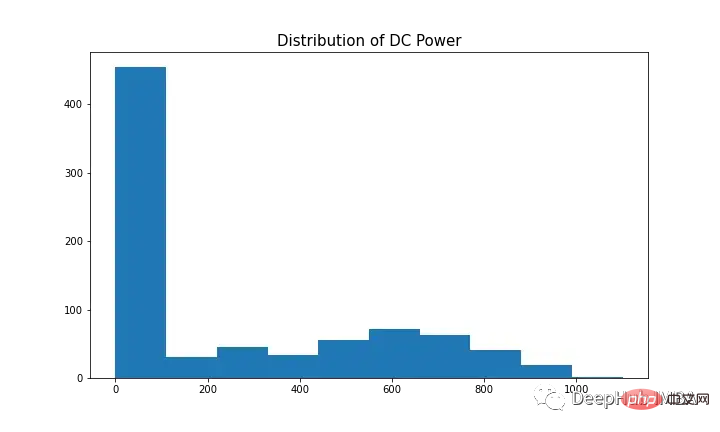
SARIMA를 사용하여 종속변수를 모델링하려면 시계열이 고정되어 있어야 합니다. 그림 9(첫 번째 및 세 번째 그래프)에 표시된 것처럼 DC에는 계절성의 뚜렷한 징후가 있습니다. 정규 분포와 유사해 보이기 때문에 그림 10에 표시된 것처럼 첫 번째 차이 [t-(t-1)]를 사용하여 계절 성분을 제거합니다. 이제 데이터는 고정되어 있으며 SARIMA 알고리즘에 적합합니다.
SARIMA의 하이퍼파라미터에는 p(자기회귀 순서), d(차이 순서), q(이동 평균 순서), p(계절 자기 회귀 순서), d(계절 차이 순서), q(계절 이동 평균 순서), m이 포함됩니다. (계절 주기의 시간 간격), 추세(결정적 추세).
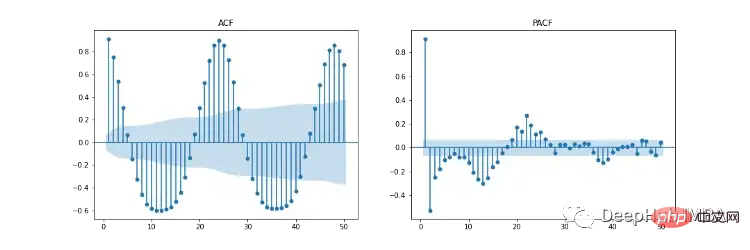
그림 11은 자기 상관(ACF), 부분 자기 상관(PACF) 및 계절별 ACF/PACF 도표를 보여줍니다. ACF 플롯은 시계열과 지연된 버전 간의 상관 관계를 보여줍니다. PACF는 시계열과 지연 버전 간의 직접적인 상관관계를 보여줍니다. 파란색 음영 영역은 신뢰 구간을 나타냅니다. SACF 및 SPACF는 원래 데이터에서 계절 차이(m)를 가져와 계산할 수 있습니다. 이 경우 ACF 플롯에는 24시간 계절 효과가 뚜렷하기 때문에 24입니다.
우리의 직관에 따르면 초매개변수의 시작점은 ACF 및 PACF 플롯에서 파생될 수 있습니다. 예를 들어 ACF와 PACF는 모두 점진적인 하향 추세를 보여줍니다. 즉, 자기회귀 차수(p)와 이동 평균 차수(q)가 모두 0보다 큽니다. p 및 p는 각각 PCF 및 SPCF 플롯을 살펴보고 시차 값이 중요하지 않게 되기 전에 통계적으로 유의미해지는 시차 수를 계산하여 결정할 수 있습니다. 마찬가지로 q와 q는 ACF 및 SACF 다이어그램에서 찾을 수 있습니다.
차이 차수(d)는 데이터를 고정시키는 차이의 수에 따라 결정될 수 있습니다. 계절 차이 차수(D)는 시계열에서 계절 성분을 제거하는 데 필요한 차이 수로부터 추정됩니다.
하이퍼파라미터 선택에 대한 이 기사를 읽을 수 있습니다: https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html
최소 평균 제곱 오차를 기반으로 하이퍼파라미터 최적화를 위해 그리드 검색 방법을 사용할 수도 있습니다. (MSE) ) p = 2, d = 0, q = 4, p = 2, d = 1, q = 6, m = 24, trend = 'n'(추세 없음)을 포함하는 최적의 하이퍼파라미터를 선택합니다.
from time import time
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.statespace.sarimax import SARIMAX
configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
print(f'SARIMA runtime: {round(time_len/60,2)} mins')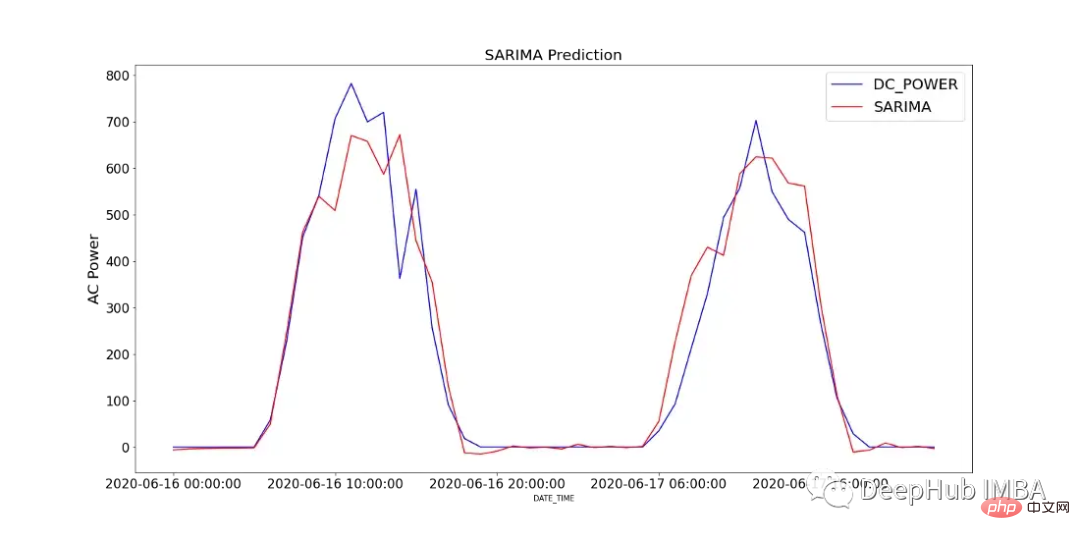
그림 12는 SP2에서 2일 동안 기록된 DC 전력과 SARIMA 모델의 예측값을 비교한 것입니다.
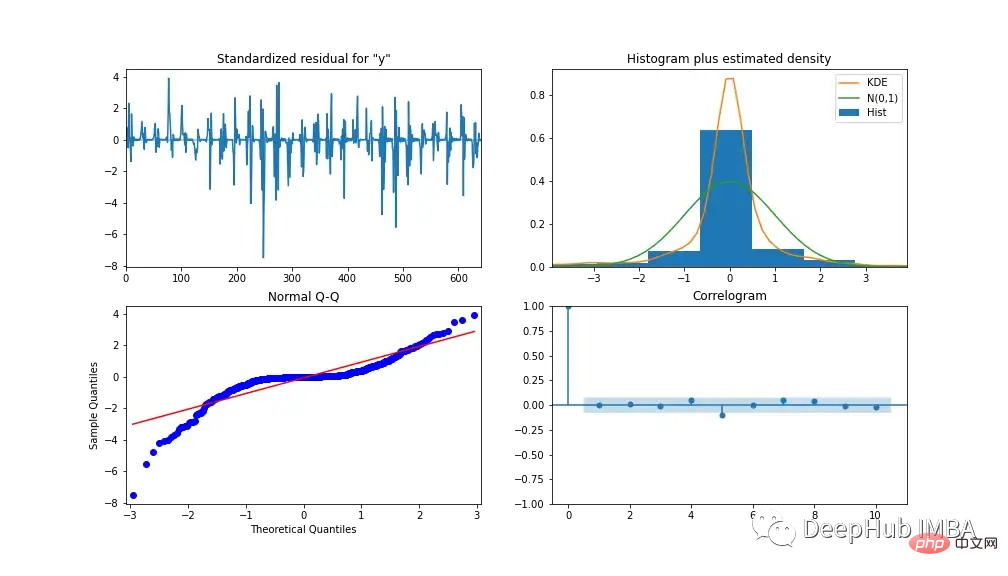
모델의 성능을 분석하기 위해 그림 13에 모델 진단이 나와 있습니다. 상관도는 첫 번째 시차 이후에는 상관관계가 거의 없음을 보여주며, 아래 히스토그램은 평균 0을 중심으로 정규 분포를 보여줍니다. 이를 통해 모델이 데이터에서 추가 정보를 수집할 수 없다고 말할 수 있습니다.
XGBoost(eXtreme Gradient Boosting)는 그라디언트 부스팅 결정 트리 알고리즘입니다. 기존 의사결정 트리 점수를 수정하기 위해 새로운 의사결정 트리 모델을 추가하는 앙상블 접근 방식을 사용합니다. SARIMA와 달리 XGBoost는 다변량 기계 학습 알고리즘입니다. 즉, 모델이 모델 성능을 향상시키기 위해 여러 기능을 채택할 수 있음을 의미합니다.
우리는 모델 정확도를 높이기 위해 특성 추출을 사용합니다. AC 및 DC 전력의 지연 버전인 S1_AC_POWER 및 S1_DC_POWER와 AC 전력을 DC 전력으로 나눈 전체 효율 EFF를 포함하는 3가지 추가 특성도 생성되었습니다. 그리고 데이터에서 AC_POWER 및 MODULE_TEMPERATURE를 제거합니다. 그림 14는 이득(특성을 사용한 분할의 평균 이득)과 가중치(특성이 트리에 나타나는 횟수)에 따른 특성 중요도 수준을 보여줍니다.

그리드 검색을 통해 모델링에 사용되는 하이퍼파라미터를 결정합니다. 결과는 다음과 같습니다. *학습률 = 0.01, 추정자 수 = 1200, 하위 표본 = 0.8, 트리별 colsample = 1, 수준별 colsample = 1, min child Weight = 20 및 최대 깊이 = 10
MinMaxScaler를 사용하여 훈련 데이터를 0과 1 사이로 조정합니다(데이터 분포에 따라 로그 변환 및 표준 스케일러와 같은 다른 스케일러를 사용해 실험할 수도 있습니다). 모든 독립 변수를 특정 시간만큼 뒤로 이동하여 데이터를 지도 학습 데이터 세트로 변환합니다.
import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn.preprocessing import MinMaxScaler
from time import time
def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
return result, test, xgb_model
if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
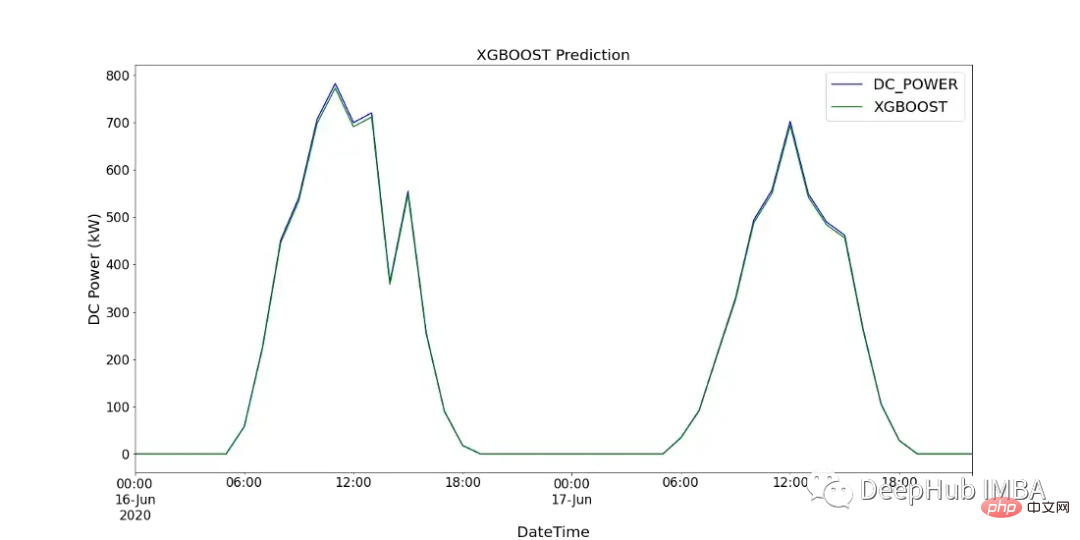
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。
CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络,在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型,旨在解决长期存在的梯度爆炸/消失问题,使用内部存储系统,允许它在输入序列上积累状态。
在本例中,使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入,所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似,使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放,但范围在-1到1之间。对于CNN-LSTM,需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features],以便可以将其作为输入传递给模型。
由于我们希望为每个子序列重用相同的CNN模型,因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。
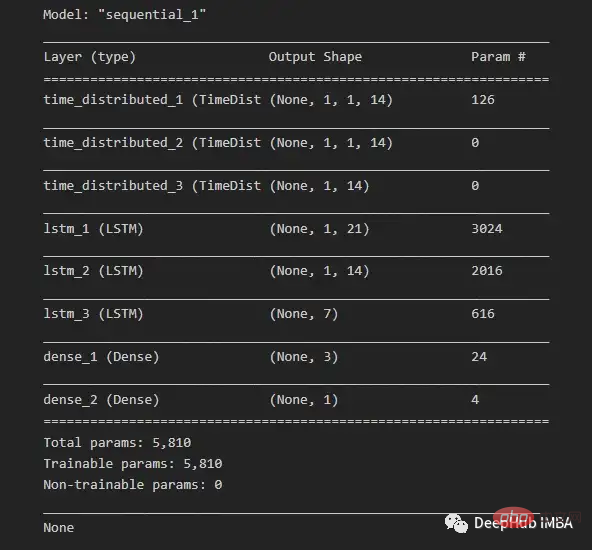
在将数据分解为训练数据和测试数据之后,将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后,模型可以进一步使用这一点来评估模型的性能。
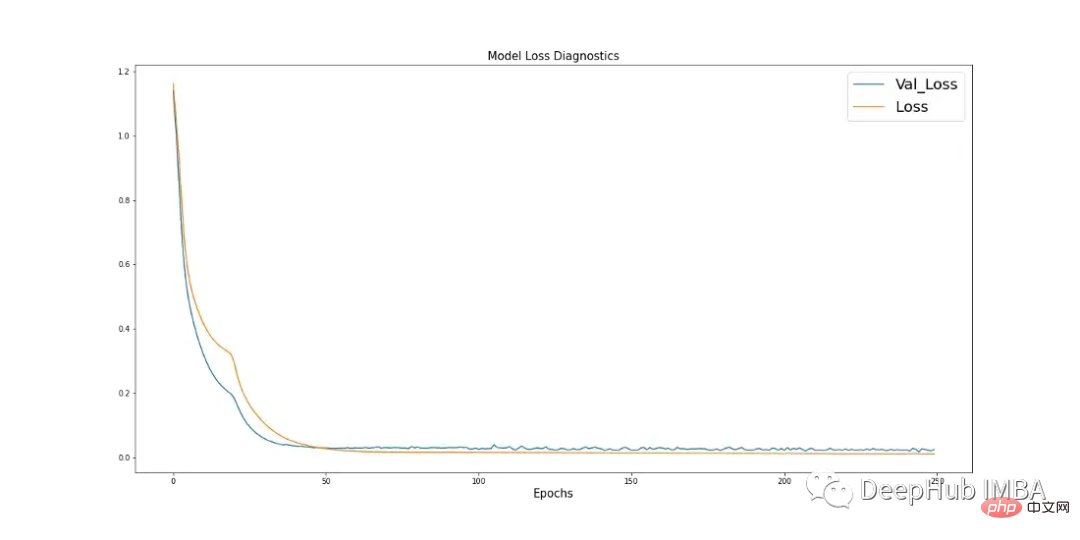
学习曲线是深度学习中使用的一个很好的诊断工具,它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习,并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
import keras
from keras.models import Sequential
from keras.layers.convolutional import Conv1D, MaxPooling1D
from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
from keras.optimizers import Adam
n_steps = 1
subseq = 1
def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
return np.array(x), np.array(y)
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
return model, history
# split and resahpe data
train, test = train_test_split(dropped_df_cat)
train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
#scale data
scaler_x = MinMaxScaler(feature_range=(-1,1))
scaler_y = MinMaxScaler(feature_range=(-1,1))
train_x = scaler_x.fit_transform(train_x)
train_y = scaler_y.fit_transform(train_y)
test_x = scaler_x.transform(test_x)
test_y = scaler_y.transform(test_y)
# shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
train_data_np = np.hstack((train_x, train_y))
x, y = split_data(train_data_np, n_steps)
x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
# create validation set
x_val, y_val = x_subseq[-24:], y[-24:]
x_train, y_train = x_subseq[:-24], y[:-24]
n_features = x.shape[2]
actual = scaler_y.inverse_transform(test_y)
# run CNN-LSTM model
if __name__ == '__main__':
start_time = time()
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
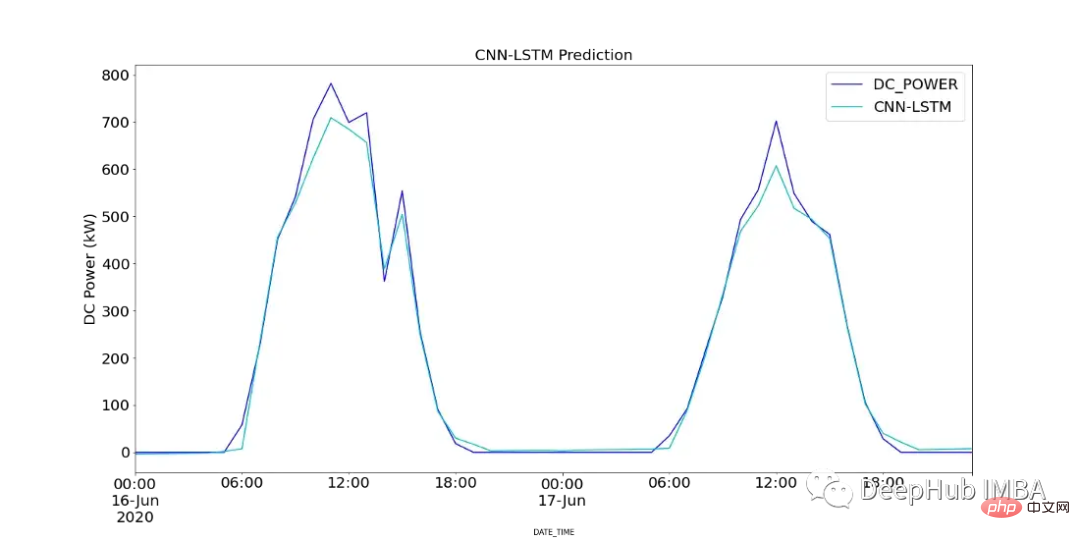
print(f"CNN-LSTM MSE: {round(mse,2)}")图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。
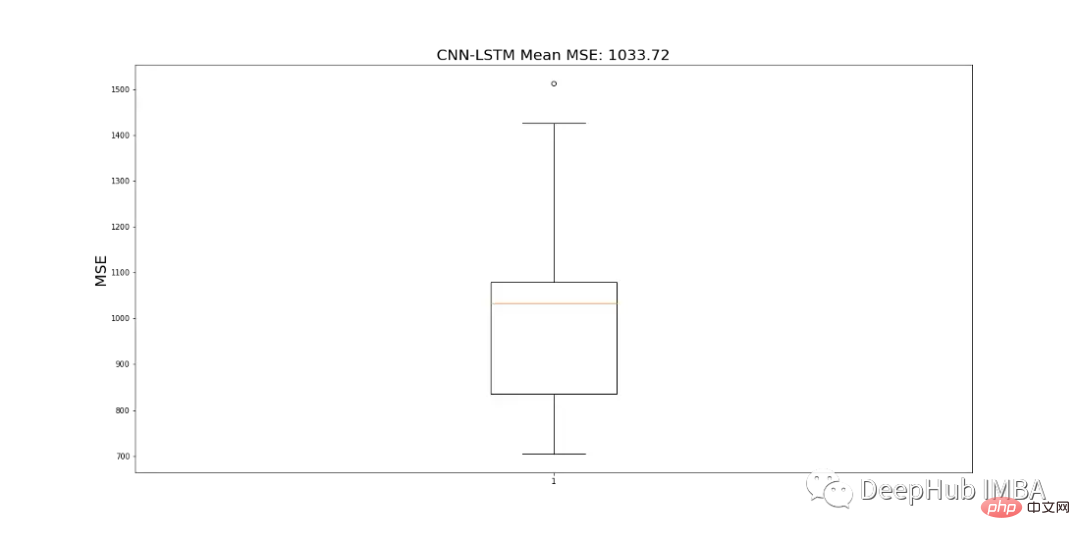
由于CNN-LSTM的随机性,该模型运行10次,并记录一个平均MSE值作为最终值,以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。
下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。
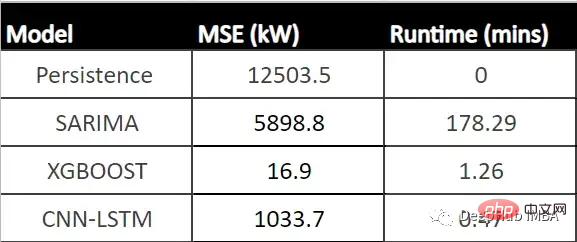
从表中可以看出,XGBoost的MSE最低、运行时第二快,并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时,它可以成为帮助运营经理决策过程的强大工具。
在本文中我们分析了SP1和SP2,确定SP1性能较低。所以对SP2的进一步调查显示,并且查看了SP2中那些模块性能可能有问题,并使用假设检验来计算每个模块在统计上明显表现不佳的次数,' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。
我们使用数据训练三个模型:SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差,XGBOOST表现最好,MSE为16.9,运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。
위 내용은 SARIMA, XGBoost 및 CNN-LSTM을 기반으로 한 시계열 예측 방법을 비교합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!