일반적인 차원 축소 기술 비교: 정보 무결성을 유지하면서 데이터 차원을 축소하는 타당성 분석

이 기사에서는 기계 학습 작업에서 표 형식 데이터에 대한 다양한 차원 축소 기술의 효과를 비교할 것입니다. 데이터 세트에 차원 축소 방법을 적용하고 회귀 및 분류 분석을 통해 효율성을 평가합니다. 다양한 도메인과 관련된 UCI에서 얻은 다양한 데이터 세트에 차원 축소 방법을 적용합니다. 총 15개의 데이터 세트가 선택되었으며, 그 중 7개는 회귀에 사용되고 8개는 분류에 사용됩니다.

이 기사를 쉽게 읽고 이해할 수 있도록 하나의 데이터 세트에 대한 전처리 및 분석만 표시됩니다. 실험은 데이터 세트를 로드하는 것으로 시작됩니다. 데이터 세트는 훈련 세트와 테스트 세트로 분할된 후 평균이 0, 표준 편차가 1이 되도록 정규화됩니다.

그런 다음 차원 축소 기술이 훈련 데이터에 적용되고 동일한 매개변수를 사용하여 차원 축소를 위해 테스트 세트가 변환됩니다. 회귀 분석에서는 차원 축소를 위해 PCA(주성분 분석)와 SVD(특이값 분해)를 사용하고, 차원 축소 후에는 선형 판별 분석(LDA)을 사용합니다. 테스트, 다양한 차원 축소 방법으로 얻은 다양한 데이터 세트에 대한 다양한 모델의 성능을 비교했습니다.

데이터 처리

import pandas as pd ## for data manipulation
df = pd.read_excel(r'RegressionAirQualityUCI.xlsx')
print(df.shape)
df.head()

데이터세트에는 15개의 열이 포함되어 있으며 그 중 하나는 레이블을 예측하는 데 필요합니다. 차원 축소를 계속하기 전에 날짜 및 시간 열도 제거됩니다.

X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1)
y = df['CO(GT)']
X.shape, y.shape

#Output: ((9357, 12), (9357,))

훈련을 위해서는 데이터 세트를 훈련 세트와 테스트 세트로 분할해야 차원 축소 방법과 차원 축소 특징 공간에서 훈련된 기계 학습 모델의 효율성을 평가할 수 있습니다. 모델은 훈련 세트를 사용하여 훈련되고 성능은 테스트 세트를 사용하여 평가됩니다.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape

#Output: ((7485, 12), (1872, 12), (7485,), (1872,))

데이터 세트에 차원 축소 기술을 사용하기 전에 입력 데이터의 크기를 조정하여 모든 기능이 동일한 크기에 있도록 할 수 있습니다. 일부 차원 축소 방법은 데이터가 정규화되었는지 여부에 따라 출력이 변경될 수 있고 특징의 크기에 민감하기 때문에 이는 선형 모델에 매우 중요합니다.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
X_train.shape, X_test.shape

주성분 분석(PCA)

선형 차원 축소의 PCA 방법은 데이터 분산을 최대한 유지하면서 데이터의 차원을 줄입니다.

여기에서는 Python sklearn.decomposition 모듈의 PCA 방법이 사용됩니다. 유지할 구성요소 수는 이 매개변수를 통해 지정되며 이 수는 더 작은 기능 공간에 포함되는 차원 수에 영향을 미칩니다. 대안으로, 캡처된 데이터의 분산량을 기반으로 구성 요소 수를 설정하는 목표 분산을 설정할 수 있습니다. 여기서는 0.95

from sklearn.decomposition import PCA
pca = PCA(n_compnotallow=0.95)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)
X_train_pca

위 기능이 무엇을 나타냅니까? PCA(구성 요소 분석)는 데이터를 저차원 공간에 투영하여 데이터의 차이를 최대한 보존하려고 노력합니다. 이는 특정 작업에 도움이 될 수 있지만 데이터를 이해하기 더 어렵게 만들 수도 있습니다. , PCA는 초기 특징의 선형 융합인 데이터에서 새로운 축을 식별할 수 있습니다.

특이값 분해(SVD)

SVD는 데이터 분산이 작은 특징을 저차원 공간에 투영하는 선형 차원 축소 기술입니다. 차원 축소 후에 유지할 구성 요소 수를 설정해야 합니다. 여기서는 차원을 2/3로 줄입니다.

from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33))
X_train_svd = svd.fit_transform(X_train)
X_test_svd = svd.transform(X_test)
X_train_svd

회귀 모델 학습

이제 위의 세 가지 유형의 데이터(원본 데이터 세트, PCA 및 SVD)를 사용하여 모델을 학습 및 테스트하고 비교를 위해 여러 모델을 사용합니다.

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.metrics import r2_score, mean_squared_error
import time

train_test_ML: 이 함수는 모델 훈련 및 테스트와 관련된 반복 작업을 완료합니다. 모든 모델의 성능은 rmse와 r2_score를 계산하여 평가되었습니다. 모든 세부 정보와 계산된 값이 포함된 데이터 세트를 반환합니다. 또한 각 모델이 해당 데이터 세트를 훈련하고 테스트하는 데 걸린 시간도 기록합니다.

def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken'])
for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
r2 = np.round(r2_score(y_test, y_pred), 2)
rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken]
return temp_df

원본 데이터:

original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test)
original_df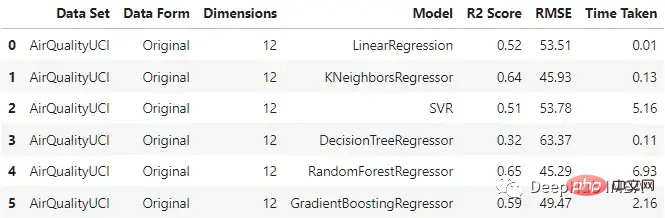

원본 데이터를 입력했을 때 KNN 회귀분석기와 랜덤 포레스트가 상대적으로 잘 수행되는 것을 볼 수 있으며, 랜덤 포레스트의 훈련 시간이 가장 길다는 것을 알 수 있습니다.

PCA

pca_df = train_test_ML('AirQualityUCI', 'PCA Reduced', X_train_pca, y_train, X_test_pca, y_test)
pca_df

与原始数据集相比，不同模型的性能有不同程度的下降。梯度增强回归和支持向量回归在两种情况下保持了一致性。这里一个主要的差异也是预期的是模型训练所花费的时间。与其他模型不同的是，SVR在这两种情况下花费的时间差不多。

SVD

svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test)
svd_df

与PCA相比，SVD以更大的比例降低了维度，随机森林和梯度增强回归器的表现相对优于其他模型。

回归模型分析

对于这个数据集，使用主成分分析时，数据维数从12维降至5维，使用奇异值分析时，数据降至3维。

• 就机器学习性能而言，数据集的原始形式相对更好。造成这种情况的一个潜在原因可能是，当我们使用这种技术降低维数时，在这个过程中会发生信息损失。
• 但是线性回归、支持向量回归和梯度增强回归在原始和PCA案例中的表现是一致的。
• 在我们通过SVD得到的数据上，所有模型的性能都下降了。
• 在降维情况下，由于特征变量的维数较低，模型所花费的时间减少了。

将类似的过程应用于其他六个数据集进行测试，得到以下结果:

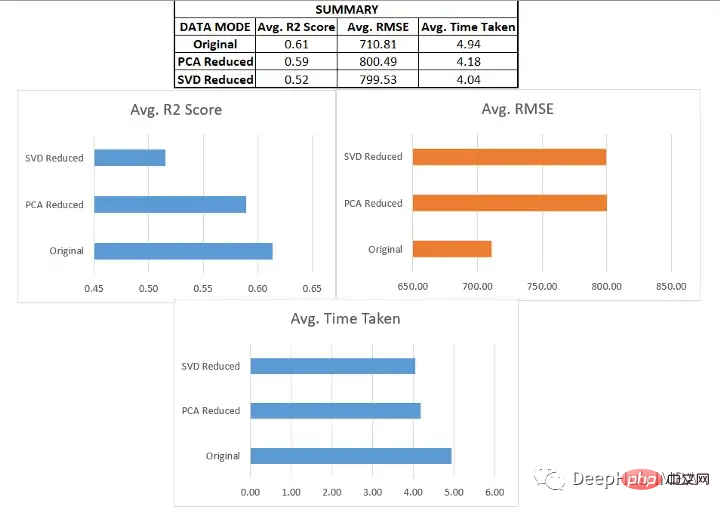
我们在各种数据集上使用了SVD和PCA，并对比了在原始高维特征空间上训练的回归模型与在约简特征空间上训练的模型的有效性

• 原始数据集始终优于由降维方法创建的低维数据。这说明在降维过程中可能丢失了一些信息。
• 当用于更大的数据集时，降维方法有助于显著减少数据集中的特征数量，从而提高机器学习模型的有效性。对于较小的数据集，改影响并不显著。
• 模型的性能在original和pca_reduced两种模式下保持一致。如果一个模型在原始数据集上表现得更好，那么它在PCA模式下也会表现得更好。同样，较差的模型也没有得到改进。
• 在SVD的情况下，模型的性能下降比较明显。这可能是n_components数量选择的问题，因为太小数量肯定会丢失数据。
• 决策树在SVD数据集时一直是非常差的，因为它本来就是一个弱学习器

训练分类模型

对于分类我们将使用另一种降维方法：LDA。机器学习和模式识别任务经常使用被称为线性判别分析(LDA)的降维方法。这种监督学习技术旨在最大化几个类或类别之间的距离，同时将数据投影到低维空间。由于它的作用是最大化类之间的差异，因此只能用于分类任务。

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score

继续我们的训练方法

def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken'])
for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
accuracy = np.round(accuracy_score(y_test, y_pred), 2)
f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2)
recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2)
precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken]
return temp_df

开始训练

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis()
X_train_lda = lda.fit_transform(X_train, y_train)
X_test_lda = lda.transform(X_test)

预处理、分割和数据集的缩放，都与回归部分相同。在对8个不同的数据集进行新联后我们得到了下面结果:

分类模型分析

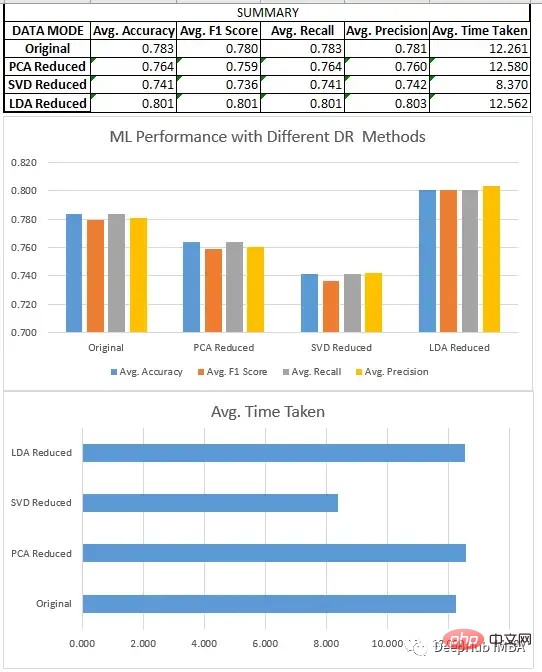
我们比较了上面所有的三种方法SVD、LDA和PCA。

• LDA数据集通常优于原始形式的数据和由其他降维方法创建的低维数据，因为它旨在识别最有效区分类的特征的线性组合，而原始数据和其他无监督降维技术不关心数据集的标签。
• 降维技术在应用于更大的数据集时，可以极大地减少了数据集中的特征数量，这提高了机器学习模型的效率。在较小的数据集上，影响不是特别明显。除了LDA（它在这些情况下也很有效），因为它们在一些情况下，如二元分类，可以将数据集的维度减少到只有一个。
• 当我们在寻找一定的性能时，LDA可以是分类问题的一个非常好的起点。
• SVD与回归一样，模型的性能下降很明显。需要调整n_components的选择。

总结

我们比较了一些降维技术的性能，如奇异值分解(SVD)、主成分分析(PCA)和线性判别分析(LDA)。我们的研究结果表明，方法的选择取决于特定的数据集和手头的任务。

회귀 작업의 경우 일반적으로 PCA가 SVD보다 더 나은 성능을 발휘하는 것으로 나타났습니다. 분류의 경우 LDA는 원본 데이터세트뿐만 아니라 SVD, PCA보다 성능이 뛰어납니다. 선형 판별 분석(LDA)이 분류 작업에서 주성분 분석(PCA)을 지속적으로 능가하는 것이 중요하지만 이것이 일반적으로 LDA가 더 나은 기술이라는 의미는 아닙니다. 이는 LDA가 데이터에서 가장 구별되는 특징을 찾기 위해 레이블이 지정된 데이터에 의존하는 지도 학습 알고리즘인 반면, PCA는 레이블이 지정된 데이터가 필요하지 않고 가능한 한 많은 분산을 유지하려고 하는 비지도 학습 알고리즘이기 때문입니다. 따라서 PCA는 감독되지 않은 작업이나 해석 가능성이 중요한 상황에 더 적합할 수 있는 반면 LDA는 레이블이 지정된 데이터와 관련된 작업에 더 적합할 수 있습니다.

차원 축소 기술은 데이터 세트의 기능 수를 줄이고 기계 학습 모델의 효율성을 높이는 데 도움이 될 수 있지만 모델 성능 및 결과 해석 가능성에 대한 잠재적 영향을 고려하는 것이 중요합니다.

이 문서의 전체 코드:

https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb

위 내용은 일반적인 차원 축소 기술 비교: 정보 무결성을 유지하면서 데이터 차원을 축소하는 타당성 분석의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!