업계 최초로 고체 시스템에 적합한 신경망 파동 함수가 Nature 저널에 게재되었습니다.

​머신 러닝은 방대한 양의 데이터를 처리하고, 복잡한 시나리오에서 과학적 문제를 해결하고, 이전에는 도달할 수 없었던 새로운 영역으로 과학적 탐구를 이끌 수 있습니다. 예를 들어 DeepMind는 인공 지능 소프트웨어 AlphaFold를 사용하여 과학계에 알려진 거의 모든 단백질 구조를 매우 정확하게 예측합니다. Christian Lagemann이 제안한 딥 러닝 기반 입자 이미지 속도 측정법(PIV)은 원래의 순수 수동 설정을 크게 개선했습니다. 모델의 적용 범위는 자동차, 항공우주, 생물의학공학 등 다양한 분야의 연구에 매우 중요합니다.

AlphaFold는 거의 모든 알려진 단백질의 구조를 예측할 수 있습니다. (출처: DeepMind)

해결해야 할 과학적 문제, 많은 기초 과학을 설명하기에 충분한 데이터와 정확한 모델이 있습니다." "한 세기 -오래된 미스터리'는 모두 머신러닝으로 해결될 수 있습니다. 유체역학, 응집물리학, 유기화학 등

최근 ByteDance AI Lab 연구팀과 베이징 대학교 물리학과 Chen Ji 연구 그룹의 "신경망 ansatz를 통한 실제 고체의 기본 계산" 작업은 응집 물질 물리학 연구에 새로운 아이디어를 제공했습니다. 제안된 작업은 업계 최초로 고체계에 적합한 신경망 파동함수를 개발하고, 고체의 제1원리 계산을 실현하고, 계산 결과를 열역학적 한계까지 끌어올렸습니다. 이는 신경망이 고체 물리학을 연구하는 데 효율적인 도구라는 점을 강력히 입증하고, 응집 물질 물리학에서 딥 러닝 기술이 점점 더 중요한 역할을 하게 될 것임을 나타냅니다. 관련 연구 결과는 국제 최고 학술지 네이처 커뮤니케이션(Nature Communication) 2022년 12월 22일자에 게재됐다.

논문 링크: https://www.nature.com/articles/s41467-022-35627-1

연구 배경 및 연구 방법

고체계에 대한 슈뢰딩거 방정식은 정확하게 해결 응집 물질 물리학의 성배 중 하나입니다. 지난 수십 년 동안 응집물질 연구에서는 밀도 함수 이론이 널리 채택되어 큰 성공을 거두었습니다.

밀도 함수 이론: 다중 전자 시스템의 전자 구조를 연구하는 양자 역학적 방법입니다.

이에도 불구하고 밀도 범함수 이론에는 여전히 많은 단점이 있습니다. 복잡하고 강력한 상관 시스템의 경우 밀도 범함수 이론은 정확도를 향상시키기 위한 체계적인 범함수 선택이 부족합니다. 최근에는 밀도함수론에 비해 보다 정확하고 보편적인 파동함수법이 점점 더 많은 관심과 연구를 받고 있다.

이러한 상황을 고려하여 북경대학교 물리학과 ByteDance AI Lab 연구팀과 Chen Ji 연구팀은 고체 시스템에 적합한 주기 신경망 파동 함수를 설계하고 이를 양자 몬테카를로 방법과 결합했습니다. 고체 시스템에 대한 첫 번째 원리 계산을 달성합니다. 이 연구에서는 처음으로 연속 공간의 고체 시스템 연구에 딥러닝 기술을 적용하여 계산을 열역학적 한계까지 끌어 올렸습니다.

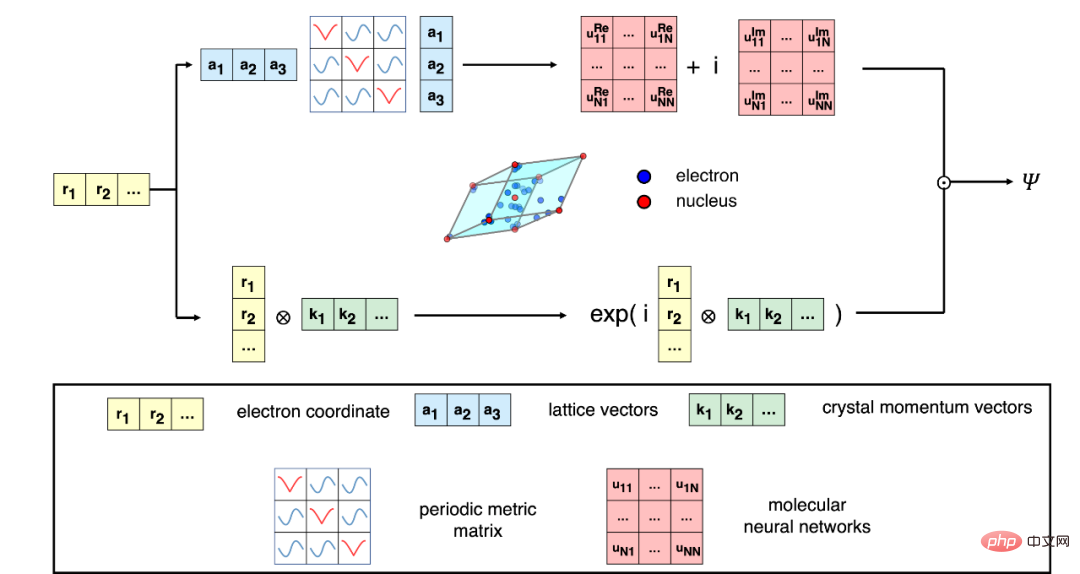
이 작업의 핵심은 주기적인 일반화 시스템 고유 벡터와 기존 분자 신경망 파동 함수를 결합하여 주기 대칭과 완전한 반대칭을 갖춘 견고한 시스템 파동 함수를 구성하는 것입니다. 그런 다음 연구에서는 양자 몬테카를로 방법을 적용하여 신경망을 효율적으로 훈련하고 다양한 실제 고체에서 테스트했습니다.

실험 결과 및 분석

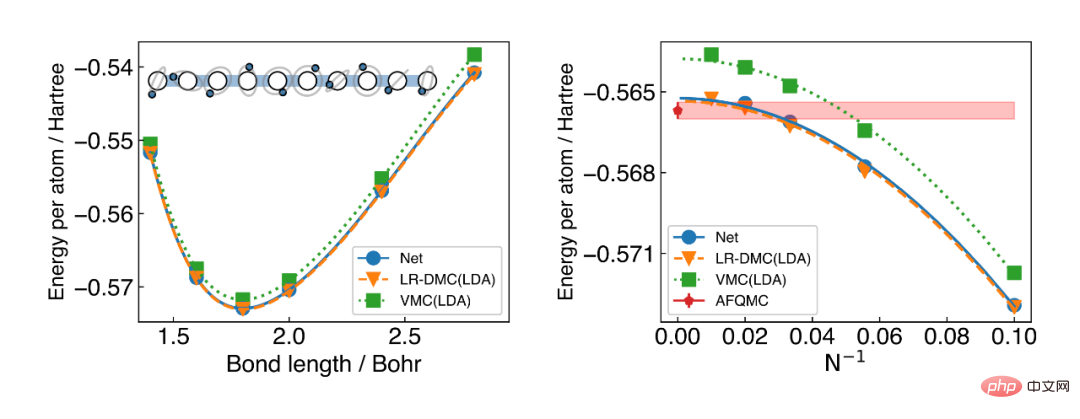
먼저 저자는 주기적인 1차원 수소 사슬에 대해 테스트했습니다. 1차원 수소 사슬은 응축 물질에서 가장 고전적인 시스템 중 하나이며, 정확한 해법은 사람들이 강하게 상관된 시스템의 특성을 이해하는 데 도움이 됩니다. 계산 결과는 신경망이 기존의 고정밀 방법(예: 보조 필드 Monte Carlo)과 유사한 정확도를 달성할 수 있음을 보여줍니다.

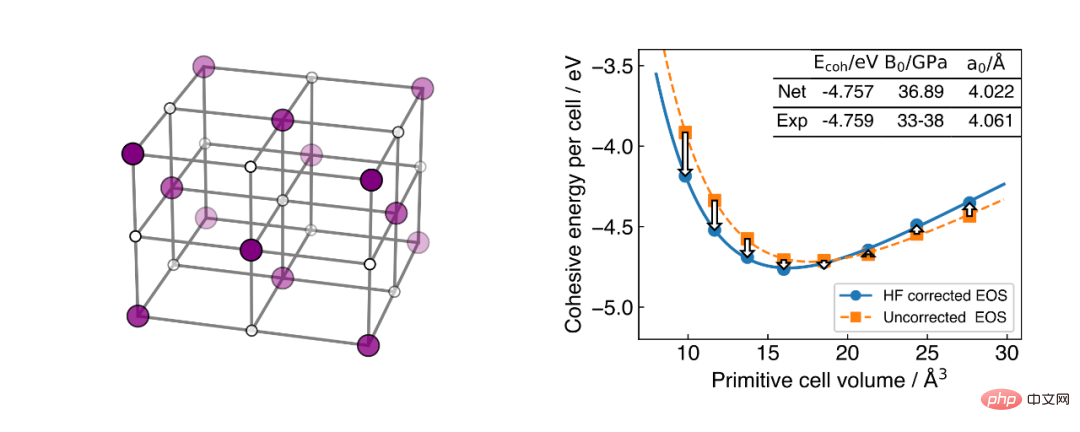
그런 다음 저자는 신경망을 사용하여 2차원 그래핀 물질을 계산했습니다. 그래핀은 지난 20년 동안 뜨거운 연구 소재였습니다. 열 전도성, 전기 전도성 및 기타 측면에서 그래핀의 독특한 특성은 중요한 연구 및 응용 가치를 가지고 있습니다. 이번 연구는 그래핀의 응집에너지를 정확하게 계산했으며, 계산 결과는 실험 데이터와 일치했다.

저자는 작업의 유효성을 더욱 검증하기 위해 3차원 리튬수소 소재를 계산하고 계산 규모를 열역학적 한계까지 밀어붙였습니다. 최대 계산 규모는 신경망이 사용하는 108전자에 달했습니다. 지금까지 시뮬레이션된 최대 솔리드 시스템이 가능했습니다. 계산된 응집 에너지와 재료의 벌크 계수는 실험 결과와 일치합니다.

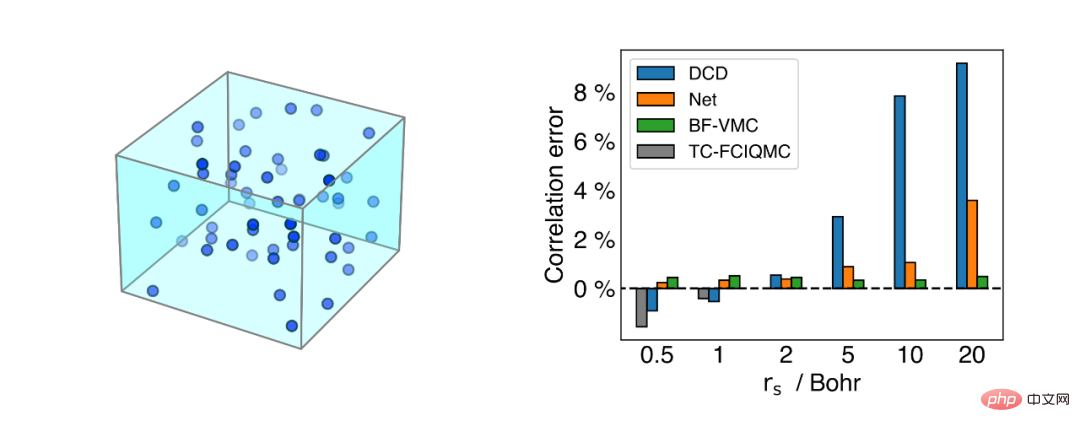
마지막으로 저자는 이론적으로 더 흥미로운 균일 전자 가스 시스템을 연구합니다. 균일한 전자 가스 시스템은 많은 새로운 물리적 효과(예: 양자 홀 효과)와 밀접하게 관련되어 있으므로 균일한 전자 가스에 대한 심층적인 이해는 중요한 이론적 가치를 갖습니다. 계산 결과는 신경망이 균일한 전자 가스에서 좋은 결과를 달성하여 많은 전통적인 고정밀 방법의 결과에 접근하거나 심지어 능가한다는 것을 보여줍니다.

이 작업은 신경망이 고체 물리학을 연구하는 데 효율적인 도구라는 것을 강력하게 입증합니다. 알고리즘이 더욱 개선됨에 따라 신경망 기술은 고체 시스템의 상 변화, 표면 물리학, 비전통적인 초전도체 등과 같은 응집 물질 물리학에서 더욱 중요한 역할을 할 것입니다. 이러한 주제에 대한 연구에는 초석으로서 고정밀 고체파 기능이 필요합니다. 동시에 저자는 응집물질 물리학 연구에 더 많은 가능성을 제공하기 위해 보다 효율적인 신경망 파동 함수 연구에도 노력하고 있습니다.

위 내용은 업계 최초로 고체 시스템에 적합한 신경망 파동 함수가 Nature 저널에 게재되었습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!