
안녕하세요 여러분 J형제입니다.
이것은 수학적 기초 없이는 계산하기 어렵습니다. 하지만 컴퓨터가 있을 때는 다릅니다. 컴퓨터의 매우 빠른 컴퓨팅 속도에 의존하여 미분이라는 개념을 사용하고 약간의 간단한 삼각법 지식을 추가하면 이를 달성할 수 있습니다.
자, 더 이상 고민하지 않고 알고리즘 원리를 살펴보겠습니다. 그림을 보세요:
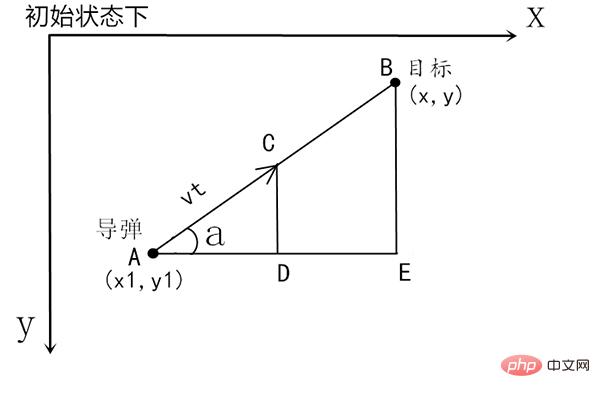
나중에 설명하기 위해 pygame을 사용할 것이므로 좌표계는 y축 아래쪽이므로 y도 사용합니다. 여기 하향 좌표계.
알고리즘의 일반적인 아이디어는 위 그림을 기반으로 시간 t를 충분히 작은 세그먼트(예: 1/1000, 시간 조각이 작을수록 더 정확함)로 나누는 것입니다. 위와 같이 미사일의 다음 시간 조각을 계산하면 걷는 방향(즉, ∠a)과 이동 거리(즉, vt=|AC|)가 계산되며, 이때 표적은 두 번째 시간 조각에서 다시 이동한 다음 방금 계산한 C 지점은 두 번째 시간 조각이 됩니다. 슬라이스의 초기 지점이 되고, 두 번째 시간 조각에서 C 지점과 새 목표 지점에 삼각형을 구성하여 새 vt를 계산하고, 세 번째 시간 조각을 입력하고 반복합니다.
미사일과 표적의 초기 좌표가 각각 (x1, y1), (x, y)라고 가정하고 직각삼각형 ABE를 구성합니다. 이 삼각형은 ∠의 사인 및 코사인 값을 찾는 데 사용됩니다. a, vt는 사용자가 직접 설정하므로 점 A의 x 및 y 좌표가 각각 얼마나 이동했는지 계산해야 합니다. 이동 값은 AD 및 CD의 길이에 vt cos(a)를 곱할 수 있습니다. ) 및 죄(a).
sin(a) 및 cos(a) 계산, 사인 대 기울기, 기울기에 인접한 코사인, 빗변은 두 점 거리 공식을 사용하여 계산할 수 있습니다. 즉:
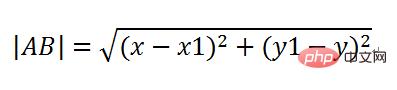
그런 다음
 의 길이
의 길이
AC는 미사일의 속도에 시간을 곱한 |AC|=vt이며 AD와 CD의 길이를 계산할 수 있습니다. 따라서 이 시간 조각이 지나면 미사일은 새로운 위치 C에 나타나야 합니다. , 그 좌표는 이전 지점 A입니다. x는 AD를 증가시키고 y는 CD를 뺀 값입니다.
그래서 점 C의 새로운 좌표는 다음과 같습니다.
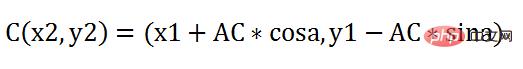
이 작업을 계속 반복해서 수행하세요. 음, 더 생생하게 만들기 위해 첫 번째 시간 조각과 두 번째 시간 조각을 합치겠습니다.
타임 슬라이스에 의해 생성된 첫 번째 삼각형은 ABE입니다. 타겟은 B 지점에서 D 지점으로 이동합니다. 이때 미사일은 C 지점에 있으므로 새로운 삼각형 CDF가 생성되고 계산 과정이 반복됩니다. of Ok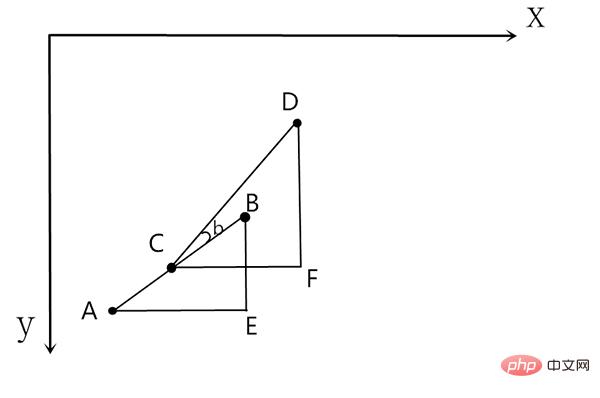 좋아, 나는 최근에 Python의 pygame 라이브러리를 사용하여 작은 게임을 만들었으므로 pygame을 사용하여 이 효과를 보여드리겠습니다.
좋아, 나는 최근에 Python의 pygame 라이브러리를 사용하여 작은 게임을 만들었으므로 pygame을 사용하여 이 효과를 보여드리겠습니다.
import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
old_angle=0
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置,鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点线段的弧度值
x1,y1=(x1+section*cosa,y1-section*sina)
d_angle = degrees(angle)#弧度转角度
screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
dis_angle=d_angle-old_angle#dis_angle就是到下一个位置需要改变的角度
old_angle=d_angle#更新初始角度
pygame.display.update()
 미사일을 입자로 간주한다면 위의 알고리즘으로 충분합니다. 왜냐하면 입자가 머리이든 꼬리이든 회전할 필요가 없기 때문입니다. 로드한 미사일 이미지가 아주 작을 때는 회전하지 않는 것으로 보입니다. 하지만 파이게임에서 회전하는 것은 쉬운 일이 아닙니다. 먼저 그림을 직사각형으로 바꾼 다음 회전 기능을 추가하여 효과를 살펴보겠습니다
미사일을 입자로 간주한다면 위의 알고리즘으로 충분합니다. 왜냐하면 입자가 머리이든 꼬리이든 회전할 필요가 없기 때문입니다. 로드한 미사일 이미지가 아주 작을 때는 회전하지 않는 것으로 보입니다. 하지만 파이게임에서 회전하는 것은 쉬운 일이 아닙니다. 먼저 그림을 직사각형으로 바꾼 다음 회전 기능을 추가하여 효과를 살펴보겠습니다missiled = pygame.transform.rotate(missile, -(d_angle)) screen.blit(missiled, (x1-missile.get_width(), y1- missile.get_height()/2))

大致方向相同,但是图片箭头的尖点并没有一直跟随鼠标,这是为什么呢。经过一番研究,我发现原来是这个图旋转的机制问题,我们看看旋转后的图片变成什么样了:
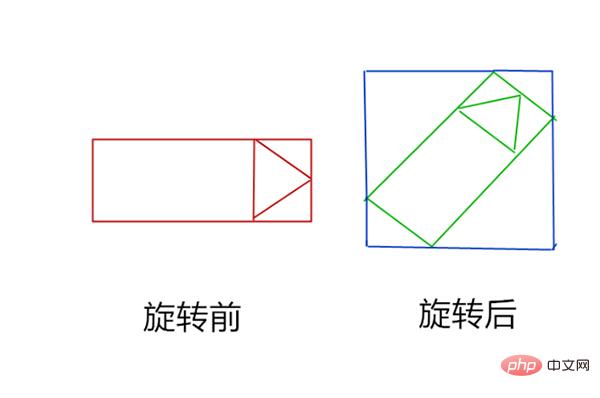
旋转后的图片变成了蓝色的那个范围,根据旋转角度的不同,所变成的图片大小也不一样,我们看旋转90的情况
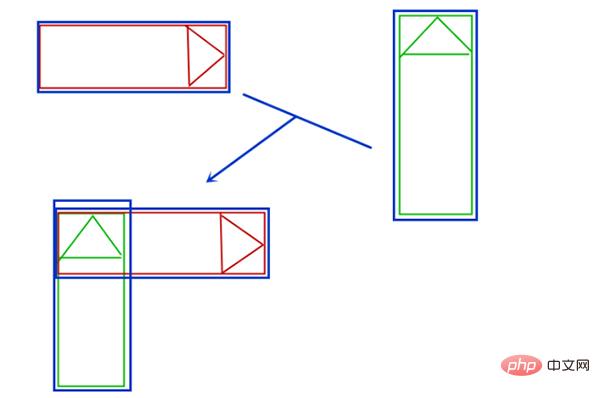
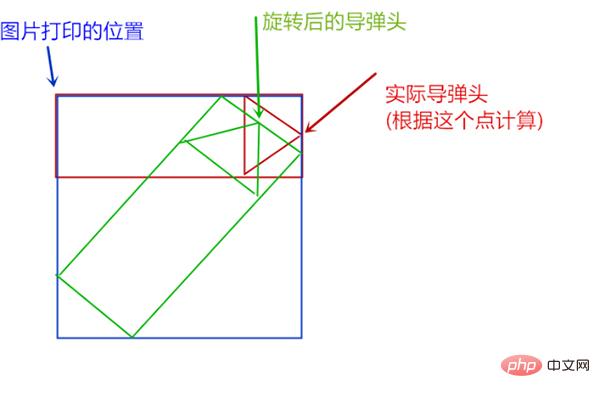
我们发现,旋转后的图片不仅面积变大了,导弹头的位置也变了。那应该怎么解决这个问题呢?思路是,每一次旋转图片以后,求出旋转图的头位置(图中的绿色箭头点),然后把绿图的打印位置移动一下,下,x,y分别移动两个头的距离,就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置,移动后应该是这样的:
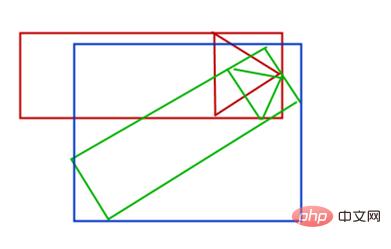
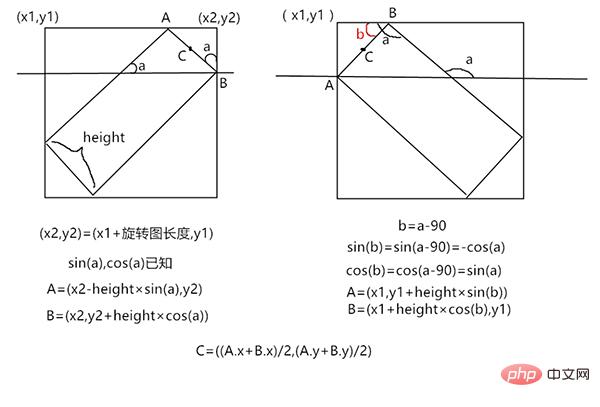
这样,两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同,旋转角在不同象限参数不一样,所以我们分为这四种情况
1,2象限
3,4象限,它的旋转只有正负0—180,所以3,4象限就是负角
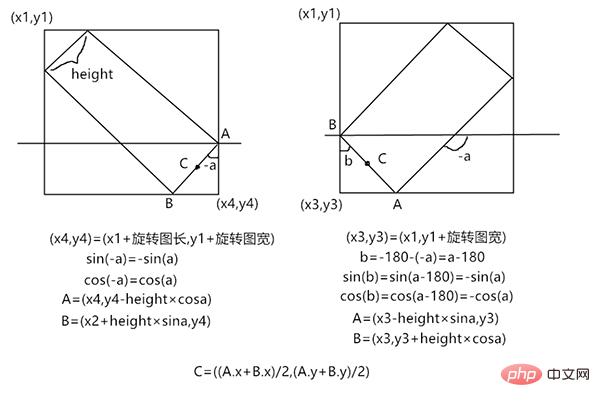
显示图片的时候我们将他移动
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)
所以最后我们加入相关算法代码,效果就比较完美了

大功告成,最后附上全部的算法代码
import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置,鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()
以上便是用Python模拟导弹自动追踪的代码实例。
위 내용은 Python을 사용하여 미사일 자동 추적, 슈퍼 연소 구현!의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!