그래프 컴퓨팅에 대해 배우고 생각하기-일체 포함-php.cn

좋은 소프트웨어는 프로그램 분석이나 오류 검사를 통해 발견되는 것이 아니라 올바른 사람이 만드는 것입니다.

그래프는 점점 더 중요한 컴퓨팅 개체가 되었습니다. 그래프 구조는 그룹 관계의 추상화이며 풍부한 개체와 관계를 설명할 수 있습니다. 그래프 컴퓨팅의 핵심은 데이터를 그래프 구조로 모델링하는 방법과 문제의 해를 그래프 구조에서 컴퓨팅 문제로 변환하는 방법입니다. 문제에 상관 분석이 포함된 경우 그래프 컴퓨팅이 자연스럽게 문제에 대한 솔루션을 만들 수 있는 경우가 많습니다. 그래프 구조에 대한 일련의 연산과 계산으로 표현됩니다. 예를 들어, 웹 페이지 링크의 그래프 구조를 기반으로 하는 페이지랭크(PageRank) 알고리즘은 웹 페이지의 가중치를 구하는 데 사용되며, 이는 검색 엔진 순위의 기준으로 사용됩니다. 그래프 구조의 사용자 행동 데이터는 정확한 값을 구하는 데 사용됩니다. 집단 선호도 분석 및 개인화된 상품 추천 결과를 제공합니다.

1. 그래프 컴퓨팅이란?

그래프 컴퓨팅은 인간 세상의 사물과 사물 간의 관계를 연구하고, 이를 기술하고, 특성화하고, 분석하고, 계산하는 기술입니다. 여기서 그래프는 수학의 그래프 이론에서 유래한 그래프 '이미지'가 아닌 '그래프'입니다.

그래프는 엔터티를 제한 없이 연결할 수 있는 가장 유연한 연결 방법입니다. 그래프 컴퓨팅은 단순한 기술이 아니라 세상을 이해하는 방법입니다. 그래프 데이터는 연결의 방향과 속성을 설명하는 것을 포함하여 사물 간의 연결을 잘 설명할 수 있습니다. 데이터 구조의 관점에서 볼 때 그래프는 사물 간의 관계를 기본적으로 표현하는 것입니다. 어느 정도 관계형 데이터베이스는 테이블 데이터베이스라고 불러야 하고, 그래프 데이터베이스는 관계형 데이터베이스라고 불러야 합니다. 광범위하게 정의된 그래프 컴퓨팅이란 그래프 데이터베이스를 포함해 그래프 데이터를 기반으로 한 다양한 처리를 의미합니다.

그래프 컴퓨팅 기술은 기존 컴퓨팅 모드에서 관련 쿼리의 효율성이 낮고 비용이 많이 드는 문제를 해결하며 문제 영역의 관계를 완벽하게 묘사하며 풍부하고 효율적이며 민첩한 데이터 분석 기능을 갖추고 있습니다.

그래프 추상화 기반 데이터 모델
그래프 데이터 모델 병렬 추상화
그래프 모델 시스템 최적화

그래프 컴퓨팅에서는 성능 비용, 내결함성 메커니즘 및 확장성이 모두 매우 중요합니다.

2. 역사적 발전의 관점에서 그래프 컴퓨팅을 살펴보기

그래프 컴퓨팅은 1960년대와 1980년대에 LDM과 같은 트리 구조의 데이터베이스로 거슬러 올라갑니다. 논리적 데이터 모델) 등. 2007년까지 최초의 상용 그래프 데이터베이스 Neo4j가 구축되면서 그래프 컴퓨팅이 개발 단계에 진입했습니다.

그래프 컴퓨팅 연구의 진정한 시작은 2004년 Google이 빅 데이터 병렬 처리를 위한 컴퓨팅 모델인 MapReduce를 개발한 것입니다. 이 모델의 출시는 빅 데이터 병렬 처리에 엄청난 혁명적인 영향을 미쳤습니다. 이후 2006년에 Apache Hadoop 팀은 HDFS(Hadoop 분산 파일 시스템)와 새로운 Hadoop MapReduce 프레임워크를 도입했습니다. 2009년 캘리포니아 대학교 버클리 캠퍼스의 AMP 연구소는 스파크 시스템을 개발했습니다.

2010년부터 대규모 분산 아키텍처, 멀티모달 지원, 그래프 쿼리 언어 설계 등 그래프 컴퓨팅 연구 방향이 점차 주목을 받고 있습니다. Google은 BSP 컴퓨팅 모델을 따라 그래프 알고리즘의 특성에 맞게 설계된 분산 그래프 컴퓨팅 시스템인 Pregel을 제안했으며, 이후 CMU Select Laboratory GraphLab 프로젝트 팀은 GAS 컴퓨팅 모델을 제안했습니다. . pregel과 GraphLab은 모두 복잡한 기계 학습 계산을 위한 처리 프레임워크이고 반복 계산에 사용되지만 구현 방법은 서로 다릅니다. Pregel은 대형 블록 메시지 전달 메커니즘을 기반으로 하고 GraphLab은 메모리 공유 메커니즘을 기반으로 합니다. 다른 그래프 컴퓨팅 시스템의 후속 설계에 큰 영향을 미칩니다.

Google은 2012년 5월 정보를 연결하는 새로운 방식인 지식 그래프 개념을 제안했습니다. 기본 단위는 "엔티티-관계-엔티티"이며, 엔터티는 관계를 통해 서로 연결되어 네트워크화된 지식을 구성합니다. 구조. 지식 그래프 구축의 핵심은 컴퓨터의 지식 추론 메커니즘이며, 그래프 컴퓨팅은 이에 대한 중요한 기반 기술 지원을 제공합니다.

2015년에는 데이터 양의 급격한 증가와 함께 애플리케이션 시장이 점차 개방되었으며, 그래프 컴퓨팅 시스템의 확장성과 효율성에 대한 수요가 지속적으로 증가했습니다. 중국의 그래프 컴퓨팅 분야의 학술 및 산업 연구는 Tsinghua University의 Gemini 등과 같은 자체 그래프 컴퓨팅 시스템 및 플랫폼을 점차적으로 개발하기 시작했습니다.

최근에는 인공지능 기술이 발전하면서 그래프 신경망도 업계에서 그 위력을 발휘하고 있습니다.

3. 프레임워크 모델에서 그래프 컴퓨팅을 살펴보기

그래프 컴퓨팅의 프레임워크는 기본적으로 BSP(Bulk 동기 병렬) 컴퓨팅 모델을 따릅니다. BSP 모드 벌크 동기화 메커니즘의 독특한 특징은 슈퍼스텝 개념의 도입에 있습니다. 계산 프로세스는 일련의 글로벌 수퍼스텝으로 구성됩니다. 각 수퍼스텝은 병렬 계산(로컬 계산), 글로벌 통신(비로컬 데이터 통신), 펜스 동기화(통신 동작 종료 대기)의 세 단계로 구성됩니다.

BSP 모드에는 다음과 같은 특징이 있습니다.

계산을 하나씩 수퍼스텝으로 나누어 교착 상태를 효과적으로 방지합니다.

프로세서와 라우터를 분리하여 컴퓨팅 작업과 통신 작업의 분리를 강조하고 라우터는 지점 간 메시징만 완료합니다. 특정 상호 연결 네트워크 토폴로지를 마스킹할 뿐만 아니라 통신 프로토콜을 단순화하는 조립, 복사 및 방송과 같은 기능을 제공하지 않습니다.

동기식 모드를 채택하여 하드웨어에서 전역 동기화 및 제어 가능한 대략적인 수준을 구현하여 긴밀하게 결합된 동기식 병렬 알고리즘을 실행합니다.

그래프 컴퓨팅에 대해 배우고 생각하기

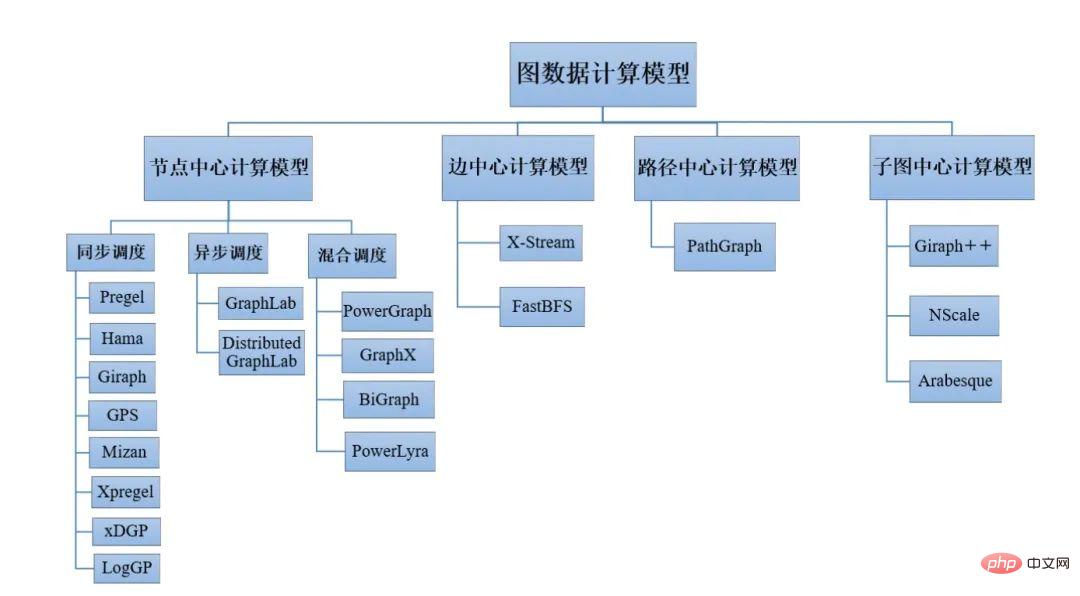
대표적인 그래프 컴퓨팅 프레임워크는 다음과 같습니다.

Neo4j-APOC: 그래프 데이터베이스를 기반으로 몇 가지 기본적인 그래프 알고리즘을 지원하며, 분산 버전은 오픈 소스가 아닙니다.
프레겔(Pregel): 2009년 구글이 제안한 그래프 컴퓨팅 모델의 창시자이며, 이후 많은 작품이 그 아이디어에 영향을 받았습니다. 오픈 소스가 아닙니다.
Giraph: Pregel의 아이디어를 기반으로 한 Facebook의 오픈 소스 구현입니다.
Gemini: Tsinghua University는 Pregel 아이디어를 기반으로 뛰어난 성능으로 여러 가지 개선 사항을 구현했습니다. 무료 데모만 제공되며, 상용 버전은 오픈소스가 아닙니다.
KnightKing: 워커 걷기 알고리즘을 위해 특별히 설계된 그래프 컴퓨팅 프레임워크로, 보편적이지 않습니다.
GraphX: Apache Foundation에서 Spark 기반으로 구현한 그래프 컴퓨팅 프레임워크로, 커뮤니티 활동이 높습니다.
GraphLab(PowerGraph): 오픈 소스가 아닌 상용 소프트웨어입니다. Apple에 인수되었습니다.
Plato: Gemini와 KnightKing의 아이디어를 기반으로 한 Tencent의 C++ 오픈 소스 구현은 확장 가능하고 연결하기 쉬운 고성능 그래프 컴퓨팅 프레임워크입니다.

4. 알고리즘 관점에서 그래프 계산을 살펴보기

그래프 알고리즘은 특정 정점과 모서리를 사용하여 답을 찾는 간단한 방법을 의미하며 일반적으로 사용되는 많은 그래프 알고리즘을 무방향 그래프, 유방향 그래프 및 네트워크에 사용할 수 있습니다. 그래프 데이터의 경우 순회 알고리즘(깊이/너비 우선)이 다른 알고리즘의 기초입니다. 일반적인 그래프 알고리즘에는 PageRank, 최단 경로, 연결된 분기, 최대 독립 집합, 최소 스패닝 트리 및 Bayesian Belief Propagation이 포함됩니다. 그래프의 최소 스패닝 트리는 인생에서 가장 낮은 비용 또는 최소 비용을 나타내는 경우가 많으며 일반적으로 Prim의 알고리즘과 Kruskal의 알고리즘이 사용됩니다. 커뮤니티 검색, 최단 경로, 위상 정렬 및 중요 경로에도 해당 알고리즘이 있습니다.

그래프 알고리즘에는 검색, 매칭, 분류, 평가 등 다양한 데이터 분석 기술이 포함되어 있으며, 알고리즘 구조 차원에서 크게 순회 중심 알고리즘과 계산 중심 알고리즘으로 나눌 수 있습니다. 순회 중심 알고리즘은 특정 정점에서 특정 방식으로 그래프를 순회해야 하며, 무작위 액세스가 많습니다. 계산 중심 알고리즘은 반복 주기에 많은 연산이 필요하며 상대적으로 데이터 지역성이 좋습니다.

그래프 컴퓨팅에 대해 배우고 생각하기

5. 그래프 컴퓨팅을 컴퓨터 아키텍처의 관점에서 바라보기

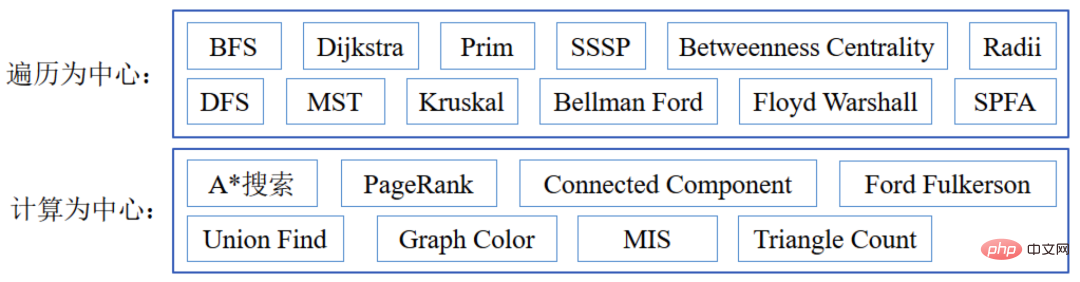
그래프 컴퓨팅은 일반적으로 데이터 기반 계산이므로 실행하기 전에는 컴퓨팅 구조를 정확하게 예측할 수 없으며 형식에 있어서도 명확한 패턴이 없습니다. 효율적이고 고품질로 나누기가 어렵습니다. 기존 캐싱 메커니즘은 지역성이 좋은 경우에만 데이터 액세스 속도를 높일 수 있습니다. 대량의 데이터에 액세스하면 프로세서가 I/O를 기다리는 상태가 되는 경우가 많습니다.

그래프 컴퓨팅 부하는 복잡하며, 가장 대표적인 그래프 컴퓨팅 부하는 없습니다. 정점을 연결하는 가장자리는 수많은 가능한 연결 중 작은 부분 집합일 뿐이며 매우 불규칙합니다. 그래프 컴퓨팅 과정에서 읽기와 쓰기의 시공간적 위치를 파악하기 어렵고 대역폭 점유도 예측하기 어렵습니다.

대부분의 알고리즘은 메모리 대역폭의 50% 미만을 차지할 수 있습니다. 메모리 대역폭 활용을 제한하는 것은 무엇입니까? 프로세서는 명령어를 얻어야 하고 명령어 창 사이에 공간이 있어야 하며 레지스터 피연산자는 피연산자를 사용할 수 있을 때까지 기다려야 하며 관련 종속성은 해제되지 않습니다. 높은 명령어 적중률로 인해 메모리 수준의 병렬성이 감소하여 플랫폼의 메모리 대역폭을 완전히 활용하기 어려울 수 있습니다. 캐시 데이터 사용 비율이 낮다는 것은 애플리케이션이 공간적 지역성의 이점을 얻기 어렵고 데이터 프리페치 전략이 효과적이지 않다는 것을 의미합니다. 데이터 프리페치는 일반적으로 성능 향상에 도움이 되지만 쓸모 없는 프리페치 작업도 많이 생성됩니다. 메모리 대역폭이나 캐시 용량이 제한된 애플리케이션의 경우 데이터 프리페칭으로 인해 리소스가 낭비될 수 있습니다. 멀티스레드 컴퓨팅의 경우 대기 시간이 더 긴 원격 메모리 액세스를 트리거하면 멀티스레딩의 이점도 상쇄됩니다.

그래프 컴퓨팅에는 어떤 종류의 프로세서 코어가 필요합니까? 일반적으로 작은 컴퓨팅 코어가 많고 스레드 수가 많은 아키텍처가 사용되는데, 이는 기존 멀티 코어 프로세서가 잘 수행하지 못하는 대규모 그래프 계산을 처리하는 데 적합합니다. 여러 그래프의 동시 계산에는 공유 할당과 배타적 할당이라는 두 가지 전략이 있습니다. 공유 할당 전략은 m개의 요청 각각이 n개의 논리 코어를 사용하여 병렬로 처리되고 OS가 논리 코어에서 서로 다른 요청의 전환을 관리하는 것을 의미합니다. 배타적 할당 전략은 논리적 코어가 작업 간에 전환될 필요가 없도록 각 요청에 n/m개의 논리적 코어를 할당하는 것을 의미합니다. 단독 할당 전략은 동시 그래프 계산에 더 적합합니다. 일반적으로 단독은 동일한 동시 요청에 대한 전체 실행 시간을 줄일 수 있습니다. 재정렬 캐시의 낮은 경합은 동시 그래프 컴퓨팅 시나리오에서 배타적 전략이 공유 전략보다 나은 이유일 수 있습니다.

그래프 계산으로 인한 전력 소비의 경우, 부하 변화로 인해 시스템 전력 변동이 발생하고 최고점과 최저점은 엇갈릴 수 있습니다. 동시 작업이 증가하면 최고 대 최저 비율이 변경되고 전력 소비가 증가합니다. 일반적으로 CPU 전력 소비 측면에서 계산 중심 알고리즘은 평균적으로 명령어당 많은 양의 에너지를 소비하는 반면, 순회 중심 알고리즘은 메모리 전력 소비 측면에서 반대 효과를 가지며 계산 중심 알고리즘은 메모리를 덜 소비합니다. 평균 에너지 소비는 적으며 순회 중심 알고리즘의 경우 그 반대입니다.

대부분의 그래프 컴퓨팅 기반 응용 프로그램은 메모리가 제한되어 있지만 핵심 구성 요소의 제한으로 인해 메모리 활용도가 부족합니다. 활성 스레드가 충분하면 동시 액세스가 생성되어 활용도가 향상될 수 있습니다. 더 많은 스레드가 필요하지만 스레드 간의 불균형으로 인해 효율적으로 사용되지 않을 수 있습니다. 멀티 코어 프로세서의 고대역폭 메모리 사용을 최적화하려면 더 확장 가능한 병렬 전략을 제공해야 합니다. 전력 소비와 에너지 소비 동작은 지시 관점과 정점 계산 관점에서 다르기 때문에 정확한 전력 관리 방법이 필요하며 광범위한 조정은 효과적이지 않을 수 있습니다.

6. 시스템에서 그래프 컴퓨팅 보기

대규모 그래프 컴퓨팅 시스템의 사용 시나리오 및 컴퓨팅 플랫폼 아키텍처를 기반으로 단일 머신 메모리 그래프 컴퓨팅 시스템, 단일 머신 외부 메모리 그래프 컴퓨팅 시스템으로 나눌 수 있습니다. , 분산 메모리 그래프 컴퓨팅 시스템 및 분산 메모리 그래프 컴퓨팅 시스템.

그래프 컴퓨팅에 대해 배우고 생각하기

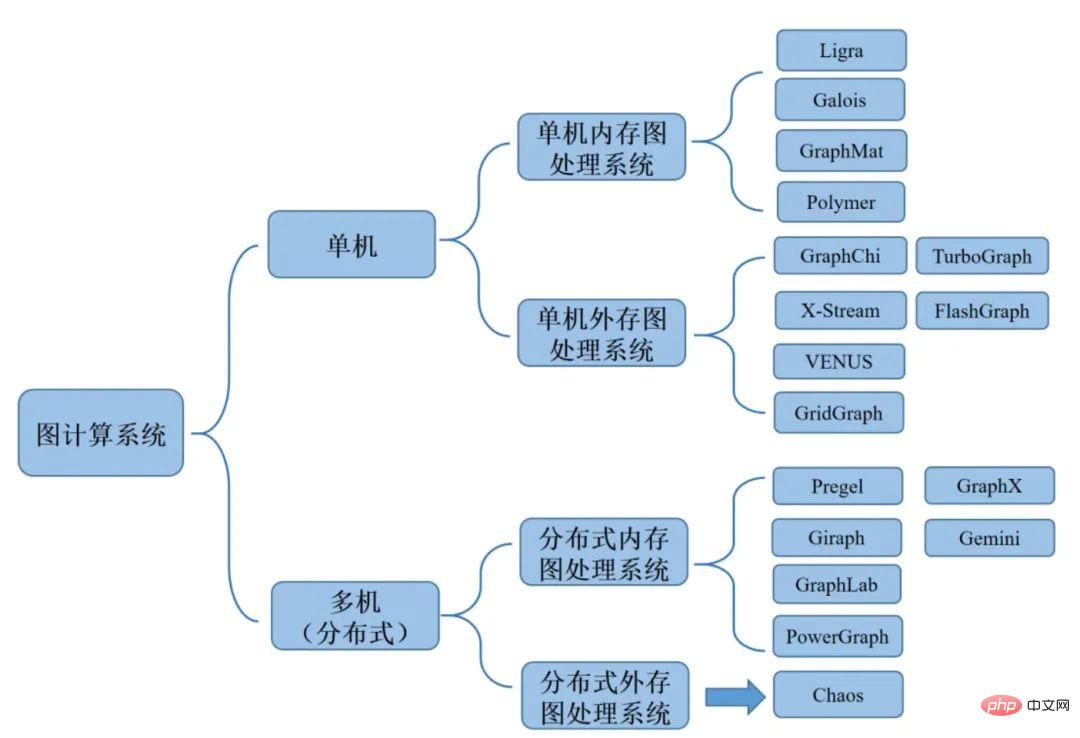
단일 머신 메모리 그래프 처리 시스템은 단일 머신 환경에서 실행되고 모든 그래프 데이터를 메모리에 버퍼링하는 그래프 처리 시스템입니다. 독립형 외부 메모리 그래프 처리 시스템은 그래프 처리 시스템이 독립형 환경에서 실행되며 그래프 데이터 계산을 통해 메모리 및 디스크와 지속적으로 상호 작용하는 효율적인 그래프 알고리즘입니다. 분산 메모리 시스템은 분산 클러스터 환경에서 실행되는 그래프 처리 시스템으로, 모든 그래프 데이터가 메모리에 로드됩니다. 분산 외부 메모리 그래프 컴퓨팅 시스템은 단일 머신 외부 시스템을 클러스터로 확장하고 수조 단위의 에지가 있는 그래프를 처리할 수 있습니다.

7. AI에서 그래프 컴퓨팅을 바라보다

AI와 그래프 컴퓨팅의 융합으로 생성된 그래프 신경망(GNN)은 현재 빠르게 발전하고 있는 중요한 분야입니다. 다양한 엔터티 간의 관계 데이터를 신경망과 결합하는 방법은 무엇입니까? 그래프 신경망은 표현 학습을 사용합니다. 그래프의 구조를 통해 각 노드 또는 가장자리를 먼저 벡터로 표현한 다음 신경망을 사용하여 추가 처리합니다. 이는 신경망 사용 범위를 확장하고 엔터티 간의 관계를 AI 처리에 도입합니다.

그래프 신경망은 노드의 대표 특징이나 그래프 레벨의 대표 특징 등 그래프 특징을 학습하는 과정으로 볼 수 있습니다. 일반적으로 그래프의 속성과 그래프의 구조를 입력으로 받아 집합을 출력합니다. 업데이트된 노드 표현. 일반적으로 이 프로세스를 그래프 필터링 작업이라고도 합니다. 그래프 필터링은 노드 기능을 업데이트하지만 그래프의 구조를 변경하지는 않습니다. 그래프 신경망의 개발은 다양한 이론적 동기에서 개발되었습니다. 예를 들어, GNN이 비유클리드 거리의 컨볼루션 일반화로 간주된다면 현재 대부분의 GNN은 신경 메시지 전달 방법을 기반으로 합니다. 그래픽 모델의 확률적 추론에 대한 유추를 통해 제안된 통과 알고리즘.

스펙트럼 방법이든 공간 기반 아이디어이든 그래프 신경망은 마침내 메시지 전달을 기반으로 하는 프레임워크로 통합될 수 있습니다. GNN 메시지 전달 프레임워크의 기본 아이디어는 각 반복에서 각 노드가 이웃 노드의 정보를 집계한다는 것입니다. 반복 횟수가 증가할수록 각 노드에는 그래프에 더 넓은 범위의 정보가 포함됩니다. 예를 들어, k번 반복 후에 중앙 노드는 k-홉 이웃에 대한 정보를 얻을 수 있습니다. 핵심 아이디어는 그래프 구조와 알려진 특징 정보를 기반으로 노드 표현을 생성하는 것입니다. GNN은 그래프의 구조 및 노드 특징 정보를 사용하여 심층 임베딩 표현을 생성하는 반면, 기존 그래프 임베딩 방법은 그래프의 구조 정보만 사용하여 테이블 조회를 통해 레이어 임베딩을 생성합니다.

7.1 GNN VS MLP/CNN/RNN

그래프 데이터의 노드 이웃에는 두 가지 특성이 있습니다. 첫째, 숫자가 불확실하고, 두 번째는 순서입니다. 따라서 MLP/CNN/RNN은 이러한 비-변수를 직접 처리할 수 없습니다. 유럽 데이터는 GNN으로만 모델링할 수 있습니다. 실제로 GNN은 보다 일반적인 모델로 간주될 수 있습니다. 예를 들어 RNN은 선형 그래프의 GNN과 동일하고 Transformer는 전체 그래프의 GNN과 동일합니다.

7.2 GNN VS 그래프 임베딩

많은 그래프 임베딩 방법이 GNN 이전에 등장했으며 검색 서비스의 벡터 호출 단계에서 널리 사용됩니다. 이러한 방법은 원래 Item2Vec에서 Node2Vec까지 Word2vec에서 영감을 얻었습니다. 동질성과 구조의 균형을 맞추는 것, 그래프의 이질성을 기반으로 한 MetaPath2Vec의 개선, 행동 데이터의 희소성을 완화하기 위한 속성 데이터 도입까지 이러한 방법은 모두 Skip-Gram 패러다임을 따릅니다.

이러한 방법에 비해 GNN은 대상 작업을 기반으로 엔드투엔드 훈련을 할 수 있는 반면, 그래프 임베딩은 사전 훈련에 더 가깝습니다. 특히 비즈니스 시나리오에서 학습한 임베딩은 대상 작업과 반드시 관련이 있는 것은 아닙니다. 표본 크기가 크면 엔드투엔드 훈련으로 얻은 임베딩이 사전 훈련으로 얻은 임베딩보다 더 효과적입니다.

GNN의 계층적 네트워크 구조는 GCN+Attenotallow=GAT와 같은 다른 딥 러닝 기술과 쉽게 결합할 수 있습니다. GNN은 귀납적 작업, 즉 그래프의 구조가 변경되고 일부 새로운 노드가 추가되는 경우 Graph Embedding 방법인 경우 모델을 재교육해야 하며 GNN은 GraphSage Node와 유사한 방법을 사용할 수 있습니다. -Wise Sampling, 이미 학습된 모델을 이용하여 새로운 노드를 직접 추론하고, 메시지 전달 과정에서 다양한 기능을 활용할 수 있습니다.

7.3 GNN VS Feature Concat & Collaborative Filtering & Proximity Loss

Feature Concat은 기능을 서로 연결한 다음 기능 교차를 통해 1차 속성 연관 정보를 학습하는 것을 의미합니다. Collaborative Filtering은 사용자의 과거 행동을 통해 1차 행동 상관 정보도 학습할 수 있습니다. 근접 손실은 인접한 노드를 더 유사하게 만들기 위해 손실 함수에 정규 항을 추가하는 것을 의미하지만 한편으로는 암시적인 방법이지만, 다른 한편으로는 고차 유사성 관계가 학습되었는지 확인하려면 다음을 추가해야 합니다. more complex K-order 정규항 역시 GCN이 제안되었을 때의 출발점 중 하나이다. 이 세 가지 방법에 비해 GNN은 여러 레이어를 쌓아서 고차 상관 정보를 명시적으로 학습할 수 있습니다.

그래프 신경망 설계에서 반드시 충족해야 할 핵심 조건이 있는데, 바로 순열 불변성(permutation invariance) 또는 순열 동등성(permutation Equivariance)입니다. 즉, 설계된 함수가 그래프 데이터를 처리할 때 노드 순서에 영향을 받지 않거나, 입력 중 순차 변환 영역의 출력 순서는 일관됩니다.

8. 요약

그래프는 엔터티를 제한 없이 연결할 수 있는 가장 유연한 연결 방법입니다. 그래프 컴퓨팅(Graph Computing)은 대용량 데이터 중 그래프 데이터를 효율적으로 계산, 저장, 관리하는 방법을 연구하는 분야로 자본시장 위험 관리, 생명과학 연구, 헬스케어 제공, 모니터링 등 광범위한 비즈니스 시나리오에 적용할 수 있다. 도로사고 대응, 지능형 인프라 관리 등 대규모 데이터를 효율적으로 처리하는 그래프 컴퓨팅은 소셜 네트워크 분석, 의미 웹 분석, 생물학적 정보 네트워크 분석, 자연어 처리 등 새로운 응용 분야의 개발을 촉진할 수 있습니다.