고급 수학 문제를 해결하기 위해 Python을 배우세요

Python은 고급 수학 문제를 해결하므로 어머니는 더 이상 내 공부에 대해 걱정하지 않으셔도 됩니다.

Python을 사용하여 극한, 도함수, 편도함수, 정적분, 부정적분, 이중적분 등의 문제를 해결하세요. . 고급 수학

Sympy는 모든 기능을 갖춘 컴퓨터 대수학 시스템을 목표로 하는 Python 과학 컴퓨팅 라이브러리입니다. SymPy에는 기본 기호 연산부터 미적분학, 대수학, 이산 수학 및 양자 물리학에 이르는 기능이 포함되어 있습니다. LaTeX로 결과를 표시할 수 있습니다.网Sympy 공식 홈페이지 m

• 파이썬으로 고등 수학 문제를 풀면 엄마는 더 이상 학습에 대해 걱정할 필요가 없습니다
• 1. 실기
• • 1.1 기호 기능
  • 1.2 확장 확장
  • 1.3 테일러 전개식 계열
  • 1.4 기호 전개
• 2. 극한을 구합니다
• 3. 미분 차이를 구합니다
• • 3.1 일변량 함수
  • 3.2 다변량 함수
• 4. 통합하세요
• • 4.1 정적분
  • 4.2 부정적분
  • 4.3 이중적분
• 5. 연립방정식을 풀어보세요. 비디오 튜토리얼
)

이 사진을 보면 숨이 막힐 것 같나요? Python이 이 문제를 해결하는 데 도움을 드립니다.

from sympy import *import sympy

x = Symbol("x")y = Symbol("y")

1.1 기호 함수

허수 단위

sympy.I

sympy.E

infinity

sympy.oo

pi

sympy.pi

n번째 근을 찾아보세요

sympy.root(8,3)

대수를 취하세요

sympy.log(1024,2)

찾기 계승

sympy.factorial(4)

삼각함수

sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)

1.2 표현식 확장 Expand

f = (1+x)**3expand(f)

$x^3+3x^2+3x+1$

1.3 泰勒展开公式series

ln(1+x).series(x,0,4)

x − x 2 2 + x 3 3 + O ( x 4 ) \displaystyle x - \frac{x^{2}}{2} + \frac{x^{3}}{3} + O\left(x^{4}오른쪽)x−2xㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ+ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ3ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ(x4)

sin(x).series(x,0,8)

x − x 3 6 + x 5 120 − x 7 5040 + O ( x 8 ) \displaystyle x - \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040} + O\left(x^{8}오른쪽)x−6xㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ+ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ5ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ5040x7ㅋㅋㅋ8)

cos(x).series(x,0,9)

1 − x 2 2 + x 4 24 − x 6 720 + x 8 40320 + O ( x 9 ) \displaystyle 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} - \frac{x^{6}}{720} + \frac{x^{8}}{40320} + O\left(x^{9}오른쪽)1−2xㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ+ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ4ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ720ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ+ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋxㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ+Oㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ)

(1/(1+x)).series(x,0,5)

1 − x + x 2 − x 3 + x 4 + O ( x 5 ) \displaystyle 1 - x + x^{2} - x^{3} + x^{4} + O\left(x^{5}오른쪽) ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋx2ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ3+x4+O(ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ

tan(x).series(x,0,4)

$x+\frac{x^3}{3}+O\left(x^4\right)$

(1/(1-x)).series(x,0,4)

$1+x+x^2+x^3+O\left(x^4\right)$

(1/(1+x)).series(x,0,4)

$1-x+x^2-x^3+O\left(x^4\right)$

1.4 符号展开

a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)

$x^{a+b}$

2. 求极限limit

limit(sin(x)/x,x,0)

$1$

f2=(1+x)**(1/x)

f2

${\left(x+1\right)}^{\frac{1}{x}}$

重要极限

f1=sin(x)/x f2=(1+x)**(1/x)f3=(1+1/x)**x lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)

1 E E

dir可以表示极限的趋近方向

f4 = (1+exp(1/x))f4

$e^{\frac{1}{x}}+1$

lim4 = limit(f4,x,0,dir="-")lim4

$1$

lim5 = limit(f4,x,0,dir="+")lim5

$\infty$

3. 求导diff

diff(函数,自变量,求导次数)

3.1 一元函数

求导问题

diff(sin(2*x),x)

$2\cos \left(2x\right)$

diff(ln(x),x)

$\frac{1}{x}$

3.2 多元函数

求偏导问题

diff(sin(x*y),x,y)

$-xy\sin \left(xy\right)+\cos \left(xy\right)$

4. 积分integrate

4.1 定积分

• 函数的定积分: integrate(函数，(变量，下限，上限))
• 函数的不定积分: integrate(函数,变量)

f = x**2 + 1integrate(f,(x,-1.1))

$-1.54366666666667$

integrate(exp(x),(x,-oo,0))

$1$

4.2 不定积分

f = 1/(1+x*x)integrate(f,x)

$\mathrm{atan}\left(x\right)$

4.3 双重积分

f = (4/3)*x + 2*y integrate(f,(x,0,1),(y,-3,4))

$11.6666666666667$

5. 求解方程组solve

#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])

{x: -1, y: 4}

6. 计算求和式summation

计算求和式可以使用sympy.summation函数，其函数原型为sympy.summation(f, *symbols, **kwargs)

**

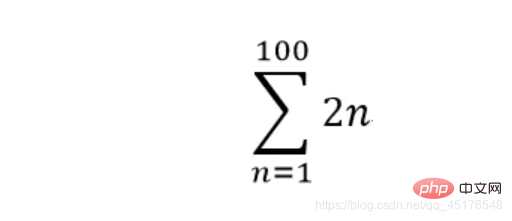
sympy.summation(2 * n,(n,1,100))

10100

到这里就结束了，如果对你有帮助，欢迎点赞关注评论，你的点赞对我很重要。在此也祝愿大家可以把数学学好

相关免费学习推荐：python教程（视频）

위 내용은 고급 수학 문제를 해결하기 위해 Python을 배우세요의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!