연관 규칙 apriori 알고리즘 이해: Apriori 알고리즘은 최초의 연관 규칙 마이닝 알고리즘이자 가장 고전적인 알고리즘으로 레이어별 검색의 반복 방법을 사용하여 데이터베이스의 항목 세트 간의 관계를 찾아 규칙을 형성합니다. 프로세스는 연결로 구성됩니다. [행렬과 유사한 작업]과 가지치기(불필요한 중간 결과 제거)로 구성됩니다.

연관 규칙 선험적 알고리즘 이해:
1. 개념
표 1 슈퍼마켓의 거래 데이터베이스
거래 번호 TID |
고객이 구매한 품목 |
거래번호 TID |
고객이 구매한 품목 |
T1 |
빵, 크림, 우유, 차 |
T6 |
빵 , 차 |
T2 |
빵, 크림, 우유 |
T7 |
맥주, 우유, 차 |
T3 |
케이크, 우유 |
T8 |
빵, 차 |
T4 |
우유, 차 |
T9 |
빵, 크림, 우유, 차 |
T5 |
빵, 케이크, 우유 |
T10 |
빵, 우유, 차 |
정의 1:I={i1,i2,…,im}이라고 가정합니다. 이는 m개의 서로 다른 프로젝트 집합이고 각 ik은project이라고 합니다. 항목 모음I을itemset이라고 합니다. 해당 요소의 수를 항목 집합의 길이라고 하며, 길이가k인 항목 집합을 k-항목 집합이라고 합니다. 예시에서 각 제품은 품목이고 품목 집합은 I={빵, 맥주, 케이크,크림, 우유, 차}이고 I의 길이는 6입니다.
정의 2: 각transactionT는 항목 집합 I의 하위 집합입니다. 각 거래에 해당하는 고유 식별 거래 번호가 있으며 TID로 기록됩니다. 모든 트랜잭션은트랜잭션 데이터베이스D를 구성하며 |D|는 D의 트랜잭션 수와 같습니다. 이 예에는 10개의 트랜잭션이 포함되어 있으므로 |D|=10입니다.
정의 3: 항목 집합X의 경우 count(X⊆T)를 트랜잭션 집합 D의 X를 포함하는 트랜잭션 수로 설정하면 항목 집합 X의지원은 다음과 같습니다.
support(X)=count(X⊆T)/|D|
예제에서X={bread, milk}는 T1, T2, T5, T9 및 T10에 나타나므로 지지도는 0.5입니다.
정의 4:최소 지원은SUPmin으로 기록되는 항목 집합의 최소 지원 임계값으로, 사용자가 관심을 갖는 연결 규칙의 최소 중요성을 나타냅니다.지지도가SUPmin 이상인 항목 집합을 빈발 집합이라고 하며, 길이가k인 빈발 집합을 k-빈번 집합이라고 합니다. SUPmin을 0.3으로 설정하면 예시에서 {빵, 우유}의 지지도는 0.5이므로 2-빈번 세트입니다.
정의 5:연관 규칙은 의미:
R: . 특정 거래에서 아이템세트 X가 등장하면 일정 확률로 Y도 등장함을 나타냅니다. 사용자가 관심을 갖는 연관 규칙은 지지도와 신뢰성이라는 두 가지 기준으로 측정할 수 있습니다.
정의 6
: 연관 규칙R의지원은 트랜잭션 세트에X와 Y가 모두 포함된 트랜잭션 수와 |D|의 비율입니다. 즉,support(X⇒Y)=count(X⋃Y)/|D|
Support는X와 Y가 동시에 나타날 확률을 반영합니다. 연관 규칙의 지원은 빈번한 집합의 지원과 동일합니다.
정의 7
: 연관 규칙R의 경우credibility은X 및 Y가 포함된 트랜잭션 수와 X가 포함된 트랜잭션 수의 비율을 나타냅니다. 즉,confidence(X⇒Y)=support(X⇒Y)/support(X)
Confidence는X가 거래에 포함된 경우 거래에 Y가 포함될 확률을 반영합니다. 일반적으로 사용자는 지지도와 신뢰성이 높은 연관 규칙에만 관심을 갖습니다.
정의 8: 연관 규칙의 최소 지원 및 최소 신뢰도를 SUPmin 및 CONFmin으로 설정합니다. 규칙 R의 지지도와 신뢰도가 SUPmin 및 CONFmin 이상인 경우 이를
강한 연관 규칙이라고 합니다. 연관 규칙 마이닝의 목적은 판매자의 의사결정을 안내하는 강력한 연관 규칙을 찾는 것입니다.이 8가지 정의에는 연관 규칙과 관련된 몇 가지 중요한 기본 개념이 포함되어 있습니다. 연관 규칙 마이닝에는 두 가지 주요 문제가 있습니다.
현재 연구자들은 첫 번째 문제를 주로 연구하고 있습니다. 빈발 집합을 찾는 것은 어렵지만, 빈발 집합을 사용하여 강력한 연관 규칙을 재생성하는 것은 비교적 쉽습니다.
2. 이론적 근거
먼저 빈발 집합의 속성을 살펴보겠습니다.
정리:항목 집합X가 빈발 집합이면 비어 있지 않은 부분 집합도 모두 빈발 집합입니다.
정리에 따르면k-빈번 집합의 항목 집합 X가 주어지면 의 모든 k-1 순서 하위 집합은 항목 하나만 다르며 연결 후 X와 같습니다. 이는 k-1개의 빈번한 집합을 연결하여 생성된 k-후보 집합이 k-빈번 집합을 포함한다는 것을 증명합니다. 동시에, k-후보 집합의 항목 집합 Y에 k-1 빈번 집합에 속하지 않는 k-1 순서 부분 집합이 포함되어 있으면 Y는 빈번 집합이 될 수 없으며 후보 집합에서 제거되어야 합니다. Apriori 알고리즘은 이러한 빈번한 집합의 속성을 활용합니다.
3. 알고리즘 단계:
첫 번째는 테스트 데이터입니다.
목록알고리즘의 단계 다이어그램:
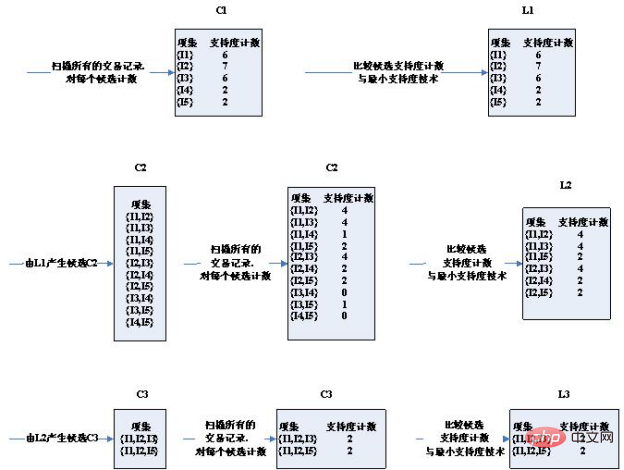
3라운드에서 설정된 후보가 크게 줄어든 것을 볼 수 있습니다. 왜 그럴까요?
후보 세트 선택 시 주의할 점 2가지 조건:
1. 두 개의 K 항목 세트가 연결되는 두 가지 조건은 동일한 K-1 항목이 있어야 한다는 것입니다. 따라서 (I2, I4)와 (I3, I5)는 연결할 수 없습니다. 후보군이 좁아졌습니다.
2. 항목 집합이 빈발 집합인 경우 부분 집합이 아닌 빈발 집합이 없습니다. 예를 들어 (I1, I2)와 (I1, I4)는 (I1, I2, I4)를 얻고 (I1, I2, I4)의 하위 집합 (I1, I4)은 빈번한 집합이 아닙니다. 후보군이 좁아졌습니다.
3차 라운드에서 얻은2개의 후보 세트는 정확히 최소 지지도와 동일한 지지도를 갖습니다. 따라서 모두 빈번한 세트에 포함됩니다.
이제 4라운드의 후보 세트와 빈발 세트 결과가 비어 있는 것을 보면
후보 세트와 빈발 세트가 실제로 비어 있는 것을 확인할 수 있습니다! 3차 라운드를 통해 얻은 빈발집합은 자기연결되어 {I2, I3, I5}의 부분집합을 갖는{I1, I2, I3, I5}를 획득하고, {I2, I3, I5}는 빈발이 아니기 때문이다. 집합이고 만족하지 않음: 빈발 집합의 부분 집합도 빈발 집합의 조건을 가지므로 가지치기를 통해 제거됩니다. 따라서 전체 알고리즘이 종료되고 마지막으로 계산된 빈발 집합이 최종 빈발 집합 결과로 사용됩니다.
즉:['I1,I2,I3', 'I1,I2,I5']
4 . 코드 :
Apriori 알고리즘을 구현하는 Python 코드를 작성합니다. 코드는 다음 두 가지 사항에 주의해야 합니다.
def local_data(file_path): import pandas as pd dt = pd.read_excel(file_path) data = dt['con'] locdata = [] for i in data: locdata.append(str(i).split(",")) # print(locdata) # change to [[1,2,3],[1,2,3]] length = [] for i in locdata: length.append(len(i)) # 计算长度并存储 # print(length) ki = length[length.index(max(length))] # print(length[length.index(max(length))]) # length.index(max(length)读取最大值的位置,然后再定位取出最大值 return locdata,kidef create_C1(data_set): """ Create frequent candidate 1-itemset C1 by scaning data set. Args: data_set: A list of transactions. Each transaction contains several items. Returns: C1: A set which contains all frequent candidate 1-itemsets """ C1 = set() for t in data_set: for item in t: item_set = frozenset([item]) C1.add(item_set) return C1def is_apriori(Ck_item, Lksub1): """ Judge whether a frequent candidate k-itemset satisfy Apriori property. Args: Ck_item: a frequent candidate k-itemset in Ck which contains all frequent candidate k-itemsets. Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets. Returns: True: satisfying Apriori property. False: Not satisfying Apriori property. """ for item in Ck_item: sub_Ck = Ck_item - frozenset([item]) if sub_Ck not in Lksub1: return False return Truedef create_Ck(Lksub1, k): """ Create Ck, a set which contains all all frequent candidate k-itemsets by Lk-1's own connection operation. Args: Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets. k: the item number of a frequent itemset. Return: Ck: a set which contains all all frequent candidate k-itemsets. """ Ck = set() len_Lksub1 = len(Lksub1) list_Lksub1 = list(Lksub1) for i in range(len_Lksub1): for j in range(1, len_Lksub1): l1 = list(list_Lksub1[i]) l2 = list(list_Lksub1[j]) l1.sort() l2.sort() if l1[0:k-2] == l2[0:k-2]: Ck_item = list_Lksub1[i] | list_Lksub1[j] # pruning if is_apriori(Ck_item, Lksub1): Ck.add(Ck_item) return Ckdef generate_Lk_by_Ck(data_set, Ck, min_support, support_data): """ Generate Lk by executing a delete policy from Ck. Args: data_set: A list of transactions. Each transaction contains several items. Ck: A set which contains all all frequent candidate k-itemsets. min_support: The minimum support. support_data: A dictionary. The key is frequent itemset and the value is support. Returns: Lk: A set which contains all all frequent k-itemsets. """ Lk = set() item_count = {} for t in data_set: for item in Ck: if item.issubset(t): if item not in item_count: item_count[item] = 1 else: item_count[item] += 1 t_num = float(len(data_set)) for item in item_count: if (item_count[item] / t_num) >= min_support: Lk.add(item) support_data[item] = item_count[item] / t_num return Lkdef generate_L(data_set, k, min_support): """ Generate all frequent itemsets. Args: data_set: A list of transactions. Each transaction contains several items. k: Maximum number of items for all frequent itemsets. min_support: The minimum support. Returns: L: The list of Lk. support_data: A dictionary. The key is frequent itemset and the value is support. """ support_data = {} C1 = create_C1(data_set) L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data) Lksub1 = L1.copy() L = [] L.append(Lksub1) for i in range(2, k+1): Ci = create_Ck(Lksub1, i) Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data) Lksub1 = Li.copy() L.append(Lksub1) return L, support_datadef generate_big_rules(L, support_data, min_conf): """ Generate big rules from frequent itemsets. Args: L: The list of Lk. support_data: A dictionary. The key is frequent itemset and the value is support. min_conf: Minimal confidence. Returns: big_rule_list: A list which contains all big rules. Each big rule is represented as a 3-tuple. """ big_rule_list = [] sub_set_list = [] for i in range(0, len(L)): for freq_set in L[i]: for sub_set in sub_set_list: if sub_set.issubset(freq_set): conf = support_data[freq_set] / support_data[freq_set - sub_set] big_rule = (freq_set - sub_set, sub_set, conf) if conf >= min_conf and big_rule not in big_rule_list: # print freq_set-sub_set, " => ", sub_set, "conf: ", conf big_rule_list.append(big_rule) sub_set_list.append(freq_set) return big_rule_listif __name__ == "__main__": """ Test """ file_path = "test_aa.xlsx" data_set,k = local_data(file_path) L, support_data = generate_L(data_set, k, min_support=0.2) big_rules_list = generate_big_rules(L, support_data, min_conf=0.4) print(L) for Lk in L: if len(list(Lk)) == 0: break print("="*50) print("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport") print("="*50) for freq_set in Lk: print(freq_set, support_data[freq_set]) print() print("Big Rules") for item in big_rules_list: print(item[0], "=>", item[1], "conf: ", item[2])
파일 형식:
test_aa.xlsx
name con T1 2,3,5T2 1,2,4T3 3,5T5 2,3,4T6 2,3,5T7 1,2,4T8 3,5T9 2,3,4T10 1,2,3,4,5
관련 무료 학습 권장 사항:python 비디오 튜토리얼
T100 I 3 |
T400I1, I2, I4 |
| I1, I3 | |
| I2, I3 | |
| I1, I3 | |
| I1,I2,I3,I5 | |
| I1,I2,I3 |
위 내용은 연관 규칙 선험적 알고리즘을 이해하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!