v8 정렬 소스 코드 해석에 대한 JavaScript 주제 시리즈의 20번째이자 마지막 기사
v8은 Chrome의 JavaScript 엔진으로, 배열 정렬이 완전히 JavaScript로 구현됩니다.
정렬에 사용되는 알고리즘은 배열 길이가 10보다 작거나 같으면 삽입 정렬이 사용됩니다. 배열 길이가 10보다 크면 빠른 정렬이 사용됩니다. (물론 이 진술이 엄격한 것은 아니다).
먼저 삽입 정렬과 퀵 정렬에 대해 살펴보겠습니다.
첫 번째 요소를 정렬된 시퀀스로 처리하고, 배열을 순회한 후, 구성된 정렬된 시퀀스에 후속 요소를 차례로 삽입합니다.
function insertionSort(arr) {
for (var i = 1; i < arr.length; i++) {
var element = arr[i];
for (var j = i - 1; j >= 0; j--) {
var tmp = arr[j];
var order = tmp - element;
if (order > 0) {
arr[j + 1] = tmp;
} else {
break;
}
}
arr[j + 1] = element;
}
return arr;
}
var arr = [6, 5, 4, 3, 2, 1];
console.log(insertionSort(arr));시간 복잡도는 알고리즘을 실행하는 데 필요한 계산 작업량을 의미합니다. 일반적인 상황에서는 입력 값의 크기가 무한대에 가까워지는 상황을 살펴봅니다. 알고리즘의 기본 작업이 반복되는 횟수는 문제 크기 n의 함수입니다.
최고의 경우: 오름차순 배열, 시간 복잡도: O(n)
최악의 경우: 내림차순 배열, 시간 복잡도: O(n²)
안정성은 동일함을 의미 정렬 후 상대 위치.
불안정한 정렬 알고리즘의 경우 불안정성을 설명하기 위해 예를 제공하고 안정적인 정렬 알고리즘의 경우 안정적인 특성을 얻으려면 알고리즘을 분석해야 합니다.
예를 들어 [3, 3, 1]은 정렬 후에도 여전히 [3, 3, 1]이지만 실제로는 두 번째 3이 첫 번째 3보다 앞에 있으므로 이는 불안정한 정렬 알고리즘입니다.
삽입 정렬은 안정적인 알고리즘입니다.
배열을 정렬하려고 하거나 문제 크기가 상대적으로 작은 경우 삽입 정렬이 더 효율적입니다. 이것이 v8이 배열 길이가 10보다 작거나 같을 때 삽입 정렬을 사용하는 이유입니다.
요소를 "기준선"으로 선택하세요.
"기준선"보다 작은 요소는 "기준선"보다 큰 "기준선" 요소의 왼쪽으로 이동됩니다. 기준선"이 오른쪽의 "기준선" "으로 이동됩니다.
모든 하위 집합에 하나의 요소만 남을 때까지 "기준선"의 왼쪽과 오른쪽에 있는 두 하위 집합에 대해 첫 번째와 두 번째 단계를 반복합니다.
예와 다음 구현 방법은 Ruan Yifeng 선생님의 "Javascript 구현 of Quicksort"에서 따왔습니다.
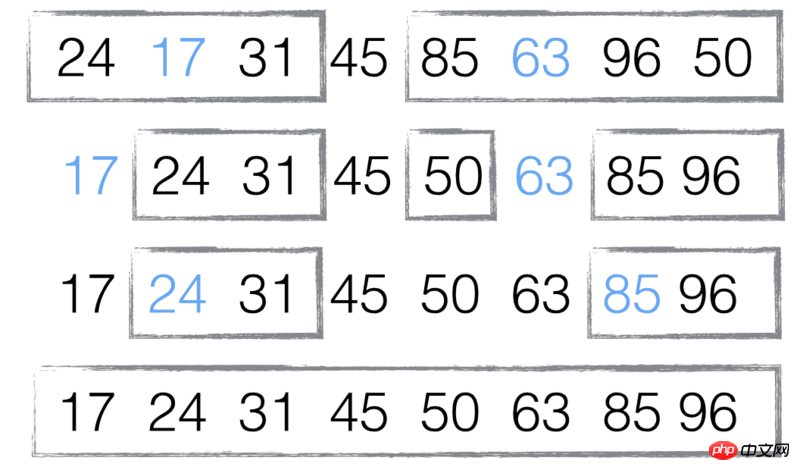
배열 [85, 24, 63, 45, 17, 31, 96, 50] 예:
첫 번째 단계는 중간 요소 45를 "기본"으로 선택하는 것입니다. (기준값은 임의로 선택할 수 있지만 중간값을 선택하는 것이 이해하기 쉽습니다.)

두 번째 단계는 각 요소를 "기준선"과 순서대로 비교하여 두 개의 하위 집합, 하나의 하위 집합을 구성하는 것입니다. "45 미만"이고 다른 하나는 "45 이상"입니다.

세 번째 단계는 모든 하위 집합에 하나의 요소만 남을 때까지 두 하위 집합에 대해 첫 번째와 두 번째 단계를 반복하는 것입니다.
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
// 取数组的中间元素作为基准
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};그러나 이 구현에는 왼쪽 및 오른쪽 하위 집합을 저장하기 위한 추가 공간이 필요하므로 내부 정렬 구현도 있습니다.
내부 정렬 구현 다이어그램을 살펴보겠습니다.
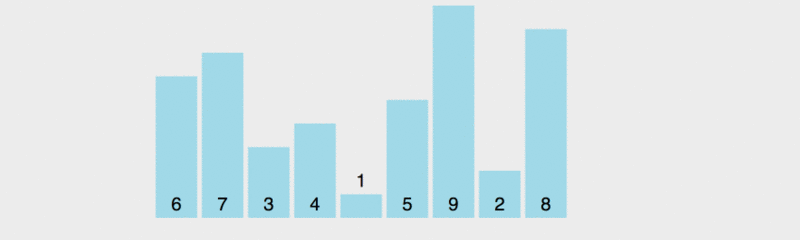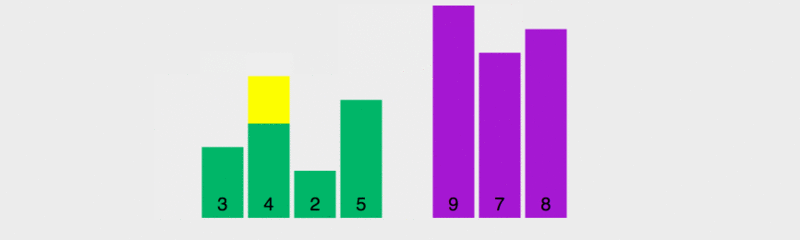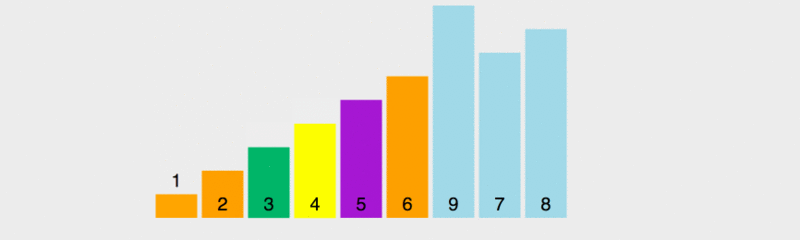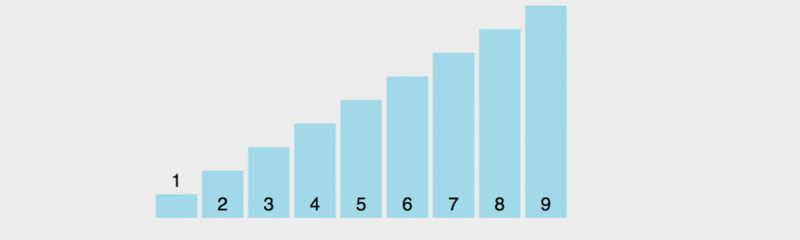
퀵 정렬의 원리를 모두가 이해할 수 있도록 실행 속도를 늦췄습니다.
이 다이어그램에서 벤치마크의 값 규칙은 가장 왼쪽 요소를 취하는 것입니다. 노란색은 현재 벤치마크를 나타내고, 녹색은 벤치마크보다 작은 요소를 나타내고, 보라색은 벤치마크보다 큰 요소를 나타냅니다.
녹색 요소가 피벗 바로 오른쪽에 있고 보라색 요소가 뒤쪽으로 이동한 다음 피벗과 마지막 녹색 요소가 이때 교체된다는 것을 알 수 있습니다. 올바른 위치, 즉 이전 요소는 모두 기준 값보다 작으면 이후의 모든 요소는 기준 값보다 커집니다. 그런 다음 이전 및 다음 여러 요소를 기반으로 정렬합니다.
function quickSort(arr) {
// 交换元素
function swap(arr, a, b) {
var temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
function partition(arr, left, right) {
var pivot = arr[left];
var storeIndex = left;
for (var i = left + 1; i <= right; i++) {
if (arr[i] < pivot) {
swap(arr, ++storeIndex, i);
}
}
swap(arr, left, storeIndex);
return storeIndex;
}
function sort(arr, left, right) {
if (left < right) {
var storeIndex = partition(arr, left, right);
sort(arr, left, storeIndex - 1);
sort(arr, storeIndex + 1, right);
}
}
sort(arr, 0, arr.length - 1);
return arr;
}
console.log(quickSort(6, 7, 3, 4, 1, 5, 9, 2, 8))빠른 정렬은 불안정한 정렬입니다. 정렬이 불안정하다는 것을 증명하려면 예만 들면 됩니다.
그럼 하나 키워보자~
就以数组 [1, 2, 3, 3, 4, 5] 为例,因为基准的选择不确定,假如选定了第三个元素(也就是第一个 3) 为基准,所有小于 3 的元素在前面,大于等于 3 的在后面,排序的结果没有问题。可是如果选择了第四个元素(也就是第二个 3 ),小于 3 的在基准前面,大于等于 3 的在基准后面,第一个 3 就会被移动到 第二个 3 后面,所以快速排序是不稳定的排序。
阮一峰老师的实现中,基准取的是中间元素,而原地排序中基准取最左边的元素。快速排序的关键点就在于基准的选择,选取不同的基准时,会有不同性能表现。
快速排序的时间复杂度最好为 O(nlogn),可是为什么是 nlogn 呢?来一个并不严谨的证明:
在最佳情况下,每一次都平分整个数组。假设数组有 n 个元素,其递归的深度就为 log2n + 1,时间复杂度为 O(n)[(log2n + 1)],因为时间复杂度考察当输入值大小趋近无穷时的情况,所以会忽略低阶项,时间复杂度为:o(nlog2n)。
如果一个程序的运行时间是对数级的,则随着 n 的增大程序会渐渐慢下来。如果底数是 10,lg1000 等于 3,如果 n 为 1000000,lgn 等于 6,仅为之前的两倍。如果底数为 2,log21000 的值约为 10,log21000000 的值约为 19,约为之前的两倍。我们可以发现任意底数的一个对数函数其实都相差一个常数倍而已。所以我们认为 O(logn)已经可以表达所有底数的对数了,所以时间复杂度最后为: O(nlogn)。
而在最差情况下,如果对一个已经排序好的数组,每次选择基准元素时总是选择第一个元素或者最后一个元素,那么每次都会有一个子集是空的,递归的层数将达到 n,最后导致算法的时间复杂度退化为 O(n²)。
这也充分说明了一个基准的选择是多么的重要,而 v8 为了提高性能,就对基准的选择做了很多优化。
v8 选择基准的原理是从头和尾之外再选择一个元素,然后三个值排序取中间值。
当数组长度大于 10 但是小于 1000 的时候,取中间位置的元素,实现代码为:
// 基准的下标 // >> 1 相当于除以 2 (忽略余数) third_index = from + ((to - from) >> 1);
当数组长度大于 1000 的时候,每隔 200 ~ 215 个元素取一个值,然后将这些值进行排序,取中间值的下标,实现的代码为:
// 简单处理过
function GetThirdIndex(a, from, to) {
var t_array = new Array();
// & 位运算符
var increment = 200 + ((to - from) & 15);
var j = 0;
from += 1;
to -= 1;
for (var i = from; i < to; i += increment) {
t_array[j] = [i, a[i]];
j++;
}
// 对随机挑选的这些值进行排序
t_array.sort(function(a, b) {
return comparefn(a[1], b[1]);
});
// 取中间值的下标
var third_index = t_array[t_array.length >> 1][0];
return third_index;
}也许你会好奇 200 + ((to - from) & 15) 是什么意思?
& 表示是按位与,对整数操作数逐位执行布尔与操作。只有两个操作数中相对应的位都是 1,结果中的这一位才是 1。
以 15 & 127 为例:
15 二进制为: (0000 1111)
127 二进制为:(1111 1111)
按位与结果为:(0000 1111)= 15
所以 15 & 127 的结果为 15。
注意 15 的二进制为: 1111,这就意味着任何和 15 按位与的结果都会小于或者等于 15,这才实现了每隔 200 ~ 215 个元素取一个值。
终于到了看源码的时刻!源码地址为:https://github.com/v8/v8/blob/master/src/js/array.js#L758。
function InsertionSort(a, from, to) {
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
};
function QuickSort(a, from, to) {
var third_index = 0;
while (true) {
// Insertion sort is faster for short arrays.
if (to - from <= 10) {
InsertionSort(a, from, to);
return;
}
if (to - from > 1000) {
third_index = GetThirdIndex(a, from, to);
} else {
third_index = from + ((to - from) >> 1);
}
// Find a pivot as the median of first, last and middle element.
var v0 = a[from];
var v1 = a[to - 1];
var v2 = a[third_index];
var c01 = comparefn(v0, v1);
if (c01 > 0) {
// v1 < v0, so swap them.
var tmp = v0;
v0 = v1;
v1 = tmp;
} // v0 <= v1.
var c02 = comparefn(v0, v2);
if (c02 >= 0) {
// v2 <= v0 <= v1.
var tmp = v0;
v0 = v2;
v2 = v1;
v1 = tmp;
} else {
// v0 <= v1 && v0 < v2
var c12 = comparefn(v1, v2);
if (c12 > 0) {
// v0 <= v2 < v1
var tmp = v1;
v1 = v2;
v2 = tmp;
}
}
// v0 <= v1 <= v2
a[from] = v0;
a[to - 1] = v2;
var pivot = v1;
var low_end = from + 1; // Upper bound of elements lower than pivot.
var high_start = to - 1; // Lower bound of elements greater than pivot.
a[third_index] = a[low_end];
a[low_end] = pivot;
// From low_end to i are elements equal to pivot.
// From i to high_start are elements that haven&#39;t been compared yet.
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
var order = comparefn(element, pivot);
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
} else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = comparefn(top_elem, pivot);
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
}
}
if (to - high_start < low_end - from) {
QuickSort(a, high_start, to);
to = low_end;
} else {
QuickSort(a, from, low_end);
from = high_start;
}
}
}
var arr = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0];
function comparefn(a, b) {
return a - b
}
QuickSort(arr, 0, arr.length)
console.log(arr)我们以数组 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0] 为例,分析执行的过程。
1.执行 QuickSort 函数 参数 from 值为 0,参数 to 的值 11。
2.10 < to - from < 1000 第三个基准元素的下标为 (0 + 11 >> 1) = 5,基准值 a[5] 为 5。
3.比较 a[0] a[10] a[5] 的值,然后根据比较结果修改数组,数组此时为 [0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10]
4.将基准值和数组的第(from + 1)个即数组的第二个元素互换,此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10],此时在基准值 5 前面的元素肯定是小于 5 的,因为第三步已经做了一次比较。后面的元素是未排序的。
我们接下来要做的就是把后面的元素中小于 5 的全部移到 5 的前面。
5.然后我们进入 partition 循环,我们依然以这个数组为例,单独抽出来写个 demo 讲一讲
// 假设代码执行到这里,为了方便演示,我们直接设置 low_end 等变量的值
// 可以直接复制到浏览器中查看数组变换效果
var a = [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]
var low_end = 1;
var high_start = 10;
var pivot = 5;
console.log(&#39;起始数组为&#39;, a)
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
console.log(&#39;循环当前的元素为:&#39;, a[i])
var order = element - pivot;
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
console.log(a)
}
else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = top_elem - pivot;
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
console.log(a)
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
console.log(a)
}
}
console.log(&#39;最后的结果为&#39;, a)
console.log(low_end)
console.log(high_start)6.此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10],循环从第三个元素开始,a[i] 的值为 8,因为大于基准值 5,即 order > 0,开始执行 do while 循环,do while 循环的目的在于倒序查找元素,找到第一个小于基准值的元素,然后让这个元素跟 a[i] 的位置交换。
第一个小于基准值的元素为 1,然后 1 与 8 交换,数组变成 [0, 5, 1, 7, 6, 9, 4, 3, 2, 8, 10]。high_start 的值是为了记录倒序查找到哪里了。
7. 이때 a[i]의 값은 1이 되고, 1을 기준값 5로 바꾸면 배열은 [0, 1, 5, 7, 6, 9, 4, 3이 됩니다. , 2 , 8, 10]에서 low_end의 값은 1씩 증가합니다. low_end의 값은 기준값의 위치를 기록하기 위한 것입니다. [0, 1, 5, 7, 6, 9, 4, 3, 2, 8, 10],low_end 的值加 1,low_end 的值是为了记录基准值的所在位置。
8.循环接着执行,遍历第四个元素 7,跟第 6、7 的步骤一致,数组先变成 [0, 1, 5, 2, 6, 9, 4, 3, 7, 8, 10],再变成 [0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]
9.遍历第五个元素 6,跟第 6、7 的步骤一致,数组先变成 [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10],再变成 [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]
10.遍历第六个元素 9,跟第 6、7 的步骤一致,数组先变成 [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10],再变成 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]
11.在下一次遍历中,因为 i == high_start,意味着正序和倒序的查找终于找到一起了,后面的元素肯定都是大于基准值的,此时退出循环
12.遍历后的结果为 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10],在基准值 5 前面的元素都小于 5,后面的元素都大于 5,然后我们分别对两个子集进行 QuickSort
13.此时 low_end 值为 5,high_start 值为 6,to 的值依然是 10,from 的值依然是 0,to - high_start < low_end - from 的结果为 true,我们对 QuickSort(a, 6, 10),即对后面的元素进行排序,但是注意,在新的 QuickSort 中,因为 from - to 的值小于 10,所以这一次其实是采用了插入排序。所以准确的说,当数组长度大于 10 的时候,v8 采用了快速排序和插入排序的混合排序方法。
14.然后 to = low_end
[0, 1, 5, 2, 6, 9, 4, 3, 7이 됩니다. , 8, 10]이 되고 [0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]9이 됩니다. 요소 6은 6단계 및 7단계와 동일합니다. 배열은 먼저 [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10]이 된 다음 [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]10. 6단계와 7단계와 동일하게 여섯 번째 요소 9를 탐색합니다. 처음에는 [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10]이 되고, 그 다음은 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]11. 다음 순회에서는 i == high_start이므로 정방향 검색과 역방향 검색이 최종적으로 함께 발견된다는 의미이며 다음 요소는 반드시 벤치마크 값보다 크면 지금 루프를 종료하세요 12. 순회 후 결과는 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10] code> , 기본 값 5 앞의 요소는 모두 5보다 작고 뒤의 요소는 모두 5보다 큰 경우 두 하위 집합에 대해 각각 QuickSort를 수행합니다13 이때 low_end 값은 5입니다. , high_start 값은 6이고 to 값은 여전히 10이고 from 값은 여전히 0이며 to - high_start < low_end - from 의 결과는 true입니다. >, 우리는 QuickSort(a, 6, 10)을 사용합니다. 시간. 즉,배열 길이가 10보다 큰 경우 v8에서는 퀵 정렬과 삽입 정렬이라는 하이브리드 정렬 방법을 사용합니다.  14. 그러면
14. 그러면 to = low_end는 5로 설정됩니다. while(true) 때문에 to - from의 값은 5이고 InsertionSort(a)가 다시 실행됩니다. , 0, 5), 즉 참조 값 이전의 요소에 대해 삽입 정렬을 수행합니다.
15. to - from <= 10이라는 판단에 return 문이 있으므로 while 루프가 종료됩니다.
16.v8 배열에 대해 빠른 정렬을 수행한 후 두 하위 집합에 대해 각각 삽입 정렬을 수행하고 마지막으로 배열을 올바르게 정렬된 배열로 수정합니다.
비교
마지막으로 삽입 정렬과 빠른 정렬을 경험하기 위한 도식을 살펴보겠습니다.

사진 출처: https://www.toptal.com/developers/sorting-algorithms🎜🎜특별 시리즈 🎜🎜JavaScript 특별 주제 시리즈 디렉토리 주소: https://github.com/mqyqingfeng/Blog. 🎜🎜JavaScript 주제 시리즈는 약 20개 기사로 예상되며 주로 손떨림 방지, 조절, 중복 제거, 유형 판단, 복사, 최대값, 평면화, 카레, 재귀 등 일상적인 개발에서 일부 기능적 포인트의 구현을 연구합니다. 및 무질서, 정렬 등. (xi) 밑줄 및 jQuery 구현을 연구하는 것이 특징입니다. 🎜🎜🎜🎜🎜🎜🎜위 내용은 JavaScript의 v8 정렬 소스 코드 관련 문제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!