HTML5 Academy-Coder: "Algorithm Journey"의 이전 호에서 버블 정렬 방법과 선택 정렬 방법 모두 시간 복잡도가 O(n^)인 "느린" 정렬 방법을 알려드렸습니다. 2) 정렬. 오늘은 다양한 정렬 알고리즘 중 가장 널리 사용되고 빠른 정렬 알고리즘인 퀵 정렬(평균 시간 복잡도는 O(n logn))에 대해 알려드리고자 합니다.
Tips 1: "알고리즘"과 "정렬"에 대한 기본 지식은 이전 "선택 정렬 방법"에서 자세히 설명했습니다. 기사 마지막에 해당 기사 링크를 클릭하면 볼 수 있습니다. 여기서는 반복하지 않겠습니다.
팁 2: 달리 지정하지 않는 한, 이 글의 퀵 정렬은 작은 것부터 큰 것 순으로 정렬됩니다.
퀵 정렬은 일반적으로 분할 정복 방법이라고 불리는 분할 정복 전략을 채택한 분할 및 교환 정렬입니다.
기본 아이디어: 원래 문제를 크기는 더 작지만 구조는 원래 문제와 유사한 여러 하위 문제로 분해합니다. 이러한 하위 문제를 재귀적으로 해결한 다음 이러한 하위 문제의 결과를 원래 문제의 결과와 결합합니다.
"밑"으로 숫자를 선택하세요.
"밑"보다 작은 모든 숫자는 "밑"보다 크거나 같은 모든 숫자가 "밑"의 왼쪽으로 이동됩니다.
이 이동이 끝나면 "기준선"은 두 시퀀스의 중간에 있게 되며 더 이상 후속 정렬에 참여하지 않게 됩니다.
"기준선"의 왼쪽과 오른쪽에 있는 두 개의 하위 시퀀스 모든 하위 시퀀스에 하나의 숫자만 남을 때까지 위 단계를 반복합니다.
기존 시퀀스 [8, 4, 7, 2, 0, 3, 1]가 있습니다. 다음은 퀵 정렬 방법을 사용하여 정렬하는 방법을 보여줍니다.

먼저 벤치마크의 인덱스 값을 얻은 다음 스플라이스 배열 방식을 사용하여 벤치마크 값을 꺼냅니다.

팁: 이 예에서는 벤치마크의 인덱스 값 =parseInt(시퀀스 길이/2)
팁: splice 메서드는 원래 배열을 변경합니다. 예를 들어 arr = [1, 2, 3]; 기본 인덱스 값은 1이고 기본 값은 2이며 원래 배열은 arr = [1, 3]이 됩니다.
비교 "기준선" 크기로 두 개의 하위 시퀀스로 분할됩니다.
"기준선"보다 작은 숫자는 leftArr 배열에 저장되고 "기준선"보다 크거나 같은 숫자는 rightArr 배열에 저장됩니다

팁 : 물론 "benchmark"라는 숫자는 leftArr에 저장되고, "benchmark"보다 큰 숫자는 rightArr에 저장됩니다.
시퀀스를 순회하고 각 숫자를 다음과 비교해야 하기 때문입니다. "벤치마크"에서는 for 문을 사용하여

함수를 정의하고 형식 매개변수를 사용하여 배열을 수신합니다
function QuickSort(arr) { };
하위 시퀀스를 순회하는 재귀 호출을 구현하고, concat 배열 메서드를 사용합니다. 하위 시퀀스를 결합한 결과

재귀 호출 중에, 하위 시퀀스의 길이가 1과 같으면 재귀 호출이 중지되고 현재 배열이 반환됩니다.


최악의 시나리오: 매번 선택되는 "기준선"은 시퀀스에서 가장 작은 숫자/가장 큰 숫자입니다. 이 상황은 버블 정렬 방법과 유사하며(한 번에 하나의 숫자[기본 번호]의 순서만 결정할 수 있음), 시간 복잡도는 O(n^2)
가장 좋은 경우: "기준선"이 각각 선택됩니다. time은 시퀀스의 중간 숫자(위치의 중간이 아닌 중앙값)이며, 현재 시퀀스는 매번 동일한 길이의 두 하위 시퀀스로 나뉩니다. 이때 처음에는 두 개의 하위 시퀀스 n/2와 n/2가 있고, 두 번째에는 n/4, n/4, n/4, n/4 등 4개의 하위 시퀀스가 있으므로 n개의 숫자가 필요합니다. 정렬을 완료하는 데 필요한 총 logn 횟수(2^x=n, x=logn), n의 복잡도를 가질 때마다 시간 복잡도는 O(n logn)
최악의 경우: n -1번의 재귀 호출이 필요하고 공간 복잡도는 O(n)
최상의 경우: logn 재귀 호출이 필요하며 공간 복잡도는 O(logn)
Quicksort는 불안정한 정렬 알고리즘입니다
예: 기존 시퀀스는 [1, 0, 1, 3]이고 "기준선" 번호는 두 번째 1
으로 선택됩니다. 첫 번째 라운드 이후 비교하면 [0, 1, 1, 3]이 되고, 왼쪽 수열은 [0], 오른쪽 수열은 [1, 3]이 됩니다. (오른쪽 수열의 1이 앞의 1이 됩니다)
아닙니다. 찾기 어렵습니다. 원래 시퀀스에 있는 두 개의 1의 순서가 파괴되고 순서가 변경됩니다. 이는 당연히 "불안정한" 정렬 알고리즘입니다
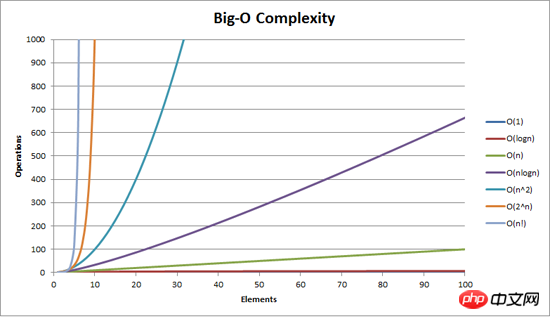
이전 기사 "버블 정렬 방법"에서 우리는 자세히 설명 O가 뭔지 여기서는 길게 말 안하고 사진만 보세요
위 내용은 퀵 정렬을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!