Python의 8가지 정렬 알고리즘 요약(2부)

이 글은 주로 Python으로 구현된 8가지 정렬 알고리즘 중 두 번째 부분을 자세히 소개합니다. 참고할만한 가치가 있으니 관심 있는 친구들은 참고하세요

이 글은 이전 블로그에서 Python으로 구현된 8가지 정렬 알고리즘 1부에 이어 계속됩니다. Python을 사용하여 8가지 주요 정렬 알고리즘 중 나머지 4개(퀵 정렬, 힙 정렬, 병합 정렬, 기수 정렬

5, 퀵 정렬

)를 구현하려면 일반적으로 퀵 정렬은 동일한 크기 순서로 간주됩니다( O(nlog2n) )은 정렬 방법 중 평균 성능이 가장 좋습니다.

알고리즘 아이디어:

우리는 오름차순으로 정렬해야 하는 정렬되지 않은 데이터 집합 a[1], a[2],...a[n]을 알고 있습니다. 먼저, 모든 데이터 a[x]가 벤치마크로 사용됩니다. a[x]를 다른 데이터와 비교하여 a[x]가 데이터의 k번째 위치에 오도록 정렬하고, a[1]~a[k-1] a[x]의 각 데이터를 사용하고 각각 a[1]~a[k-1] 및 a[k+1]~a에 분할 정복 전략을 사용합니다. [n]두 개의 데이터 세트를 빠르게 정렬합니다.
장점: 매우 빠르고 데이터 이동이 적습니다.
단점: 불안정합니다.

파이썬 코드 구현:

def quick_sort(list):
  little = []
  pivotList = []
  large = []
  # 递归出口
  if len(list) <= 1:
    return list
  else:
    # 将第一个值做为基准
    pivot = list[0]
    for i in list:
      # 将比基准小的值放到less数列
      if i < pivot:
        little.append(i)
      # 将比基准大的值放到more数列
      elif i > pivot:
        large.append(i)
      # 将和基准相同的值保存在基准数列
      else:
        pivotList.append(i)
    # 对less数列和more数列继续进行快速排序
    little = quick_sort(little)
    large = quick_sort(large)
    return little + pivotList + large

다음 코드는 "파이썬 요리책 2판"의 세 줄에서 파이썬 퀵 정렬을 구현한 것입니다.

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def quick_sort(list):
  if len(list) <= 1:
    return list
  else:
    pivot = list[0]
    return quick_sort([x for x in list[1:] if x < pivot]) + \
        [pivot] + \
        quick_sort([x for x in list[1:] if x >= pivot])

실행 중인 테스트 결과의 스크린샷:

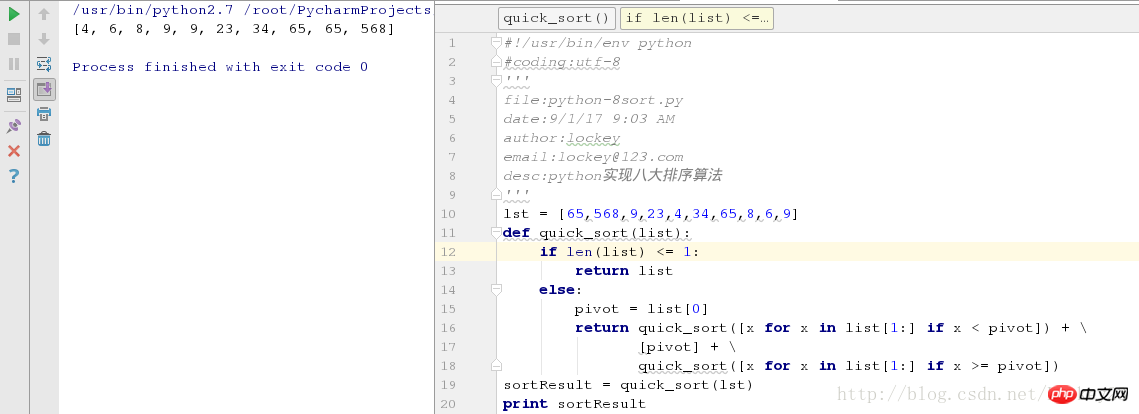
알겠습니다. 한 줄에 더 간소화된 구문 설탕이 있습니다.

quick_sort = 람다 xs : ( (len(xs) <= 1 및 [ xs]) 또는 [quick_sort( [x for x in xs[1:] if x < xs[0]] ) + [xs[0]] +quick_sort( [x for x in xs[1:] if x > ;= xs[0]] ) ] )[0]

초기 시퀀스가 ​​키순으로 정렬되거나 기본적으로 정렬되면 퀵 정렬은 버블 정렬로 변질됩니다. 이를 개선하기 위해 일반적으로 벤치마크 레코드는 "3개의 중간을 취하는 방식"을 사용하여 선택됩니다. 즉, 두 끝점을 중심으로 하는 3개의 레코드 키와 정렬 간격의 중간점을 지점 레코드로 조정합니다. Quicksort는 불안정한 정렬 방법입니다.

개선된 알고리즘에서는 길이가 k보다 큰 하위 시퀀스에 대해서만 퀵 정렬을 재귀적으로 호출하여 원래 시퀀스를 기본적으로 정렬한 다음 삽입 정렬 알고리즘을 사용하여 전체 기본 정렬 시퀀스를 정렬합니다. 개선된 알고리즘의 시간 복잡도는 감소되었으며, k 값이 약 8일 때 개선된 알고리즘이 가장 좋은 성능을 갖는다는 것이 실습을 통해 입증되었습니다.

6. 힙 정렬

힙 정렬은 직접 선택 정렬을 효과적으로 개선한 트리 선택 정렬입니다.

장점: 높은 효율성
단점: 불안정

힙의 정의에 따라: n 요소의 시퀀스(h1, h2,...,hn), (hi>=h2i,hi> =2i인 경우에만) +1) 또는 (hi<=h2i,hi<=2i+1) (i=1,2,...,n/2)을 힙이라고 합니다. 여기서는 이전 조건을 충족하는 힙만 논의합니다. 힙의 정의를 보면 힙의 최상위 요소(즉, 첫 번째 요소)가 가장 큰 항목(빅탑 힙)이어야 함을 알 수 있습니다. 완전한 이진 트리는 힙의 구조를 매우 직관적으로 표현할 수 있습니다. 힙의 맨 위는 루트이고 나머지는 왼쪽 하위 트리와 오른쪽 하위 트리입니다.

알고리즘 아이디어:

처음에는 정렬할 숫자의 순서를 순차적으로 저장된 이진 트리로 간주하고 저장 순서를 조정하여 힙을 만듭니다. 가장 크다. 그런 다음 루트 노드를 힙의 마지막 노드로 바꿉니다. 그런 다음 이전 (n-1) 숫자를 다시 조정하여 힙을 형성합니다. 그런 식으로 두 개의 노드만 있는 힙이 있을 때까지 계속해서 교환되고, 마지막으로 n개의 노드로 구성된 순서화된 시퀀스가 ​​얻어집니다. 알고리즘 설명에 따르면 힙 정렬에는 두 가지 프로세스가 필요합니다. 하나는 힙을 설정하는 것이고, 다른 하나는 힙의 상단과 힙의 마지막 요소 사이의 위치를 ​​교환하는 것입니다. 따라서 힙 정렬은 두 가지 기능으로 구성됩니다. 하나는 힙을 구축하기 위한 침투 함수이고, 다른 하나는 정렬을 구현하기 위해 침투 함수를 반복적으로 호출하는 함수입니다.

Python 코드 구현:

# -*- coding: UTF-8 -*-
'''
Created on 2017年9月2日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def adjust_heap(lists, i, size):# 调整堆
  lchild = 2 * i + 1;rchild = 2 * i + 2
  max = i
  if i < size / 2:
    if lchild < size and lists[lchild] > lists[max]:
      max = lchild
    if rchild < size and lists[rchild] > lists[max]:
      max = rchild
    if max != i:
      lists[max], lists[i] = lists[i], lists[max]
      adjust_heap(lists, max, size)
def build_heap(lists, size):# 创建堆
  halfsize = int(size/2)
  for i in range(0, halfsize)[::-1]:
    adjust_heap(lists, i, size)
def heap_sort(lists):# 堆排序
  size = len(lists)
  build_heap(lists, size)
  for i in range(0, size)[::-1]:
    lists[0], lists[i] = lists[i], lists[0]
    adjust_heap(lists, 0, i)
    print(lists)

결과 예:

7. 병합 정렬

알고리즘 아이디어:

병합 정렬은 병합 작업을 기반으로 하는 효과적인 알고리즘입니다. 이 알고리즘은 다음과 같습니다. 분할 및 정복 방법을 사용하는 매우 일반적인 응용 프로그램입니다. 이미 정렬된 하위 시퀀스를 병합하여 완전히 정렬된 시퀀스를 얻습니다. 즉, 먼저 각 하위 시퀀스를 순서대로 만든 다음 하위 시퀀스 세그먼트를 순서대로 만듭니다. 두 개의 순서 목록이 하나의 순서 목록으로 병합되는 경우 이를 양방향 병합이라고 합니다.

병합 과정은 다음과 같습니다: a[i]와 a[j]의 크기를 비교하고, a[i]≤a[j]인 경우 첫 번째 순서 목록의 요소 a[i]를 r[k ]에 복사합니다. i와 k에 각각 1을 추가합니다. 그렇지 않으면 두 번째 순서 목록의 a[j] 요소를 r[k]에 복사하고 j와 k에 각각 1을 추가하는 식으로 계속됩니다. 순서가 지정된 목록 중 하나를 가져옵니다. , 그런 다음 다른 순서 목록의 나머지 요소를 r의 아래 첨자 k에서 아래 첨자 t까지의 셀에 복사합니다. 우리는 병합 정렬 알고리즘을 구현하기 위해 일반적으로 재귀를 사용합니다. 먼저 정렬할 간격 [s, t]를 중간점을 기준으로 2개로 나눈 다음 왼쪽 하위 범위를 정렬한 다음 오른쪽 하위 범위를 정렬합니다. 마지막으로 왼쪽 간격과 오른쪽 간격이 순서가 지정된 간격 [s,t]로 병합됩니다.

# -*- coding: UTF-8 -*-
'''
Created on 2017年9月2日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def merge(left, right):
  i, j = 0, 0
  result = []
  while i < len(left) and j < len(right):
    if left[i] <= right[j]:
      result.append(left[i])
      i += 1
    else:
      result.append(right[j])
      j += 1
  result += left[i:]
  result += right[j:]
  print(result)
  return result
def merge_sort(lists):# 归并排序
  if len(lists) <= 1:
    return lists
  num = int(len(lists) / 2)
  left = merge_sort(lists[:num])
  right = merge_sort(lists[num:])
  return merge(left, right)

프로그램 결과의 예:

8、桶排序/基数排序(Radix Sort)

优点：快，效率最好能达到O(1)
缺点：

1.首先是空间复杂度比较高，需要的额外开销大。排序有两个数组的空间开销，一个存放待排序数组，一个就是所谓的桶，比如待排序值是从0到m-1，那就需要m个桶，这个桶数组就要至少m个空间。

2.其次待排序的元素都要在一定的范围内等等。

算法思想：

是将阵列分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递回方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的阵列内的数值是均匀分配的时候，桶排序使用线性时间（Θ（n））。但桶排序并不是 比较排序，他不受到 O(n log n) 下限的影响。
简单来说，就是把数据分组，放在一个个的桶中，然后对每个桶里面的在进行排序。
例如要对大小为[1..1000]范围内的n个整数A[1..n]排序

首先，可以把桶大小设为10，这样就有100个桶了，具体而言，设集合B[1]存储[1..10]的整数，集合B[2]存储 (10..20]的整数，……集合B[i]存储( (i-1)*10, i*10]的整数，i = 1,2,..100。总共有 100个桶。

然后，对A[1..n]从头到尾扫描一遍，把每个A[i]放入对应的桶B[j]中。 再对这100个桶中每个桶里的数字排序，这时可用冒泡，选择，乃至快排，一般来说任 何排序法都可以。

最后，依次输出每个桶里面的数字，且每个桶中的数字从小到大输出，这 样就得到所有数字排好序的一个序列了。

假设有n个数字，有m个桶，如果数字是平均分布的，则每个桶里面平均有n/m个数字。如果

对每个桶中的数字采用快速排序，那么整个算法的复杂度是

O(n + m * n/m*log(n/m)) = O(n + nlogn - nlogm)

从上式看出，当m接近n的时候，桶排序复杂度接近O(n)

当然，以上复杂度的计算是基于输入的n个数字是平均分布这个假设的。这个假设是很强的 ，实际应用中效果并没有这么好。如果所有的数字都落在同一个桶中，那就退化成一般的排序了。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年9月2日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
import math
lst = [65,56,9,23,84,34,8,6,9,54,11]
#因为列表数据范围在100以内，所以将使用十个桶来进行排序
def radix_sort(lists, radix=10):
  k = int(math.ceil(math.log(max(lists), radix)))
  bucket = [[] for i in range(radix)]
  for i in range(1, k+1):
    for j in lists:
      gg = int(j/(radix**(i-1))) % (radix**i)
      bucket[gg].append(j)
    del lists[:]
    for z in bucket:
      lists += z
      del z[:]
      print(lists)
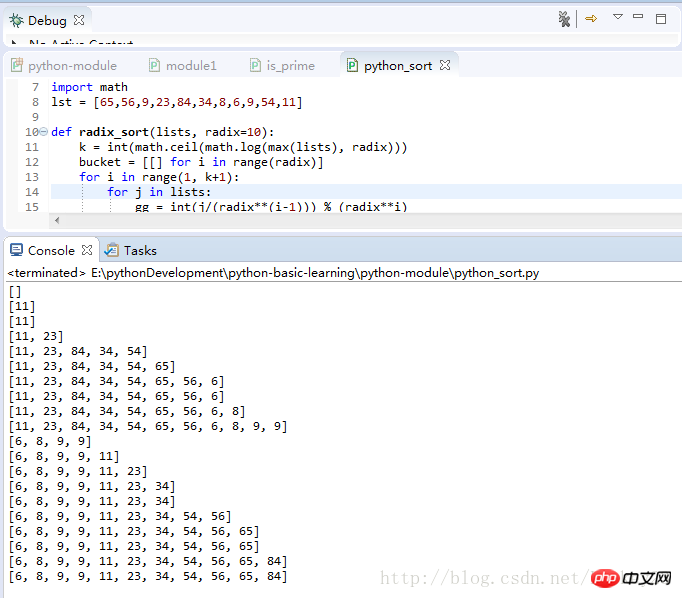
  return lists

程序运行测试结果：

위 내용은 Python의 8가지 정렬 알고리즘 요약(2부)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!