역추적 방법 하위 집합 트리 템플릿을 기반으로 Python의 8-queen 문제 해결

'''
8皇后问题
'''
n = 8 
x = [] # 一个解（n元数组）
X = [] # 一组解
# 冲突检测：判断 x[k] 是否与前 x[0~k-1] 冲突
def conflict(k):
 global x
 for i in range(k):        # 遍历前 x[0~k-1]
  if x[i]==x[k] or abs(x[i]-x[k])==abs(i-k): # 判断是否与 x[k] 冲突
   return True
 return False
# 套用子集树模板
def queens(k): # 到达第k行
 global n, x, X
 if k >= n:   # 超出最底行
  #print(x)
  X.append(x[:]) # 保存（一个解），注意x[:]
 else:
  for i in range(n): # 遍历第 0~n-1 列（即n个状态）
   x.append(i)  # 皇后置于第i列，入栈
   if not conflict(k): # 剪枝
    queens(k+1)
   x.pop()   # 回溯，出栈
# 解的可视化（根据一个解x，复原棋盘。'X'表示皇后）
def show(x):
 global n
 for i in range(n):
  print('. ' * (x[i]) + 'X ' + '. '*(n-x[i]-1))
# 测试
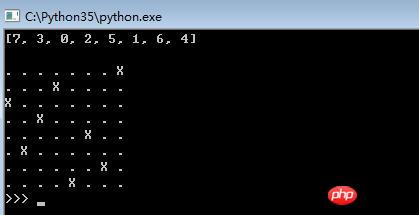
queens(0) # 从第0行开始
print(X[-1], '\n')
show(X[-1])