부분 집합 합 문제의 자세한 예

참고: "하위 집합 및 문제"에 대한 연구가 충분히 심층적이지 않기 때문에 이 문서에는 동적 프로그래밍 재귀 공식을 설명하는 데 불분명한 설명이나 오류가 있을 수 있습니다. 발견하면 알려주시기 바랍니다.

　 부분 집합 합 문제는 다음과 같이 설명할 수 있습니다. n 양의 정수 W=(w₁, w₂, …, w_n) 및 양의 정수 M , ∑wi=M,i∈I[1]과 같은 a 하위 집합 I^{⊆{1, 2, 3, ..., n},}을 찾아야 합니다. 부분 집합 합 문제에 대한 대중적인 설명을 제공하는 예를 들어보겠습니다. 집합 W=(1, 2, 3, 4, 5), 주어진 양의 정수 M=5, 존재합니까 W 의 하위 집합 I. 하위 집합 I에 있는 요소의 합은 M과 같습니다. 이 예에는 분명히 하위 집합 I=(2, 3).

　문제 정의: 양의 정수 집합 S=(w1, w2, w3, …, wn), 주어진 양의 정수 W, s[i, j] i은 S의 하위 집합을 나타내고, j은 하위 집합 i의 합을 나타냅니다. S의 특정 집합 i의 요소 합 j=M이면 문제에 해결책이 있습니다.

　예: S=(7, 34, 4, 12, 5, 3), W=6, S의 하위 집합이 있습니까? 해당 요소의 합은 같습니다. W으로.

이 문제에 대한 해결책도 많이 있습니다. 이 기사에서는 이를 해결하기 위해 동적 프로그래밍 아이디어를 사용하므로 재귀 공식을 도출해야 합니다. 우리는 계속해서 집합 S을 작은 집합으로 나눕니다. 이것이 동적 프로그래밍의 첫 번째 단계: 하위 문제 정의입니다. 집합 S의 가장 작은 집합은 물론 빈 집합이 존재하지 않으며 해당 요소의 합은 j=0과 같습니다. 빈 세트는 자격이 있습니다.

　이 테이블의 열은 집합에 있는 요소의 합을 나타내며, 최대 W 요소에만 도달할 수 있습니다. 물론 W보다 크면 의미가 없습니다. 1이 j=6 열에 나타나면 문제에 대한 해결책을 얻을 수 있습니다. 행은 첫 번째 i(i 포함) 요소로 구성된 하위 집합을 나타냅니다(이 문장은 약간 의심스러울 수 있습니다. 모든 상황을 스캔하는 것이 가능하지 않을까요? 그런 다음 계속 읽으세요). i=0은 빈 집합을 의미합니다.

j=6일 때 빈 집합 상황은 true이라고 정의합니다. 그런 다음 j=0이면 이는 모든 하위 집합 합계에 해당됩니다(빈 집합이 해당 하위 집합임). 따라서 양식은 아래와 같이 계속 채워집니다.

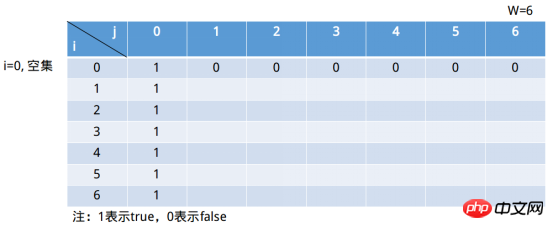
　이것은 실제로 동적 프로그래밍의 세 번째 단계인 초기 상태 정의입니다. 상태 계획의 두 번째 단계는 상태 전환 규칙, 즉 상태 간의 순환 관계를 정의하는 것입니다. s[i, j]의

　 i은 첫 번째 i하위 집합 (에는 i 포함)을 나타냅니다. 실제로 여기서는 이를 두 부분으로 나눕니다.

i번째 요소의 첫 번째 i 하위 집합, 즉 s[i - 1, j]을 제외합니다. ;

i번째 요소의 첫 번째 i 하위 집합을 포함합니다. 　첫 번째
1) 상황의 경우 첫 번째 i - 1 집합 요소의 합은 j과 같고, 첫 번째 에 대한 하위 집합 요소가 있습니다. i 합계는 j과 같습니다.

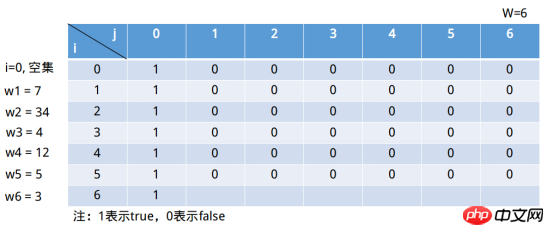
　이해하기 어려운 것은 2)상황입니다. 두 번째 경우에 대해 명확하게 알 수 있는 한 가지는 i in s[i, 수학에서 "특수 값 방법"을 사용하는 경우(예: (3, 34, 9) 집합) 요소의 합이 과 같은 하위 집합이 있습니까? 37, 이때 i=2(하위 집합은 (3, 34)), j = 37, 이때 "에는 첫 번째 이 포함됩니다. i isubset"의 경우, s[2, 37] => s[2, 37 - 34] = s[2, 3], 하위 집합 (3 , 34)물론 요소의 합이 3인 부분 집합도 있습니다. 그렇다면 j = 36, s[2, 36] => s[2, 36 - 34] = s[2, 2], 부분 집합 (3, 34) 요소의 합이 2인 부분 집합은 없습니다. j = 1, s[2, 1] => s[2, 1 - 34] = s[2, -32], j - wi < , 현재 s[2, 1] => s[2 - 1, 1] = s[1, 1], 하위 집합 (3)은 분명히 하위 집합 요소 중에 존재하지 않습니다. 합계는 1과 같습니다. 　 요약하면 재귀 수식은 다음과 같습니다. 　 이 알고리즘을 코드에 구현하기 전에 먼저 재귀 수식을 통해 위의 행렬을 채워야 합니다. 　①i = 1, 이때 부분집합은 (7)

,

j = 1

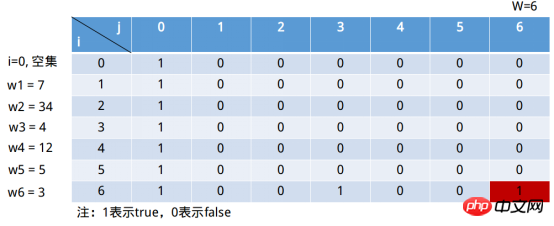
∉(∅), 선택 상황 2) => [0 , 1] || s[1, -6] (i = 0은 빈 집합을 나타냄) 분명히 s[1, 1] = 0입니다.

　②i = 1, 이때 부분집합은 (7), j = 2, j ∉(∅), 선택상황 2) => ] | s[1, -5] (i = 0은 빈 집합을 의미함) 당연히 s[1, 2] = 0입니다.

, 이때 부분집합은 (7), j = 6, j ∉(∅), 선택 상황 2) => ; s[0, 6] || s[1, -1] (i = 0은 빈 집합을 나타냄) 분명히 s[1, 6] = 0입니다.

이때 하위 집합은 (7, 34, 4, 12, 5, 3), j = 1, j ∉ (7, 34, 4, 12, 5), 선택 상황 2) => 1] ​​|| s[6, -2] (i = 0은 빈 집합을 나타냄) 당연히 s[6, 1] = 0입니다. 　②i = 6,

(7, 34, 4, 12, 5, 3), j = 2, j ∉ (7, 34, 4, 12 , 5), 선택 상황 2) => s[5, 1] ​​​​|| s[6, -1] (i = 0은 빈 집합을 의미함) 당연히 s[6, 2] = 0입니다. 　 ③i = 6,

(7, 34, 4, 12, 5, 3), j = 3, j ∉ (7, 34, 4, 12 , 5), 선택 사례 2) => s[5, 1] ​​​​|| 당연히 s[6, 3] = 1입니다. 　...

　⑥i = 6,

(7, 34, 4, 12, 5, 3), j = 6, j ∉ (7, 34, 4, 12 , 5), 선택 상황 2) => s[5, 6] || s[6, 3]. 당연히 s[6, 6] = 1입니다.

　Java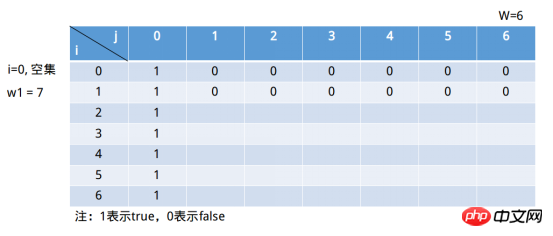

 1 package com.algorithm.dynamicprogramming; 2  3 import java.util.Arrays; 4  5 /** 6  * 子集和问题 7  * Created by yulinfeng on 7/2/17. 8  */ 9 public class SubsetSumProblem {10 11     public static void main(String[] srgs) {12         int[] sets = {7, 34, 4, 12, 5, 3};13         int sum = 87;14         boolean isExistSubSet = subsetSumProblem(sets, sum);15         System.out.println("集合" + Arrays.toString(sets) + "是否存在子集的和等于" + sum + ":" + isExistSubSet);16     }17 18     private static boolean subsetSumProblem(int[] sets, int sum) {19         int row = sets.length + 1;20         int col = sum + 1;21         int[][] solutionMatrix = new int[row][col];22         solutionMatrix[0][0] = 1;23 24         /**25          *    0 1 2 3 4 5 626          * 0 |1|0|0|0|0|0|0|27          * 1 |x|x|x|x|x|x|x|28          * 2 |x|x|x|x|x|x|x|29          * 3 |x|x|x|x|x|x|x|30          * 3 |x|x|x|x|x|x|x|31          * 4 |x|x|x|x|x|x|x|32          * 5 |x|x|x|x|x|x|x|33          * 6 |x|x|x|x|x|x|x|34          */35         for (int i = 1; i < col; i++) {36             solutionMatrix[0][i] = 0;37         }38         /**39          * 初始状态40          *    0 1 2 3 4 5 641          * 0 |1|0|0|0|0|0|0|42          * 1 |1|0|x|x|x|x|x|43          * 2 |x|x|x|x|x|x|x|44          * 3 |x|x|x|x|x|x|x|45          * 3 |x|x|x|x|x|x|x|46          * 4 |x|x|x|x|x|x|x|47          * 5 |x|x|x|x|x|x|x|48          * 6 |1|0|0|x|x|x|x|49          * [i][0] = 1，按行填充50          */51         for (int i = 1; i < row; i++) {52             solutionMatrix[i][0] = 1;53             for (int j = 1; j < col; j++) {54                 solutionMatrix[i][j] = solutionMatrix[i - 1][j];55 56                 if (solutionMatrix[i][j] == 1) {57                     solutionMatrix[i][j] = solutionMatrix[i][j];58                 } else if ( j - sets[i - 1] >= 0 && solutionMatrix[i][j - sets[i - 1]] == 1) {59                     solutionMatrix[i][j] = solutionMatrix[i][j - sets[i - 1]];60                 } else {61                     solutionMatrix[i][j] = 0;62                 }63 64                 if (j == col - 1 && solutionMatrix[i][j] == 1) {65                     return true;66                 }67             }68         }69 70         return false;71     }72 }

　　Python3

 1 def subset_sum_problem(sets, sum): 2     row = len(sets) + 1 3     col = sum + 1 4     solutionMatrix = [[0 for col in range(col)] for row in range(row)] 5     solutionMatrix[0][0] = 1 6     for i in range(1, col): 7         solutionMatrix[0][i] = 0 8  9     for j in range(1, row):10         solutionMatrix[j][0] = 111         for k in range(1, col):12             solutionMatrix[j][k] = solutionMatrix[j - 1][k]13             if solutionMatrix[j][k] == 1:14                 solutionMatrix[j][k] = solutionMatrix[j][k]15             elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):16                 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]17             else:18                 solutionMatrix[j][k] = 019             if k == col - 1 and solutionMatrix[j][k] == 1:20                 return True21 22     return False23 24 sets = [7, 34, 4, 12, 5, 3]25 num = 626 is_exist = subset_sum_problem(sets, num)27 print(is_exist)

위 내용은 부분 집합 합 문제의 자세한 예의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!