JavaScript_javascript 기술의 알고리즘 코드 정렬-JS 튜토리얼-php.cn

집

웹 프론트엔드

JS 튜토리얼

JavaScript_javascript 기술의 알고리즘 코드 정렬

WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB

May 16, 2016 pm 06:10 PM

정렬 알고리즘

정렬의 기초로 사용되는 데이터 항목을 "정렬 코드"라고 하며, 이는 데이터 항목의 키 코드입니다. 검색을 용이하게 하기 위해 일반적으로 컴퓨터의 데이터 테이블이 키 코드별로 정렬되어 있기를 바랍니다. 예를 들어, 정렬된 목록의 절반 검색은 검색 효율성이 더 높습니다. 또한 이진 정렬 트리, B-트리 및 B-트리의 구성 프로세스는 정렬 프로세스입니다. 키가 기본 키인 경우 정렬할 시퀀스에 대해 정렬 후 얻은 결과는 고유합니다. 키가 보조 키인 경우 정렬 결과는 동일한 키를 가진 데이터 요소가 고유하지 않을 수 있습니다. 정렬 결과에서는 이러한 요소 간의 위치 관계가 정렬 전과 같이 유지될 수 없습니다.
데이터 요소의 순서에 대해 특정 정렬 방법을 사용하면 키를 기준으로 정렬됩니다. 정렬 전후에 동일한 키를 가진 요소 간의 위치 관계가 일관되면 이 정렬 방법이 안정적이라고 합니다. 일관성을 유지할 수 없는 정렬 방법을 불안정하다고 합니다.
정렬은 내부 정렬과 외부 정렬의 두 가지 범주로 나뉩니다.
내부 정렬: 정렬할 열을 메모리에 완전히 저장하는 정렬 프로세스를 말하며, 너무 크지 않은 요소 순서에 적합합니다.
외부 정렬: 정렬 프로세스 중에 외부 메모리에 액세스해야 함을 의미합니다. 충분히 큰 요소 시퀀스를 메모리에 완전히 넣을 수 없기 때문에 외부 정렬만 사용할 수 있습니다.

이제 3가지 정렬 알고리즘의 JavaScript 구현을 게시하세요.

첫 번째는 가장 간단한 방법으로 누구나 다 아는 버블정렬입니다. 별로 할말 없고 그냥 코드 붙여넣기

코드 복사 코드는 다음과 같습니다.

/** @name 버블 정렬 
* @lastmodify 2010/07/13 
* @desc 비교 정렬 
복잡도는 O(n*n) 
*/ 
function BubbleSort(list){ 
var len = list.length 
var cl,temp 
while(len--){ 
cl; = list.length ; 
while(cl--){ 
if(list[cl]>list[len] && cl < len){ 
temp = list[len]; 목록[len] = 목록[cl]; 
목록[cl] = 임시 
} 
} 
목록 반환 
} 

 >그럼 마지막 공통 퀵정렬은 기본적으로 면접에서 물어봅니다. 

코드 복사 코드는 다음과 같습니다. /**@name 빠른 정렬

* @lastmodify 2010/07/14

* @desc 비교 정렬 
 최악의 실행 시간 O(n*n) 
 최고 실행 시간 O(nlogn) 
*/ 
function QuickSort(list){ 
var i = 0; 
var j = list.length; 
var len = j 
var left; k = findK (i , j); 
if(k != 0){ 
var leftArr = [] 
var rightArr = [] 
var midArr = [list[k]] ; 
while(len--) { 
if(len != k){ 
if(list[len] > list[k]){ 
rightArr.push(list[len] ); 
} 
else{ 
leftArr.push(list[len]); 
} 
} 
} 
left = QuickSort(leftArr); = QuickSort( rightArr); 
list = left.concat(midArr).concat(right); 
} 
return list 

function findK(i,j) { 
//기본적으로 중간 위치 찾기 
return Math.floor((i j) / 2) 
} 

 
빠른 정렬의 주요 아이디어는 정렬할 분할 정복 방식 시퀀스를 2개의 블록으로 나누어 정렬의 복잡성을 줄입니다. 재귀를 영리하게 사용하는 것도 퀵 정렬의 미묘함입니다. 이전 예에서는 먼저 findK 함수를 사용하여 "참조 요소"를 찾은 다음 다른 요소를 이 요소와 차례로 비교하고, 그보다 큰 모든 요소를 ​​하나의 세트에 넣고, 그보다 작은 요소를 다른 세트에 넣습니다. . 두 개의 컬렉션을 정렬합니다. 퀵 정렬의 효율성은 주로 findK 함수의 구현과 정렬할 요소의 순서에 따라 달라집니다. 따라서 퀵정렬은 불안정한 정렬 알고리즘입니다. 

그러나 퀵 정렬은 여전히 ​​비교 기반 정렬 알고리즘입니다. 모든 비교 기반 정렬 알고리즘의 한 가지 특징은 아무리 최적화하더라도 집합의 요소 수가 증가함에 따라 요소 집합의 평균 정렬 시간이 항상 증가한다는 것입니다. 비비교 정렬은 이러한 단점을 매우 잘 극복하여 정렬 시간 복잡도를 숫자와 무관하게 안정적인 값으로 만들려고 합니다. 그 대표적인 것 중 하나가 버킷 정렬(Bucket Sorting)이다. 먼저 JavaScript 구현을 살펴보겠습니다. 

코드 복사

코드는 다음과 같습니다.

 
/**@name 버킷 정렬 
* @author lebron 
* @lastmodify 2010/07/15 
* @desc 비비교 정렬 
*/ 
function BucketSort(list) { 
var len = list.length; 
var range = findMax(list) 
var result = [], 
count = []; 
var i,j; 
for (i = 0; i count.push(0)>} 

for ( j = 0; j count[list[j]] 
result.push(0) 
} 
for ( i = 1; i count[i-1] count[i] 
for (j = len - 1; j >= 0; j--) { 
결과[count[list[j]]] = 목록[j] 
count[list[j]]-- 
결과 반환; 🎜>} 

function findMax(list) { 
return MAX; 
} 

 
보시다시피, 버킷 정렬 구현에서 findMax는 여전히 큰 배열의 범위를 결정하기 위해 함수를 사용했지만 여기서는 상수 MAX로 직접 대체되었습니다. 먼저 길이가 MAX인 큰 배열 수를 초기화합니다. 예를 들어 값이 24인 요소가 있으면 count의 24번째 비트가 1로 표시되고 결과 배열의 길이는 1이 됩니다. 그런 다음 개수 배열에서 1로 표시된 요소의 위치와 전체 개수 배열에서 1로 표시된 요소의 위치를 ​​계산합니다. 이때, count 배열의 n번째 요소의 값은 정렬 후의 위치가 되어야 하며, n은 정렬 후 이 위치에 해당하는 값입니다. 따라서 마지막으로 count 배열의 키 값을 하나씩 결과 배열에 매핑합니다. 
버킷 정렬은 요소가 집합에서 n번째로 큰 경우 이전 요소나 다음 요소가 그 요소보다 크거나 작은지 신경 쓰지 않고 n번째 순위를 매겨야 한다는 아이디어를 교묘하게 사용합니다. 비교하기 위해). 분명히 실제 상황에서는 정렬된 집합의 요소 값의 범위가 집합의 요소 수보다 훨씬 클 가능성이 높으므로 이에 상응하는 거대한 공간의 배열을 할당해야 합니다. 따라서 버킷 정렬의 일반적인 시나리오는 외부 정렬입니다. 

관심 있는 학생들은 서로 다른 규모의 순서로 세 가지 종류의 정렬을 수행하는 데 시간이 많이 걸리는 작업을 테스트할 수 있습니다.

본 웹사이트의 성명

본 글의 내용은 네티즌들의 자발적인 기여로 작성되었으며, 저작권은 원저작자에게 있습니다. 본 사이트는 이에 상응하는 법적 책임을 지지 않습니다. 표절이나 침해가 의심되는 콘텐츠를 발견한 경우 admin@php.cn으로 문의하세요.

핫 AI 도구

Undresser.AI Undress

사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover

사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool

무료로 이미지를 벗다

Clothoff.io

AI 옷 제거제

AI Hentai Generator

AI Hentai를 무료로 생성하십시오.

뜨거운 도구

메모장++7.3.1

사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전

중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기

강력한 PHP 통합 개발 환경

드림위버 CS6

시각적 웹 개발 도구

SublimeText3 Mac 버전

신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제

Gmail 이메일의 로그인 입구는 어디에 있나요?

7343

자바 튜토리얼

1627

Cakephp 튜토리얼

1352

라라벨 튜토리얼

1265

PHP 튜토리얼

1214

Related knowledge

Kuaishou 양면 시장의 복잡한 실험 설계 문제 Apr 15, 2023 pm 07:40 PM

1. 문제의 배경 1. 양면시장 실험의 소개 양면시장, 즉 플랫폼은 생산자와 소비자라는 두 명의 참여자를 포함하며, 양측은 서로를 홍보한다. 예를 들어 Kuaishou에는 영상 제작자와 영상 소비자가 있는데, 그 두 아이덴티티는 어느 정도 겹칠 수 있습니다. 쌍방향 실험은 생산자 측과 소비자 측의 그룹을 결합하는 실험 방법입니다. 양자간 실험에는 다음과 같은 장점이 있습니다. (1) 제품 DAU의 변화, 작품을 업로드하는 사람 수 등 두 가지 측면에 대한 새로운 전략의 영향을 동시에 감지할 수 있습니다. 양자간 플랫폼은 종종 교차 네트워크 효과를 갖습니다. 독자가 많을수록 저자는 더 활발해지며, 저자가 더 활동적일수록 더 많은 독자가 팔로우하게 됩니다. (2) 효과 오버플로 및 전송을 감지할 수 있습니다. (3) 작용 메커니즘을 더 잘 이해하도록 도와주세요. AB 실험 자체는 원인과 결과 사이의 관계를 알려줄 수는 없습니다.

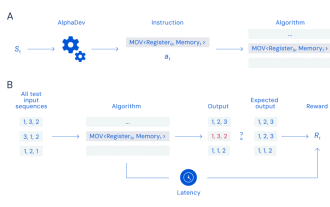구글은 AI를 이용해 10년 순위 알고리즘의 봉인을 깨고 매일 수조 번씩 실행되는데 네티즌들은 이것이 가장 비현실적인 연구라고 말한다. Jun 22, 2023 pm 09:18 PM

정렬 | Nuka-Cola, Chu Xingjuan 기본 컴퓨터 과학 과정을 수강한 친구들은 정렬 알고리즘을 직접 설계했을 것입니다. 즉, 코드를 사용하여 정렬되지 않은 목록의 항목을 오름차순 또는 내림차순으로 재정렬하는 것입니다. 이는 흥미로운 도전이며 이를 수행할 수 있는 방법은 많습니다. 정렬 작업을 보다 효율적으로 수행하는 방법을 찾는 데 많은 시간이 투자되었습니다. 기본 작업으로 정렬 알고리즘은 대부분의 프로그래밍 언어의 표준 라이브러리에 내장되어 있습니다. 대량의 데이터를 온라인으로 정리하기 위해 전 세계의 코드베이스에는 다양한 정렬 기술과 알고리즘이 사용되지만 적어도 LLVM 컴파일러와 함께 사용되는 C++ 라이브러리에 관한 한 정렬 코드는 10년 넘게 변경되지 않았습니다. . 최근 Google DeepMindAI 팀은

Vue 기술 개발에서 데이터를 필터링하고 정렬하는 방법 Oct 09, 2023 pm 01:25 PM

Vue 기술 개발에서 데이터 필터링 및 정렬 방법 Vue 기술 개발에서 데이터 필터링 및 정렬은 매우 일반적이고 중요한 기능입니다. 데이터 필터링 및 정렬을 통해 필요한 정보를 신속하게 쿼리하고 표시할 수 있어 사용자 경험이 향상됩니다. 이 기사에서는 Vue에서 데이터를 필터링하고 정렬하는 방법을 소개하고 독자가 이러한 기능을 더 잘 이해하고 사용할 수 있도록 구체적인 코드 예제를 제공합니다. 1. 데이터 필터링 데이터 필터링이란 특정 조건에 따라 요구 사항을 충족하는 데이터를 필터링하는 것을 의미합니다. Vue에서는 comp를 전달할 수 있습니다.

배열의 정렬 알고리즘은 무엇입니까? Jun 02, 2024 pm 10:33 PM

배열 정렬 알고리즘은 요소를 특정 순서로 정렬하는 데 사용됩니다. 일반적인 유형의 알고리즘은 다음과 같습니다. 버블 정렬: 인접한 요소를 비교하여 위치를 바꿉니다. 선택 정렬: 가장 작은 요소를 찾아 현재 위치로 바꿉니다. 삽입 정렬: 올바른 위치에 요소를 하나씩 삽입합니다. 빠른 정렬: 분할 및 정복 방법, 피벗 요소를 선택하여 배열을 분할합니다. 병합 정렬: 분할 및 정복, 재귀 정렬 및 하위 배열 병합.

Swoole Advanced: 멀티스레딩을 사용하여 고속 정렬 알고리즘을 구현하는 방법 Jun 14, 2023 pm 09:16 PM

Swoole은 PHP 언어를 기반으로 하는 고성능 네트워크 통신 프레임워크로 다중 비동기 IO 모드와 다중 고급 네트워크 프로토콜의 구현을 지원합니다. Swoole을 기반으로 멀티 스레딩 기능을 사용하여 고속 정렬 알고리즘과 같은 효율적인 알고리즘 작업을 구현할 수 있습니다. 고속 정렬 알고리즘(QuickSort)은 벤치마크 요소를 찾아 요소를 두 개의 하위 시퀀스로 나누고 벤치마크 요소보다 크거나 같은 요소를 왼쪽에 배치합니다. 요소는 오른쪽에 배치됩니다. 그런 다음 왼쪽 및 오른쪽 하위 시퀀스가 배치됩니다.

MySQL과 Java를 사용하여 간단한 정렬 알고리즘 기능을 구현하는 방법 Sep 20, 2023 am 09:45 AM

MySQL과 Java를 사용하여 간단한 정렬 알고리즘 기능을 구현하는 방법 소개: 소프트웨어 개발에서 정렬 알고리즘은 가장 기본적이고 일반적으로 사용되는 기능 중 하나입니다. 이 기사에서는 MySQL과 Java를 사용하여 간단한 정렬 알고리즘 기능을 구현하는 방법을 소개하고 구체적인 코드 예제를 제공합니다. 1. 정렬 알고리즘 개요 정렬 알고리즘은 특정 규칙에 따라 데이터 집합을 정렬하는 알고리즘입니다. 일반적으로 사용되는 정렬 알고리즘에는 버블 정렬, 삽입 정렬, 선택 정렬, 퀵 정렬 등이 있습니다. 이 글에서는 버블 정렬을 예로 들어 이를 설명하고 구현해 보겠습니다. 2. 남

C#에서 선택 정렬 알고리즘을 구현하는 방법 Sep 20, 2023 pm 01:33 PM

C#에서 선택 정렬 알고리즘 구현 방법 선택 정렬(SelectionSort)은 간단하고 직관적인 정렬 알고리즘으로, 매번 정렬할 요소 중에서 가장 작은(또는 가장 큰) 요소를 선택하여 마지막에 넣는 것이 기본 아이디어입니다. 정렬된 순서. 모든 요소가 정렬될 때까지 이 과정을 반복합니다. 특정 코드 예제와 함께 C#에서 선택 정렬 알고리즘을 구현하는 방법에 대해 자세히 알아보세요. 선택 정렬 방법 만들기 먼저 선택 정렬을 구현하기 위한 방법을 만들어야 합니다. 이 방법은