사례 연구: 연결된 원 문제

연결된 원 문제는 2차원 평면의 모든 원이 연결되어 있는지 확인하는 문제입니다. 이 문제는 깊이 우선 순회를 사용하여 해결할 수 있습니다. DFS 알고리즘에는 많은 응용 프로그램이 있습니다. 이 섹션에서는 연결된 원 문제를 해결하기 위해 DFS 알고리즘을 적용합니다.

연결된 원 문제에서는 2차원 평면의 모든 원이 연결되어 있는지 확인합니다. 모든 원이 연결되어 있으면 아래 그림 (a)와 같이 채워진 원으로 그려집니다. 그렇지 않으면 아래 그림 (b)와 같이 채워지지 않습니다.

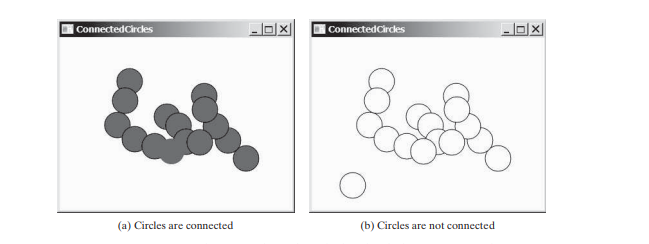
현재 원으로 덮이지 않은 빈 영역에 사용자가 마우스를 클릭하여 원을 만들 수 있는 프로그램을 작성해 보겠습니다. 원이 추가됨에 따라 원이 연결되면 채워지고 그렇지 않으면 채워지지 않게 다시 칠해집니다.

문제를 모델링하기 위한 그래프를 만들어 보겠습니다. 각 원은 그래프의 꼭지점입니다. 두 개의 원이 겹치면 연결됩니다. 그래프에 DFS를 적용하고 깊이 우선 탐색에서 모든 꼭지점을 찾으면 그래프가 연결됩니다.

프로그램은 아래 코드에 나와 있습니다.

JavaFXCircle클래스에는 원의 중심 위치와 반경을 지정하는 데이터 필드x,y및radius가 포함되어 있습니다. 또한 점이 원 안에 있는지 테스트하기 위해contains를 정의합니다.overlaps메서드(76~80행)는 두 원이 겹치는지 확인합니다.

사용자가 기존 원 외부에서 마우스를 클릭하면 마우스 지점을 중심으로 새 원이 생성되고 해당 원이 창(26행)에 추가됩니다.

원이 연결되어 있는지 감지하기 위해 프로그램은 그래프를 구성합니다(46~59행). 원은 그래프의 꼭지점입니다. 가장자리는 49-55행으로 구성됩니다. 두 개의 원 정점이 겹치면 연결됩니다(라인 51). 그래프의 DFS는 트리(라인 60)를 생성합니다. 트리의getNumberOfVerticesFound()는 검색된 정점 수를 반환합니다. 원의 수와 같으면 모든 원이 연결됩니다(61~62행).

위 내용은 사례 연구: 연결된 원 문제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!