이진 트리 선주문 traversal_javascript 기술을 위한 비재귀 알고리즘의 특정 구현-JS 튜토리얼-php.cn

이진 트리 선주문 traversal_javascript 기술을 위한 비재귀 알고리즘의 특정 구현

WBOY

풀어 주다： 2016-05-16 17:04:46

원래의

1650명이 탐색했습니다.

이전 글에서는 이진 트리의 재귀 순회 알고리즘에 대해 이야기했습니다(이진 트리의 루트 우선(선주문) 순회 개선). 이 글에서는 주로 비재귀 순회에 대해 설명합니다. 스택 구조를 사용한 이진 트리 알고리즘

루트 순회를 통해 얻은 비재귀적 알고리즘 아이디어는 다음과 같이 요약됩니다.

1) 스택에 푸시합니다. 주로 헤드 노드를 먼저 스택에 푸시한 후 이 노드를 방문합니다

2) while, 왼쪽 자식에 노드가 없을 때까지 현재 노드를 반복합니다.

3) 노드의 오른쪽 자식이 true이면 1)로 가서 계속 탐색하고, 그렇지 않으면 현재 노드를 종료하고 부모 노드로 가서 1)로 이동합니다.

먼저 이 아이디어에 부합하는 알고리즘을 살펴보겠습니다.

코드 복사 코드는 다음과 같습니다.

int PreOrderTraverseNonRecursiveEx(const BiTree &T, int ( *VisitNode) (TElemType 데이터))
{
if (T == NULL)
{
return -1;
}

BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);

while (!IsStackEmpty(S))
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
} > Pop(&S, (SElemType*)&pBiNode)
}
if (pBiNode->rchild == NULL)
{
Pop(&S, (SElemType*)&pBiNode); // 이때 스택이 비어 있으면 문제가 있는 것입니다
}
pBiNode = pBiNode->rchild;
}

0 반환;
}

참고: 1) 여기서는 스택 구조를 사용합니다. 위의
순차 구조로 저장된 스택

을 참조하세요. 2) 여기에 노드를 저장할 때 노드의 주소인 포인터를 저장하고, 팝핑할 때 포인터를 사용하므로 &pBiNode를 가져오며, pBiNode가 아닙니다. 포인터 사용에 대해 스스로 생각해 보시기 바랍니다. BiTNode *pBiNode로 정의하면 이해하기 쉽습니다.

위 알고리즘은 사실 틀렸습니다! 왜? 여기서 오랫동안 확인했는데, 이 기간 동안 무한 루프가 발생했고, 왼쪽 하위 트리에서 빠져나간 후 오른쪽 하위 트리가 표시되지 않는 경우도 있었습니다. 마지막으로 첫 번째 while 판단 조건을 수정했습니다. Pop 후에 스택이 비어 있지만 오른쪽 하위 트리가 여전히 존재한다면 계속할 수 없습니다. 여기에는 null 포인터가 푸시되지 않으므로 나중에 설명하겠습니다. 푸시를 살펴보세요. 널 포인터의 예는 주로 다음과 같이 왼쪽 하위 트리가 비어 있을 때 스택에 푸시됩니다.

코드 복사

코드는 다음과 같습니다.int PreOrderTraverseNonRecursive(const BiTree &T, int ( *VisitNode) (TElemType 데이터)){ if (T == NULL) {

return -1;

}

BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);
while (!IsStackEmpty(S))

{
GetTop(S, (SElemType*)&pBiNode);
while (pBiNode)
{

VisitNode(pBiNode->data );

pBiNode = pBiNode->lchild;
푸시 (&S, (SElemType)pBiNode) , (SElemType*)&pBiNode);
}
if ( !IsStackEmpty(S))
{
Pop(&S, (SElemType*)&pBiNode);
pBiNode = pBiNode-> rchild;
Push(&S, (SElemType)pBiNode);
}
}

0을 반환합니다.
}

이것은 먼저 루트 노드를 푸시한 다음 왼쪽 하위 트리가 비어 있는지 확인하고, 비어 있지 않으면 스택에 푸시하고, 그렇지 않으면 while 루프를 종료한 후 NULL 노드를 팝합니다. 그런 다음 현재 스택이 비어 있는지 확인하고 비어 있지 않으면 스택을 팝하여 부모 노드를 가져온 다음 오른쪽 자식 노드를 결정하고 오른쪽 자식 노드를 푸시한 다음 오른쪽의 왼쪽 자식인지 확인합니다. 하위 트리가 비어 있고 루프를 계속합니다.

여기에는 두 가지 낭비적인 부분이 있습니다. 하나는 빈 하위 노드를 스택에 푸시하는 것이고, 다른 하나는 GetTop을 자주 사용하여 스택의 최상위 요소를 얻는 것입니다

여기로 돌아가 원래 설계한 알고리즘을 살펴보겠습니다. NULL 포인터나 삽입된 빈 하위 노드가 없지만 여기서는 스택을 판단할 때 추가하는 것을 생각합니다. 현재는 노드가 NULL이면 괜찮으므로 왼쪽 하위 트리 노드가 표시되지 않고 오른쪽 하위 트리 노드가 표시되지 않는 당황 현상이 없습니다.

코드 복사 코드는 다음과 같습니다.

//비재귀적 선주문 순회 이진 트리
int PreOrderTraverseNonRecursiveEx(const BiTree &T,
int (*VisitNode)(TElemType data))
{
if (T == NULL)
{
return - 1;
}

BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);

while ( !IsStackEmpty(S) || pBiNode) //주요 수정은 이 문장입니다
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
}
pBiNode = pBiNode->lchild;
}
if( pBiNode == NULL)
{
Pop(&S, (SElemType*)&pBiNode)
}
if ( pBiNode->rchild == NULL)
{
Pop( &S, (SElemType*)&pBiNode); //이때 스택이 비어 있으면 문제가 있는 것입니다
}
pBiNode = pBiNode->rchild;
}
return 0;
}

첫 번째 while 루프에 이것을 추가하면 테스트 케이스는 이진 트리 선주문 순회와 유사합니다. 다음과 같이 이전 섹션의 이진 트리 예제를 테스트합니다.

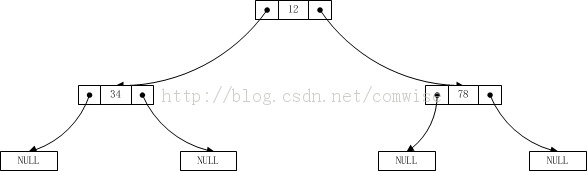
이진 트리 선주문 traversal_javascript 기술을 위한 비재귀 알고리즘의 특정 구현

이때 입력된 데이터는 여전히 12 34 0 0 78 0 0 입니다. 테스트 결과는 다음과 같습니다.

--- BiTree ---
BiTree 노드 데이터를 입력하세요:
12
BiTree 노드 데이터를 입력하세요:
34
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
78
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
0
12 34 78

이것은 테스트하기에 충분하지 않습니다. 다음 이진 트리를 살펴보겠습니다.

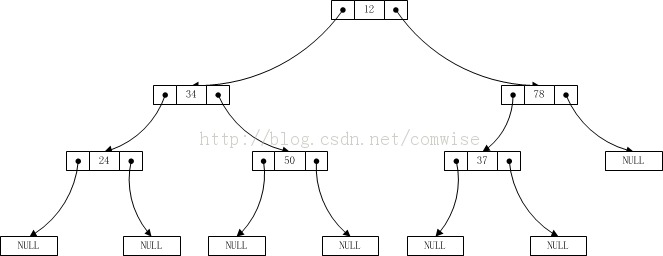
이진 트리 선주문 traversal_javascript 기술을 위한 비재귀 알고리즘의 특정 구현

이때 입력되는 데이터는 12 34 24 0 0 50 0 0 78 37 0 0 0이어야 합니다. 테스트 결과는 다음과 같습니다.

--- BiTree ---
BiTree 노드 데이터를 입력하세요:
12
BiTree 노드 데이터를 입력하세요:
34
BiTree 노드 데이터를 입력하세요:
24
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
50
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
78
BiTree 노드 데이터를 입력하세요:
37
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
0
BiTree 노드 데이터를 입력하세요:
0
12 34 24 50 78 37