筆記試験の問題が出題されましたが、全く分かりませんでした。助けてください。 。 。 。
既知のクラスは次のように定義されています
リーリー入力ノードは次の条件を満たします。
1 ノードの値は 0 より大きい浮動小数点数です。
2 ノードの下位ノード (および下位レベルのノード) の値は null または浮動小数点数である可能性があります。 0 より大きいポイント番号
プログラムの機能は次のとおりです。
1 ツリー構造内のすべての null 値を 0 より大きい浮動小数点数に設定します
2 非葉ノードの値 (つまり、子の数が 0 より大きいノードは、その子と等しいです。値の合計
例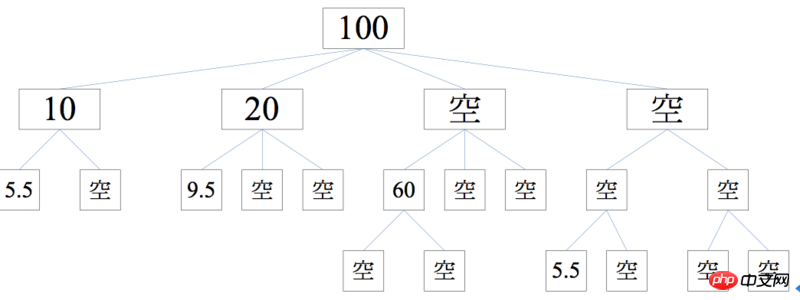
答え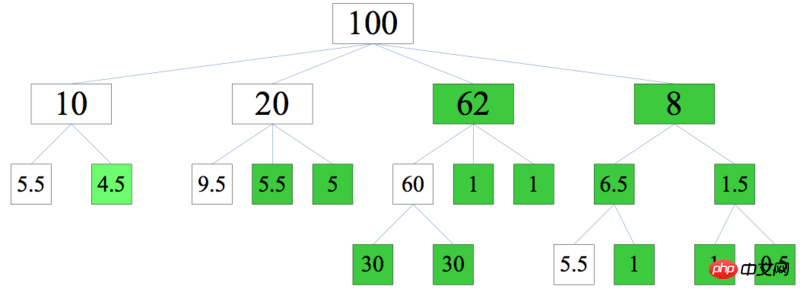
この質問にはどう答えますか?
何人かの専門家がすでに回答しています。以下の 2 人の回答を組み合わせると完璧な答えになります。実際、この答えを採用して均等配分をランダムに変更すると、完璧になります
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
具体的なコードは書いていませんが、考え方をお話します
まず、問題を2つのステップに分けます
Step1.非葉ノードの値を決定します
Step2.葉ノードの値を決定します
処理Step1まず、Step1 が処理された後は、Step2 は必要ありません。親ノードの値に従って均等に分割するだけです。
ステップ 1 の場合、
ステップ 1-1: 各非リーフ ノードを下から上にたどり、その子ノードを合計することで最小値を決定します。たとえば、右端のサブツリーの最小値は 5.5 です。
ステップ 1-2: 上から下に、非リーフ ノードをレイヤーごとに決定します。これは、最初のレイヤーとして [100]、2 番目のレイヤーとして [10、20、?、?] などの名前を付けます。の上。 step1-1の結果より、2層目の最小値は[10, 20, >60, >5.5]となります。その最小値の合計を100から引いて等分します。結果は[10, 20, 62.25, 7.75]です
ステップ1-3: 上記と同様に、3番目の層を決定します。結果は[5.5, 4.5] [9.5, 5.25, 5.25] [60, 1.125, 1.125] [6.625, 1.125]
ここの最後のグループはより特別であり、考慮する必要があります。 7.75 が割り当てられるまでに、左下隅にはすでに 5.5 が存在するため、7.75 で自由に使用できる数値は 7.75-5.5=2.25 を等分します。両側、結果は [6.625, 1.125] です
ステップ 1-4: 最後の層は次のように考えています。くどくど言う必要はありません。実際にはステップ 2 です。均等に分割するだけです。
この質問を読んだところ、とても興味深いと思いました。そこで考えて以下のような質問をしてみました。
私のアイデアは再帰です。
階層的にトラバースし、各レベルで決定された値を合計し、空のノードを親ノードの値から決定された値の合計を引いた値に分割します(質問の要件)。次に、ノードが葉ノードでない場合は、上記の方法に従って再帰します。
しかし、特定のリーフノードなどの各ノードの値を決定する場合、それらの値の一部は親ノードによって制約され、一部は親ノードによって制約されません。 、2 番目の層の 3 番目のノードなど、 の 2 つの葉ノードに割り当てた値がその親ノードを要件を満たさない場合、これは質問の意味を満たしません。したがって、私が望むのは、値が決定されるたびにこれらのノードの値範囲を渡すことです。これらの範囲を決めるといくつかの問題が発生し、問題が複雑になります。
各空ノードの最大値は、親ノードの値から同じ子ノードの値を引いた値である必要があり、最小値は、その子ノードの貴重な要素の合計より大きくなければなりません。 。特定の範囲のみが決定されるため、その葉ノードのいくつかのランダムな値を選択しても、残りのノードが質問の意味を満たさなくなることはありません。一般に、同じ親ノードを持つ各空ノードの値は相互に制約されます。1 つのノードの値はそれ自体を満たしますが、他のノードは要件を満たさなくなります。例:
この方法で値が取得されると、ローカルで満たされることになり、他のノードの値が要件を満たさなくなります。したがって、制約がないと予期しない結果が生じる可能性があります。これらの範囲を決定する必要があります。
要約すると、これらは私が考えた後の単なる考えであり、いくつかの間違いがあるかもしれませんので、修正してください。