
2023年に開催された国際学会AIBT 2023において、Ratidar Technologies LLCは公平性に基づくランキング学習アルゴリズムを公開し、同学会の最優秀論文レポート賞を受賞しました。 Skellam Rank と呼ばれるこのアルゴリズムは、統計原理を最大限に活用し、ペアワイズ ランキングと行列分解テクノロジーを組み合わせて、レコメンデーション システムの精度と公平性の問題を解決します。レコメンダー システムには革新的なランキング学習アルゴリズムがほとんどないため、Schramam のランキング アルゴリズムは非常に優れたパフォーマンスを示し、カンファレンスで研究賞を受賞しました。シュラムのアルゴリズムの基本原理を以下に紹介します:
まずポアソン分布を思い出してください:
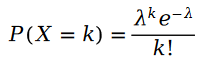
ポアソン分布のパラメーターの計算式は次のとおりです。
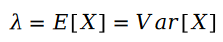
#2 つのポアソン変数の差がシラム分布です。
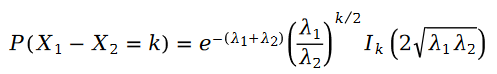
式には次の内容があります:
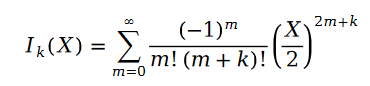
関数が呼び出されます。第 1 種ベッセル関数。
統計学のこれらの基本概念を使用して、Pairwise Rank ランキング学習推奨システムを構築しましょう。
私たちはまず、ユーザーによるアイテムの評価はポアソン分布の概念であると考えています。言い換えると、ユーザーのアイテム評価値は次の確率分布に従います。
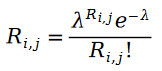
ユーザーがアイテムを評価するプロセスを次のように説明できる理由ポアソン プロセス。ユーザーのアイテム評価にはマシュー効果があるため、つまり、ユーザーの評価が高いほど、より多くの人がそのアイテムを評価するため、アイテムを評価した人の数を使用して、アイテムの評価の分布を近似することができます。アイテムの評価。アイテムを評価する人の数は、どのようなランダムなプロセスに従いますか?当然、ポアソン過程を考えます。ユーザーがアイテムを評価する確率は、何人がそのアイテムを評価したかの確率に似ているため、ポアソン過程を自然に使用して、ユーザーがアイテムを評価するプロセスを近似することができます。
# ポアソン過程のパラメーターをサンプル データの統計量に置き換えて、次の式を取得しましょう。
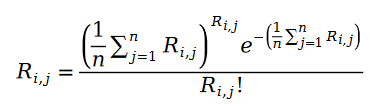
##パリワイズランキングの最尤関数式を以下に定義します。ご存知のとおり、いわゆるペアワイズ ランキングとは、モデルがデータ サンプル内の既知のランキング ペアの関係を最大限に維持できるように、最尤関数を使用してモデル パラメーターを解決することを意味します。
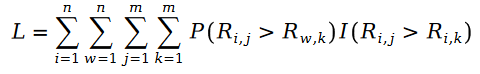 ##式内の R はポアソン分布であるため、両者の差はシラム分布、つまり次のようになります。
##式内の R はポアソン分布であるため、両者の差はシラム分布、つまり次のようになります。
変数 E は次のように定義されます。
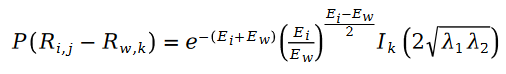
シュラム分布の式を次のように導入します。最尤関数 損失関数 L を計算すると、次の式が得られます。
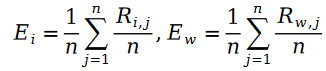
#変数 E に現れるユーザー評価値 R について、それを解決するには行列分解を使用します。行列分解のパラメーター ユーザー特徴ベクトル U とアイテム特徴ベクトル V を解決する変数として使用します:
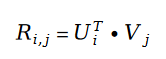
ここでは、まず行列分解の概念を確認します。行列分解の概念は、2010 年頃に提案された推薦システムのアルゴリズムです。このアルゴリズムは、史上最も成功した推薦システムのアルゴリズムの 1 つと言えます。今日に至るまで、多くのレコメンデーション システム会社が行列分解アルゴリズムをオンライン システムのベースラインとして使用しており、人気のある古典的なレコメンデーション アルゴリズム DeepFM の重要なコンポーネントである Factorization Machine も、行列分解アルゴリズムを改良したものです。レコメンデーション システム アルゴリズム バージョンは行列分解と密接に関係しています。行列因数分解アルゴリズムに関する画期的な論文があります。それは、2007 年の確率的行列因数分解です。著者は統計学習モデルを使用して、線形代数における行列因数分解の概念を再モデル化し、行列因数分解に最初の数学的理論的基礎を与えました。時間。
行列分解の基本概念は、ベクトルの内積を使用して、ユーザー評価行列の次元を削減しながら未知のユーザー評価を効率的に予測することです。行列分解の損失関数は次のとおりです。
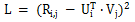
行列分解アルゴリズムには、上海交通大学が提案した SVDFeature など、さまざまなバリエーションがあります。線形モデリングを組み合わせて使用すると、行列分解の問題が特徴量エンジニアリングの問題に変わります。 SVDFeature は、行列因数分解の分野における画期的な論文でもあります。行列分解をペアワイズ ランキングに適用して、未知のユーザー評価を置き換えてモデリングの目的を達成することができます。古典的なアプリケーション ケースには、ベイジアン ペアワイズ ランキングの BPR-MF アルゴリズムが含まれ、シュラマム ランキング アルゴリズムも同じアイデアに基づいています。
シュラマム並べ替えアルゴリズムを解くために確率的勾配降下法を使用します。確率的勾配降下法は、解の目的を達成するために解のプロセス中に損失関数を大幅に単純化できるため、損失関数は次の式になります。
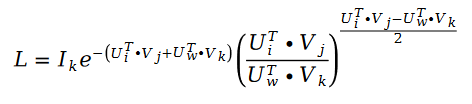
確率的勾配降下法を使用して未知のパラメーター U と V を解くと、次のような反復公式が得られます。
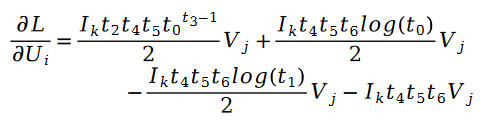
ここで、
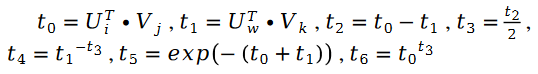
さらに:
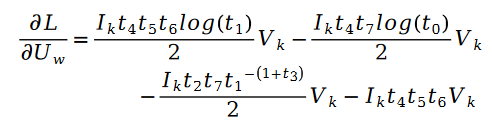
その中に:
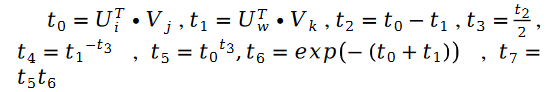
未知のパラメーター変数 V の解も同様で、次の式があります。
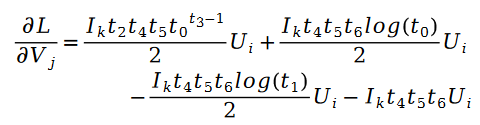
その中に:
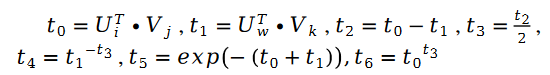
さらに:
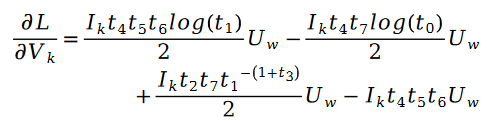
その中に
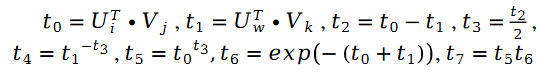
次の疑似コードを使用して、アルゴリズム プロセス全体を示します。

アルゴリズムの有効性を検証するために、論文の著者は MovieLens 100 万データセットと LDOS-CoMoDa データセットに対してテストを実施しました。最初のデータ セットには、6040 人のユーザーと 3706 本の映画の評価が含まれています。評価データ セット全体には約 100 万の評価データが含まれており、推奨システムの分野で最もよく知られている評価データ コレクションの 1 つです。 2 つ目のデータ コレクションはスロベニアからのもので、インターネット上では珍しいシナリオベースのレコメンデーション システム データ コレクションです。データ セットには、121 人のユーザーと 1,232 本の映画からの評価が含まれています。著者は Schram のソートを他の 9 つの推奨システム アルゴリズムと比較しました。主な評価指標は MAE (平均絶対誤差、精度のテストに使用) とマシュー効果度 (主に公平性のテストに使用) です:
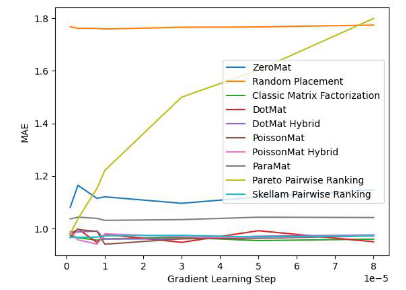
#図 1. MovieLens 100 万のデータセット (MAE インジケーター)
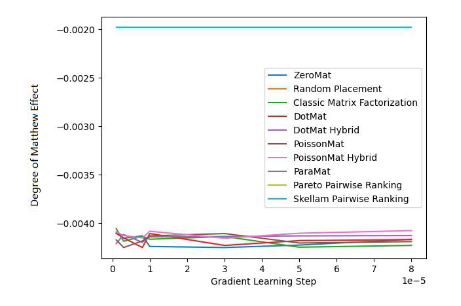
図 1 と図 2 を通じて、Skilam ソートが MAE 指標で良好に機能することがわかりました。しかし、グリッド検索の実験プロセス全体では、パフォーマンスが他のアルゴリズムよりも優れているという保証はありません。しかし、図 2 を見ると、シュラムのソートが他の 9 つの推奨システム アルゴリズムをはるかに上回って、公平性指数において先頭に立っていることがわかります。
LDOS-CoMoDa データ セットに対するこのアルゴリズムのパフォーマンスを見てみましょう:
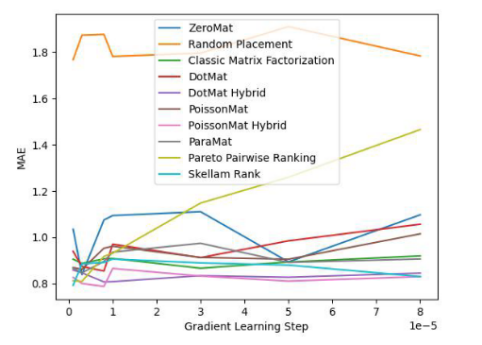
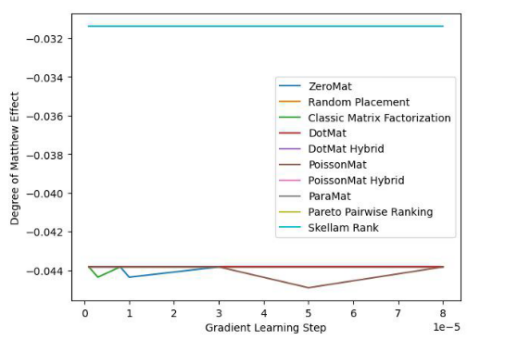 ##図 4. LDOS-CoMoDa データセット (マシュー効果指標)
##図 4. LDOS-CoMoDa データセット (マシュー効果指標)
図 3 と図 4 から、シュラムのソートは公平性指標において比類のないものであり、精度指標において優れたパフォーマンスを示していることがわかります。結論は前の実験と同様です。
シラム ソートは、ポアソン分布、行列分解、ペアワイズ ランキングなどの概念を組み合わせたもので、レコメンデーション システムでは珍しいランキング学習アルゴリズムです。技術分野においては、ランキング学習技術を習得している人はディープラーニングを習得している人の6分の1しかいないため、ランキング学習は希少な技術です。そして、レコメンドシステムの分野で独自のランキング学習を発明できる人材はさらに少ないのです。ランキング学習アルゴリズムは、スコア予測という狭い視点から人々を解放し、最も重要なのはスコアではなく順位であることを人々に認識させます。公平性に基づいたランキング学習は現在、情報検索の分野、特に SIGIR などのトップカンファレンスで非常に人気があり、公平性に基づいた推薦システムに関する論文は非常に歓迎されており、読者の注目を集めることが期待されています。
著者について
以上がシュラムの並べ替え - 公平性に基づいて並べ替えを学習するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。