単純線形回帰は、2 つの連続変数間の関係を調べるために使用される統計手法です。このうち、一方の変数を独立変数(x)、もう一方の変数を従属変数(y)と呼びます。これら 2 つの変数の間に線形関係があると仮定し、独立変数の特性に基づいて従属変数の応答値 (y) を正確に予測する一次関数を見つけようとします。直線を当てはめることで、予測結果を得ることができます。この予測モデルを使用すると、独立変数の変化に応じて従属変数がどのように変化するかを理解し、予測することができます。
この概念を理解するために、各独立変数 (経験年数) に対応する従属変数 (給与) の値を含む給与データ セットを使用できます。
年間給与と経験
1.1 39343.00
1.3 46205.00
1.5 37731.00
2.0 43525.00
2.2 39891.00
2.9 56642.00
3.0 60150.00
3.2 54445.00
3.2 64445.00
3.7 57189.00
一般的な目的のために、
x を特徴ベクトルとして定義します。つまり、x=[x_1,x_2,....,x_n]、
y を次のように定義します。応答ベクトル、つまり、n 個の観測値の y=[y_1,y_2,....,y_n]
(上記の例では、n=10)。
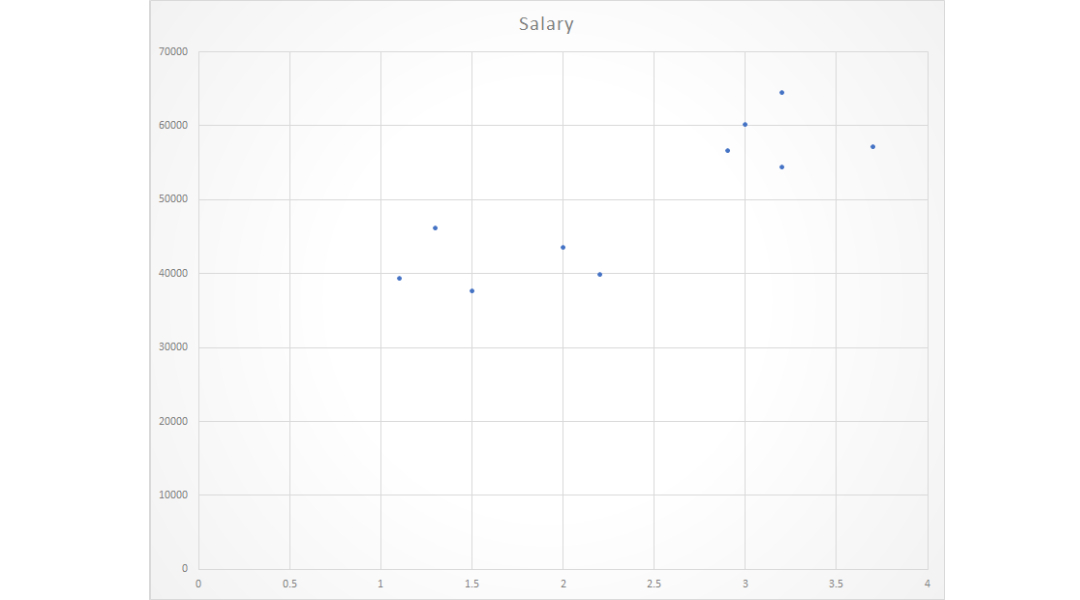
次に、上記の散布図に適合する線を見つける必要があります。任意の y 値または任意の x 値に対する応答を予測します。
最適な直線は回帰直線と呼ばれます。
dataset=read.csv('salary.csv')
install.packages('caTools')
library(caTools)
split=sample.split(dataset$Salary,SplitRatio=0.7)
trainingset=subset(dataset,split==TRUE)
testset=subset(dataset,split==FALSE)
lm.r=lm(formula=Salary~YearsExperience,
data=trainingset)
coef(lm.r)
ypred=predict(lm.r,newdata=testset)
install.packages("ggplot2")
library(ggplot2)
ggplot()+geom_point(aes(x=trainingset$YearsExperience,
y=trainingset$Salary),colour='red')+
geom_line(aes(x=trainingset$YearsExperience,
y=predict(lm.r,newdata=trainingset)),colour='blue')+
ggtitle('Salary vs Experience(Training set)')+
xlab('Years of experience')+
ylab('Salary')
ggplot()+
geom_point(aes(x=testset$YearsExperience,y=testset$Salary),
colour='red')+
geom_line(aes(x=trainingset$YearsExperience,
y=predict(lm.r,newdata=trainingset)),
colour='blue')+
ggtitle('Salary vs Experience(Test set)')+
xlab('Years of experience')+
ylab('Salary')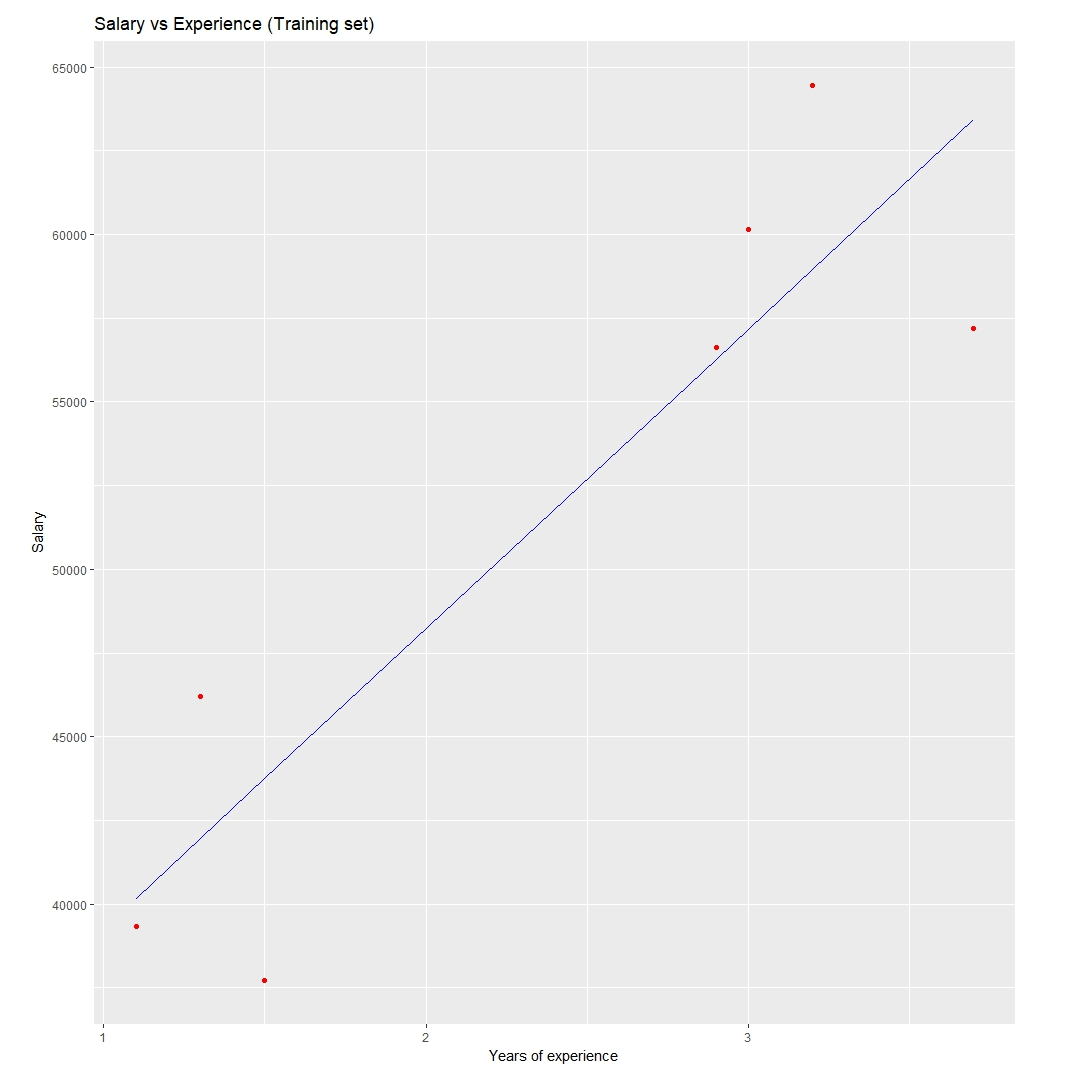
以上がR で単純な線形回帰法を実装し、その概念を説明するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
