
(1)、分析式は整数であり、独立変数は任意の実数にすることができます;
解析式の分数の場合、独立変数はゼロ以外の実数値を取る必要があります。
(3). 解析式が二次根号または偶数根号である場合、独立変数をラジカンドが 0 以上の実数とする必要があります。これにより、分析式が意味を持ち、解決可能であることが保証されます。
(4). 複雑な関数解析式を含む複合関数については、解析式の各要素が意味のあるものであるかどうかを総合的に考慮する必要があります。計算を実行する前に、各関数の定義域と値の範囲を注意深く分析して、複合関数全体の分析式が意味のあるものであることを確認する必要があります。これにより、計算中のエラーや不確実性が回避されます。
y=1/x √(3x-1) のような方程式を解くときは、関数の実際の意味を考慮して、独立変数の値の範囲を決定する必要があります。この方程式の場合、関数が実際的な意味で意味を持つようにするには、その独立変数 x の値の範囲が x ≥ 1/3.2 を満たす必要があります。このようにして、問題をより適切に解決し、適切な結果を得ることができます。
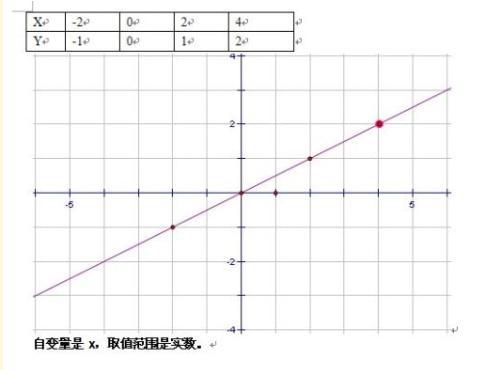
関数変数は整数などの他の変数と似ており、実際の意味はなく、ターゲットを置き換えるためにのみ使用されます。関数変数には、独立変数と従属変数が含まれます。独立変数は、ある値の範囲(定義域)内で任意の値をとる変数であり、従属変数は、独立変数が関数の規則に従って値をとった後に得られる変数です。
詳細情報:
独立変数の値の範囲とは、関数内で意味のあるすべての独立変数の値を指します。数学では、関数の引数の値の範囲を定義して、関数がこの範囲内で意味をなすことを確認します。この範囲は、関数の定義と要件に応じて、実数、整数、有理数、またはその他の特定の数値範囲のセットになります。
独立変数の値の範囲を決定する方法:
まず、分析式が意味のあるものであることを確認するために、独立変数の値の範囲を考慮する必要があります。解析式が整数の場合、独立変数は任意の実数にすることができます。また、解析式が分数形式の場合は、分母がゼロではないことを確認する必要があるため、独立変数の値の範囲は分母が非ゼロになるすべての実数になります。独立変数の値の範囲を合理的に選択することで、分析式の妥当性を保証できます。
解析式に平方根がある場合、有効な解を得るには、ラジカンドが実数ゼロ以上であることを確認する必要があります。実際の問題を表現するために関数分析式が使用される場合、結果の合理性を保証するには、独立変数の値が実際の問題を意味のあるものにしなければなりません。このようにして、これら 2 つの原則に基づいて独立変数の値の範囲を決定し、正しい答えを得ることができます。
独立変数の値の範囲は、無限、有限、または単一 (または複数) の数値にすることができます。関数の解析式に複数の代数式がある場合、関数の独立変数の値の範囲は、各代数式の独立変数の値の範囲の共通部分である必要があります。
関数変数と実際的な問題:
実際的な問題を解決する過程で、変数と定数の概念に遭遇することがよくあります。変数と定数は相対的なことが多く、それらの正体はさまざまな研究プロセスで相互に変換される可能性があります。ただし、実際の問題を扱う場合は、変数と定数の区別に注意する必要があります。変数は変化する可能性がありますが、定数は固定されています。したがって、変数や定数をどのようなタイミングで使用するかはケースバイケースで判断し、謎解きの過程で柔軟に使用する必要があります。
次に、変数間の接続を見つけて、関数を使用してそれらを表現する方法を学びます。このようにして、パズルをよりよく解き、レベルをクリアする方法を見つけることができます。
実際の問題を解決するときは、関数のイメージを使用することが非常に重要です。横軸と縦軸の意味を正しく理解し、関数グラフの性質を理解し、画像を正確に識別して問題を解決できるようにする必要があります。この方法により、関数の特性と動作をより深く理解できるようになり、さまざまな実際的な問題をより効果的に解決できるようになります。
参考:総合事典 - 関数変数
1. コンテンツの概要:
1. 機能に関連する概念:
一般に、特定の変更プロセスには 2 つの変数 x と y が関与します。特定の範囲内の x の特定の値ごとに、対応する一意の y 値が存在する場合、y は x の関数であると言い、x は独立変数と呼ばれます。
関数の意味は次の側面から理解する必要があります:
特定の変化プロセスを研究するとき、2 つの変数間の関数関係を調査します。さまざまな研究プロセスでは、変数と定数が相互に変換される可能性があります。つまり、定数と変数は特定のプロセスに関連しています。相互変換におけるこの柔軟性により、変数間の関係をよりよく理解し、分析できるようになります。
(2) 変数 x の値の範囲は、許可されるすべての値で構成されます。 (3) 変数 x と y の間には明確な対応関係があります。つまり、x の許容値ごとに、それに対応する一意の y 値が存在します。
同じ機能を理解する方法:
関数の概念は、変数 x と変数 y の間に特別な対応 (つまり、対応するルール) があり、変数 x の値の範囲内で、各 x の値が一意の y の値に対応する場合と理解できます。の場合、変数 y は変数 x の関数になります。つまり、関数の概念には次の 2 つの主要な点が含まれます。
(1) y と x の関数関係;(2)関数関係における独立変数xの値の範囲。
これは、同じ関数が上記 2 つの側面、つまり関数関係が同じ (または変形後も同じ) であり、独立変数 x の値の範囲も同じである必要があることを意味します。同じ機能ではありません。関数関係式が同じであるかどうかに気づきやすく、独立変数 x の値の範囲が見落とされやすいことがありますので、この点に注意してください。
以下の関数のうち、y=x と同じ関数関係を持つものは ( ) です。
パズルの解決方法: まず、4 つの関数の解析式を単純化し、それらを y=x と比較して、それらが同じかどうかを確認する必要があります。次に、各関数の独立変数 x の値の範囲を決定し、それを y=x の解析式および独立変数 x の値の範囲と比較する必要があります。両方の条件が満たされる場合にのみ同じ機能です。
解決策: 関数 y=x、その独立変数 x の値の範囲はすべて実数です。
、その独立変数 x の値の範囲はすべて実数 x≥0 です。
、その独立変数 x の値の範囲はすべて実数 x≠0 です。
、その独立変数 x の値の範囲はすべて実数です。
、その独立変数 x の値の範囲はすべて実数です。
明らかに、選択肢 (C) の解析式だけが y=x と同じ値の範囲を持つため、正解は (C) になるはずです。
2. 関数の引数の値の範囲
関数独立変数の値の範囲の原則は次のとおりです:
(1) 解析式は整数であり、独立変数は任意の実数をとることができます。
分析式は分数であるため、独立変数の値を決定するときは、分母がゼロにならないようにする必要があります。これは、分母がゼロであると分数が計算できなくなるためです。有効な解を得るには、解析式の分母がゼロ以外であることを確認してください。
解析式が非合理的な場合には、次の 2 点に注意する必要があります。 1. 二次根号の場合、根号の値は 0 以上である必要があります。したがって、係数がゼロ以上となるような独立変数の値の範囲を見つける必要があります。 2. 3 次根号の場合、独立変数は任意の実数にすることができます。これは、独立変数の値として任意の実数を選択できることを意味します。 これらの考慮事項は、無理数式を正しく解析し、独立変数の値の範囲を決定するのに役立ちます。
上記の形式から分析式を合成する場合、独立変数の値の範囲はそれぞれの条件を同時に満たす必要があります。このようにして、問題をより適切に解決できるようになります。
3. 関数の値
関数値に関連する問題は代数値に変換できます。
4. 機能イメージ
関数グラフィックスは、数値と図形の相互変換を実現します。
以上が関数内の独立変数の値の範囲を決定する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。