
センサー データに基づいてリアルタイムでベクトル化された高精度マップを構築することは、予測や計画などの下流タスクにとって非常に重要であり、効果的に補うことができます。オフラインの高精度マップの場合、マップのリアルタイム パフォーマンスが低いという欠点があります。ディープラーニングの発展に伴い、オンラインでベクトル化された高精度地図構築が徐々に登場し、HDMapNet、MapTRなどの代表的な作品が次々と登場しました。しかし、既存のオンラインでベクトル化された高精度地図構築方法には、地図要素の幾何学的特性 (要素の形状、垂直、平行、その他の幾何学的関係を含む) の調査が不足しています。
ベクトル化された高精度地図は、道路上の要素を高度に抽象化し、各地図要素を 2 次元として表現します。点の並び。都市道路の設計には特定の仕様があります。たとえば、ほとんどの場合、横断歩道は正方形 長方形 または 平行線 であり、分岐や合流を伴わない道路区間では、隣接する 2 つの車線が使用されます。は互いに 平行です。高精度地図のさまざまな要素にも、多くの同様の特性があります。これらの常識的なルールは、地図要素 (長方形、長方形、長方形、平行四辺形、直線など)、またはさまざまなマップ要素 (平行、垂直など) 間の 関連付け 。幾何学的プロパティはマップ要素の表現を強く制約します。オンライン モデル構築の幾何学的プロパティを完全に理解していれば、より正確な結果を得ることができます。 高精度地図のための幾何学的表現の重要性を提案
幾何学的特性の不変性
です。より具体的には、剛体不変性(回転および平行移動変換に対して不変のままである)です。これまでの作業は、単純なポリライン表現を使用する場合でも、制御点を含む多項式曲線 (ベジェ曲線、区分的ベジェ曲線など) を使用する場合でも、絶対座標と絶対座標における基本的なエンドツーエンドの最適化に基づいていました。 絶対座標に基づく最適化目標自体には厳密な不変性がないため、モデルが該当する局所最適解に幾何学的特性の理解が含まれることを期待することは困難です。したがって、幾何学的特性を完全に特徴づけることができ、一定の不変性を有する表現が必要です。 図 1. 幾何学的不変性の例。 車両が右折すると絶対座標が大きく変化します。右側の画像は、対応する現実のシナリオを示しています。

GeMap の設計
#マップ要素の
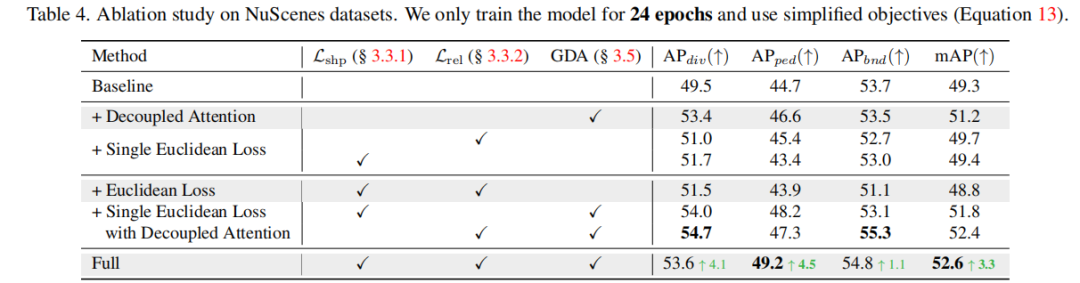
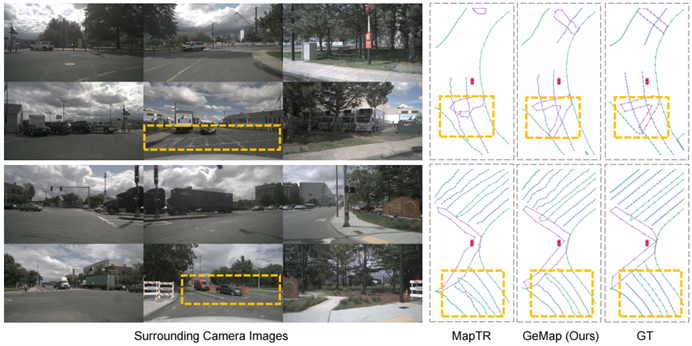
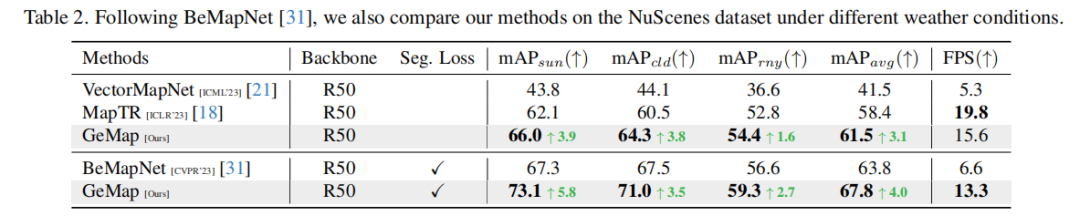
形状を記述できるようにする 長さ と の異なる値を選択しました。オフセット ベクトル間の角度 。これら 2 つ、長さと角度は、私たちが提案する幾何学的表現の基礎を形成します。さらに、形状をより適切に区別して説明し、2 つの異なるタイプの幾何学的特性を関連付けるために、シンプルさの原則に従って設計をさらに洗練しました。 形状を説明するために , we単一の地図要素内の隣接する点間のオフセット ベクトルを計算し、オフセット ベクトルの長さと隣接するオフセット ベクトル間の角度を計算します。この表現は、ポリライン/ポリゴンを一意に識別します。 2 つの画像の例を以下に示します。 幾何学的形状の表現を示す図 2 をご覧ください。 長方形の場合は、直角と 2 組の等しい辺を使用して表現できます。直線の場合は、すべての角度を使用して表現できます。は 0 度または 180 度です。 関連 を特徴付けるために、同様に、まず 任意の 2 点間の距離 を考慮します。ただし、すべてのポイントツーポイント オフセット ベクトルに対して角度を計算すると、表現の複雑さが高くなりすぎて、計算コストが支払えなくなります。具体的には、マップ要素の合計があり、各要素が点で表されると仮定すると、すべての角度のデータ量は (各角度のデータが 32 ビット浮動小数点数であると仮定すると、1000 個とすると、表現は占有スペースが TB レベルに達するだけです)。実際、これは通常の垂直、平行などの関係には必要ありません。したがって、 まず要素内のオフセットを計算し、次に幾何学的表現の一部として 2 つのオフセット間の角度のみを計算します。この簡略化された関連付け表現は、並列関係、垂直関係、その他の関係を記述する機能を保持していますが、対応するデータ量はわずか (前述の条件下で約 4MB) です。理解を容易にするために、いくつかの例も示します。 予測とラベルの幾何学的表現を直接計算し、最適化ターゲットとしてノルムを使用します。 : 幾何学的なデカップリングへの注目 MapTR、PivotNet などで採用されているアーキテクチャです。マップ要素を結合する 上の各点は、Transformer のクエリに対応します。このアーキテクチャの問題は、幾何学的特性の 2 つの主要なカテゴリを区別していないことです。 セルフアテンションでは、すべてのクエリ (つまり、「ポイント」) が相互に平等に作用します。ただし、 マップ要素の形状はクエリのグループに対応します。これらのグループ間の相互作用は、要素の形状を認識する際に問題となります。逆に、要素間の関係を捉える場合には、形状も余分な要素になります。これは、形状の認識と関連性を切り離すことで、より良い結果が得られる可能性があることを意味します 各マップ要素は クエリで構成され、アテンションはクエリ内で実行されます。この 幾何学的形状を処理するためのクエリ 左側は単一要素内で実行される形状アテンション、右側は要素間で実行される関連アテンションです。 nuScenes で 3 セットの実験を実施しました。まず、幾何学的損失とその他の必要な損失 (ポイントツーポイント距離、エッジ方向、分類など) のみを含む目的関数の比較的純粋な組み合わせを使用します。この組み合わせは、提案する幾何学的特性の重要性を強調することを目的としています。 SOTAの結果を追求しすぎず、価値を追求します。結果は、この場合、私たちの方法が MapTR と比較して mAP を改善することを示しています。 GeMap の限界を探るために、セグメンテーションや深度推定などの補助的な目的も追加します。このケースでは、SOTA の結果 (mAP の改善) も達成しました。このような改善を達成するために、推論速度をそれほど犠牲にする必要がないことは注目に値します。最後に、追加の LiDAR モーダル入力の導入も試みました。追加のモーダル入力の助けにより、GeMap のパフォーマンスはさらに向上しました 同様に、Argoverse 2 データ セットでも上記に関して、私たちの方法も非常に優れた結果を達成しました。 書き直された内容は次のとおりです: アブレーション実験 nuScenes でさらに書き直された内容は次のとおりです: アブレーション実験の証明 幾何学的な損失の値そして幾何学的に分離された注意。興味深いことに、予想どおり、幾何学的損失を直接使用すると、モデルのパフォーマンスが低下します。これは、形状と関連付け処理の 構造的結合により、モデルによる幾何学的表現の最適化が困難になるためであると考えられます ; 幾何学的な分離の注意と組み合わせた後、幾何学的損失が本来の役割を果たします (From 「ユークリッド損失」から「フル」まで)。 その他の結果 さらに、nuScenes の視覚的な分析も実行しました。視覚化の結果から、以下の図に示すように、GeMap は回転と平行移動の処理において堅牢であるだけでなく、オクルージョンの問題の解決において一定の利点を示していることがわかります。図 図 5. 視覚的な比較結果では、困難なマップ要素がオレンジ色のボックスでマークされています。 雨の日の実験結果では、オクルージョンの堅牢性も定量的に検証しました(下表参照)。これは、雨が自然にカメラをブロックするためです。 これは、モデルが幾何学的特性を学習するため、オクルージョンがある場合でもマップ要素をより正確に推測できることで説明できます。たとえば、モデルが車線の形状を理解している場合、その一部を「見る」だけで残りを推定できます。モデルは車線の平行関係や車線の幅の特性を理解しているため、たとえそれらの 1 つがブロックされていても、平行関係と幅係数に基づいて、遮蔽された部分を推測することもできます。 我々は、その幾何学的特性を指摘しました。マップ要素とオンラインベクトル化におけるその重要性 高精度マップ構築の価値。これに基づいて、この値を最初に検証するための強力な方法を提案します。さらに、GeMap のオクルージョンに対する堅牢性は、車両と道路の両方が比較的標準化された幾何学的特性を備えているため、他の自動運転タスク (検出、占有予測など) でのオクルージョンに対処するために幾何学的特性を使用するというアイデアを示している可能性があります。もちろん、私たちの手法自体にはさらに研究すべきことがたくさんあります。たとえば、異なる点を使用して、異なる複雑さの幾何学的要素を適応的に記述することができるでしょうか?幾何学的表現を確率論的な観点から理解して、ノイズに対してより堅牢にすることは可能でしょうか?要素の関連付けを単純化したので、幾何学的関連付けをより適切に表現できるものはあるでしょうか?これらはすべて、さらなる最適化のための方向性です。 書き直す必要があるコンテンツは次のとおりです: https://mp.weixin.qq.com/s/BoxlskT68Kjb07mfwQ7Swg link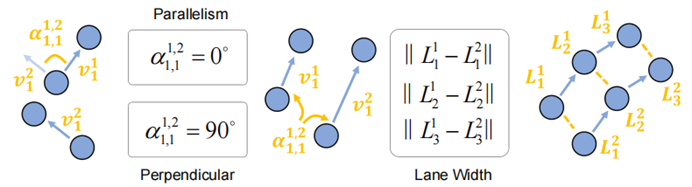
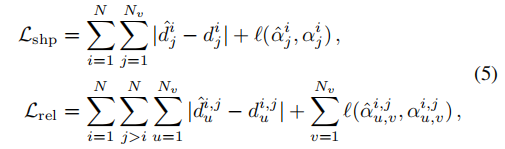
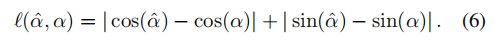
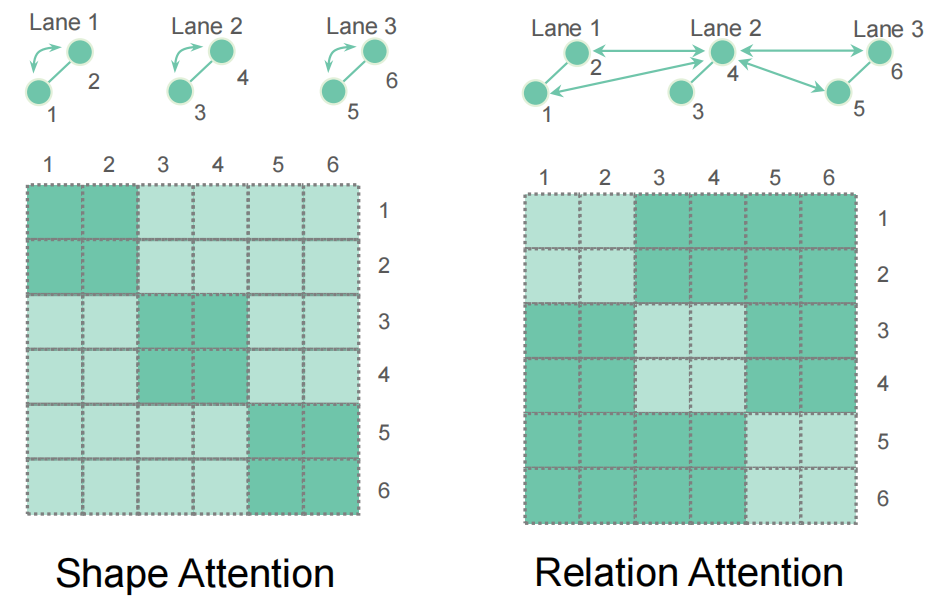
幾何学的関連を処理するために要素間の注意関係を補足します
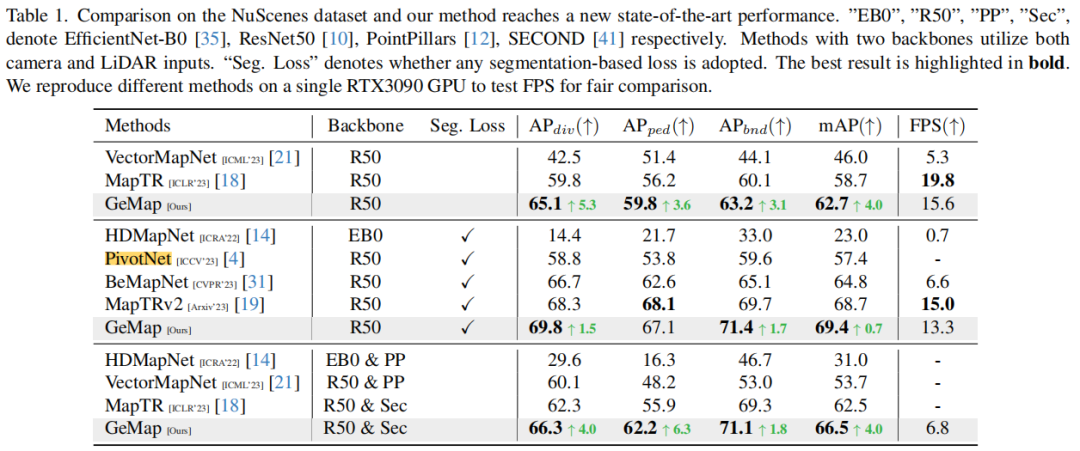
 実験結果
実験結果主な結果

要約

以上が初めてのmAP70%超え! GeMap: ローカル高精度マップ SOTA が再び更新されましたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。