
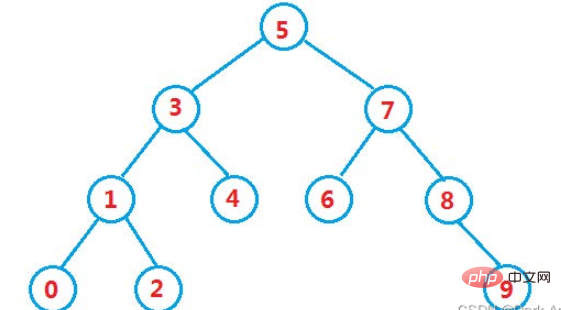
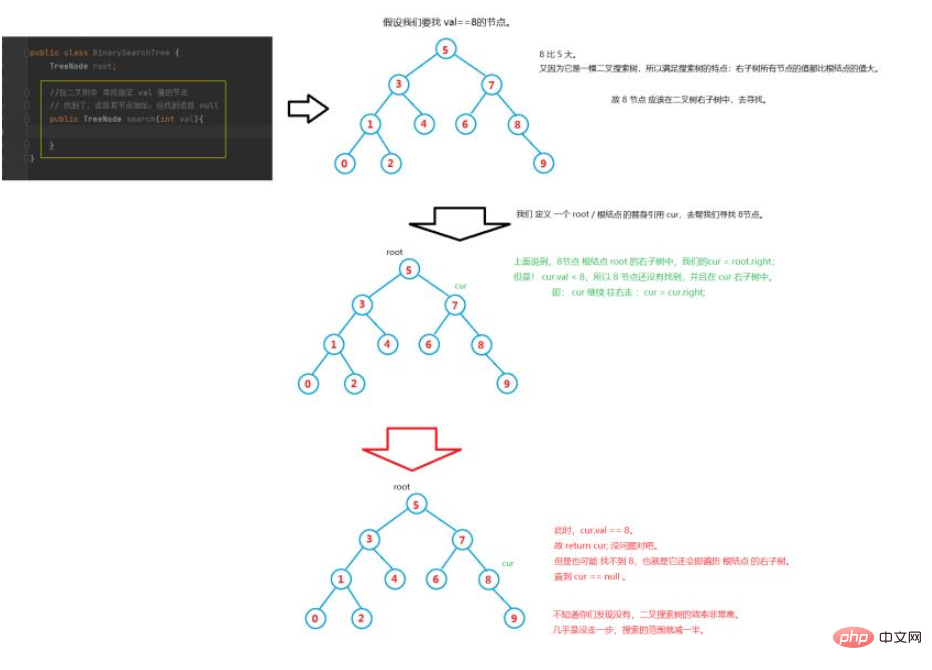
二分探索ツリーは二分ソート ツリーとも呼ばれます。これは空のツリーであるか、または次のプロパティを持ちます。 バイナリ ツリー:
1. 左のサブツリーが空でない場合、左のサブツリー上のすべてのノードの値はルート ノードの値より小さくなります。
2. 右のサブツリーが空でない場合、右のサブツリー上のすべてのノードの値はルート ノードの値より大きくなります。
3. その左側と右側のサブツリーもそれぞれ二分探索ツリーです
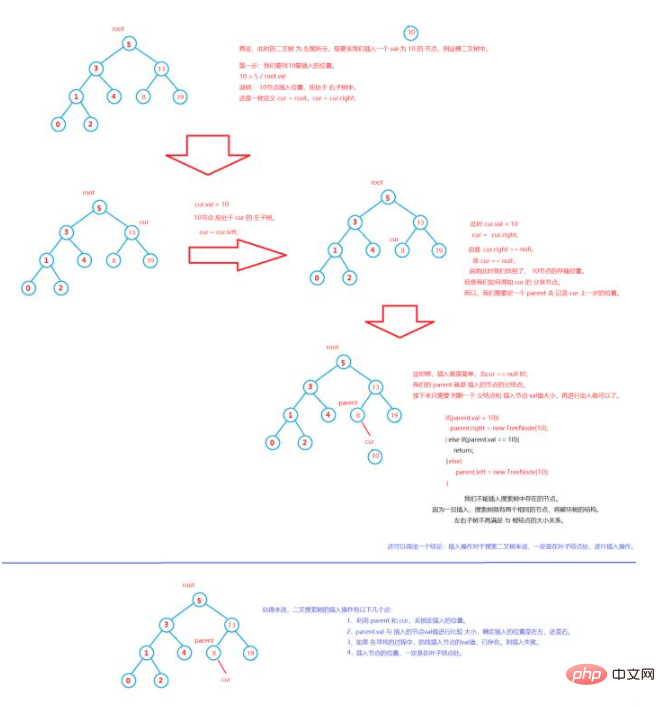
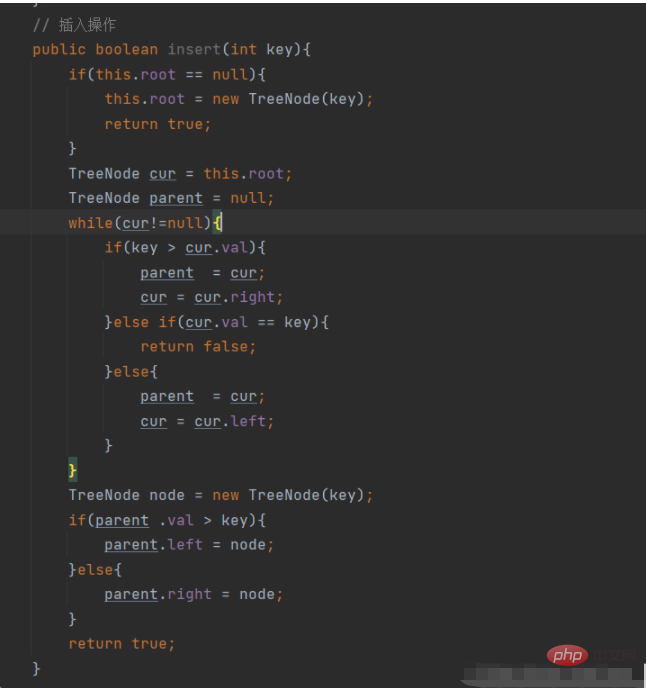
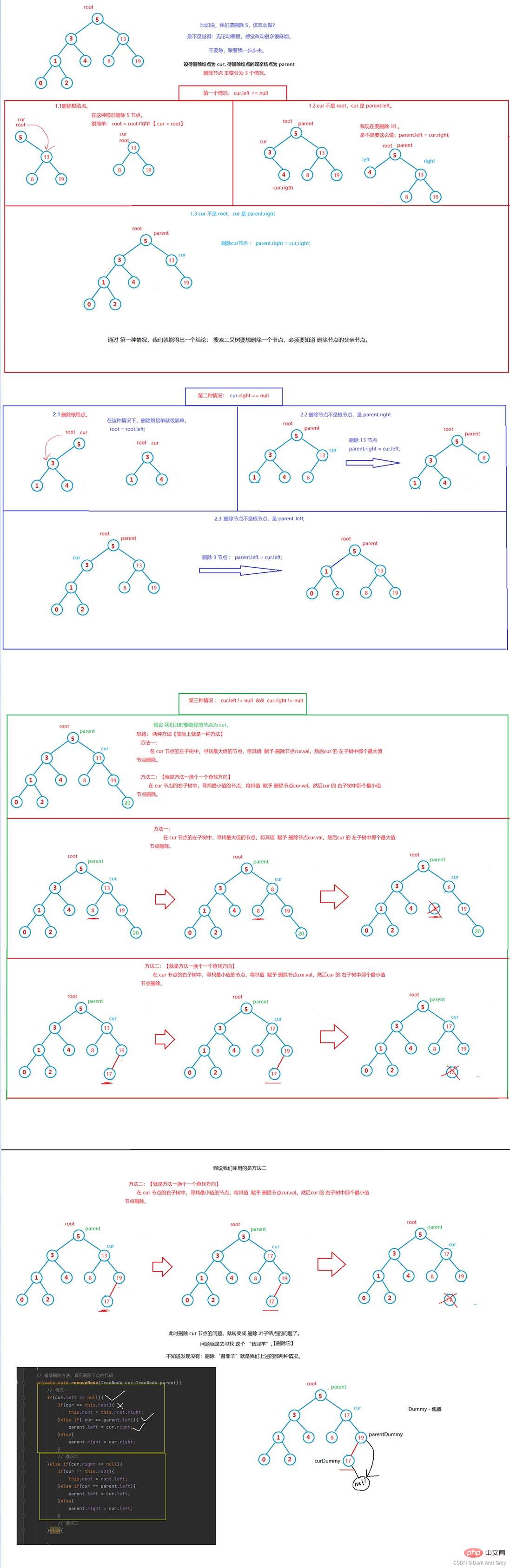
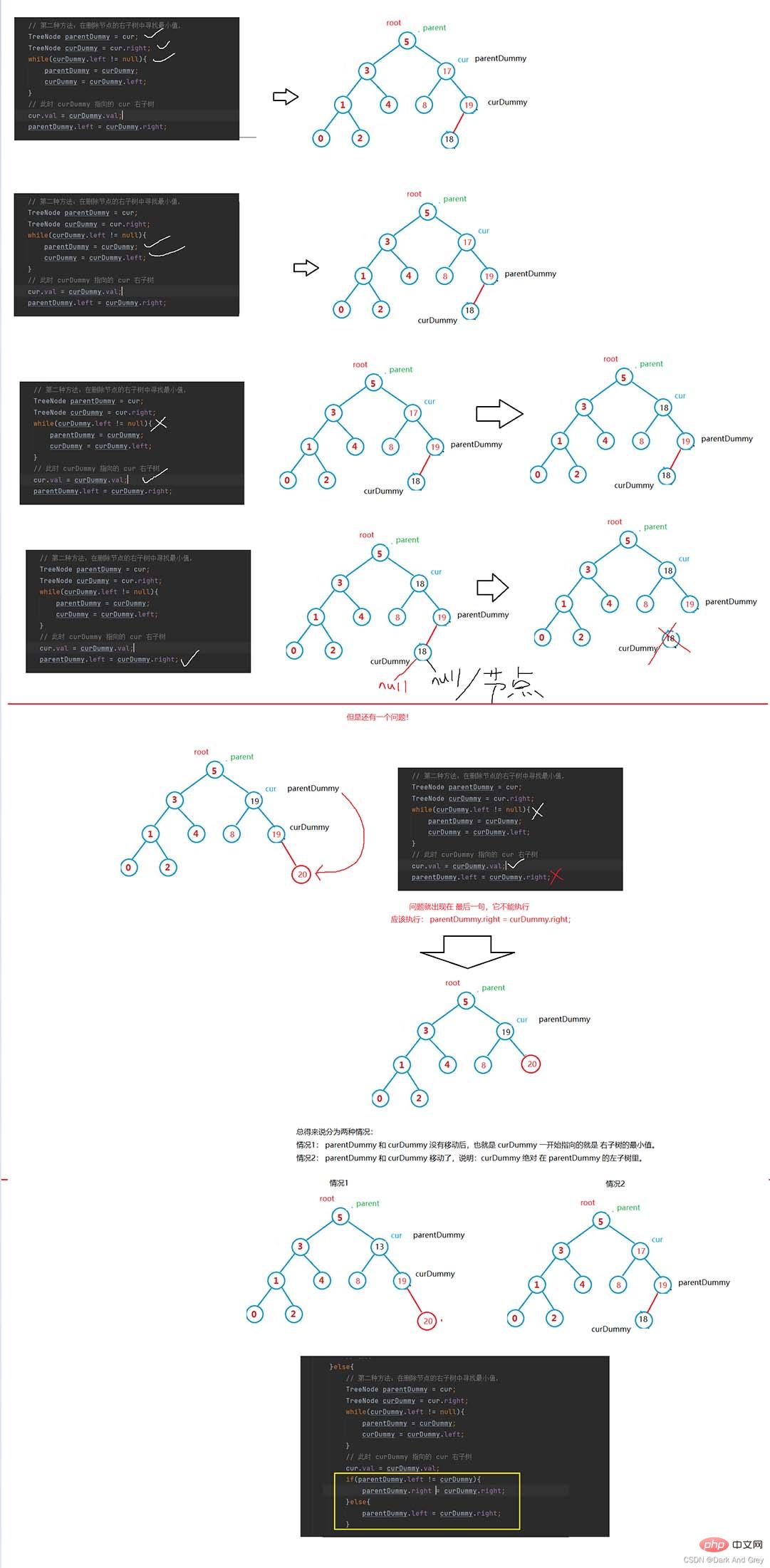 #トータル プログラム - 二分探索ツリーを実装するためのシミュレーション
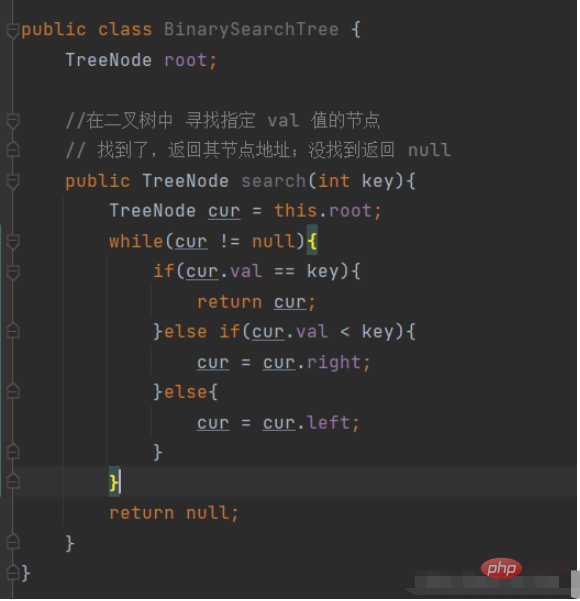
#トータル プログラム - 二分探索ツリーを実装するためのシミュレーション
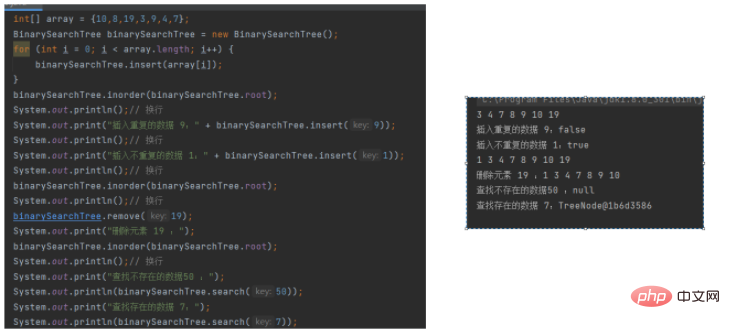
class TreeNode{ public int val; public TreeNode left; public TreeNode right; public TreeNode(int val){ this.val = val; } } public class BinarySearchTree { TreeNode root; //在二叉树中 寻找指定 val 值的节点 // 找到了,返回其节点地址;没找到返回 null public TreeNode search(int key){ TreeNode cur = this.root; while(cur != null){ if(cur.val == key){ return cur; }else if(cur.val < key){ cur = cur.right; }else{ cur = cur.left; } } return null; } // 插入操作 public boolean insert(int key){ if(this.root == null){ this.root = new TreeNode(key); return true; } TreeNode cur = this.root; TreeNode parent = null; while(cur!=null){ if(key > cur.val){ parent = cur; cur = cur.right; }else if(cur.val == key){ return false; }else{ parent = cur; cur = cur.left; } } TreeNode node = new TreeNode(key); if(parent .val > key){ parent.left = node; }else{ parent.right = node; } return true; } // 删除操作 public void remove(int key){ TreeNode cur = root; TreeNode parent = null; // 寻找 删除节点位置。 while(cur!=null){ if(cur.val == key){ removeNode(cur,parent);// 真正删除节点的代码 break; }else if(cur.val < key){ parent = cur; cur = cur.right; }else{ parent = cur; cur = cur.left; } } } // 辅助删除方法:真正删除节点的代码 private void removeNode(TreeNode cur,TreeNode parent){ // 情况一 if(cur.left == null){ if(cur == this.root){ this.root = this.root.right; }else if( cur == parent.left){ parent.left = cur.right; }else{ parent.right = cur.right; } // 情况二 }else if(cur.right == null){ if(cur == this.root){ this.root = root.left; }else if(cur == parent.left){ parent.left = cur.left; }else{ parent.right = cur.left; } // 情况三 }else{ // 第二种方法:在删除节点的右子树中寻找最小值, TreeNode parentDummy = cur; TreeNode curDummy = cur.right; while(curDummy.left != null){ parentDummy = curDummy; curDummy = curDummy.left; } // 此时 curDummy 指向的 cur 右子树 cur.val = curDummy.val; if(parentDummy.left != curDummy){ parentDummy.right = curDummy.right; }else{ parentDummy.left = curDummy.right; } } } // 中序遍历 public void inorder(TreeNode root){ if(root == null){ return; } inorder(root.left); System.out.print(root.val+" "); inorder(root.right); } public static void main(String[] args) { int[] array = {10,8,19,3,9,4,7}; BinarySearchTree binarySearchTree = new BinarySearchTree(); for (int i = 0; i < array.length; i++) { binarySearchTree.insert(array[i]); } binarySearchTree.inorder(binarySearchTree.root); System.out.println();// 换行 System.out.print("插入重复的数据 9:" + binarySearchTree.insert(9)); System.out.println();// 换行 System.out.print("插入不重复的数据 1:" + binarySearchTree.insert(1)); System.out.println();// 换行 binarySearchTree.inorder(binarySearchTree.root); System.out.println();// 换行 binarySearchTree.remove(19); System.out.print("删除元素 19 :"); binarySearchTree.inorder(binarySearchTree.root); System.out.println();// 换行 System.out.print("查找不存在的数据50 :"); System.out.println(binarySearchTree.search(50)); System.out.print("查找存在的数据 7:"); System.out.println(binarySearchTree.search(7)); } }
 パフォーマンス分析
パフォーマンス分析
n 個のノードを持つ二分探索木の場合、各要素の検索確率が等しい場合、二分探索木の平均検索長は二分探索のノード数になります。ツリー 深さの関数。つまり、ノードが深くなるほど、より多くの比較が必要になります。この時点で、さらなる回転を避けるために赤黒ツリーが生成されます。
ただし、同じキー コード セットでも、キー コードが異なる順序で挿入されると、異なる構造の二分探索木が取得される可能性があります。
二分探索木の左右のサブツリー間の高さの差が 1 を超えないことが保証できれば。ハイバランス条件を満たすようにしてください。これは AVL ツリー (高バランス二分探索ツリー) になります。 AVL ツリーには、頻繁なローテーションが必要になるという欠点もあります。効率の無駄が多い。
Java クラス セットとの関係
以上がJavaバイナリサーチツリーの分析例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。