Java 言語を使用してバブル ソートおよび選択ソート アルゴリズムを実装する

バブルソート法 バブルアルゴリズムは、従来のC言語の教科書でよく取り上げられる、比較的安定したソートアルゴリズムです。このソート アルゴリズムを使用する場合、その名前からその実装形式を考えることができます。泡立ちというと、水中を泳ぐ小魚が小さな泡を連ねて水面に浮かび上がってくる様子をまず思い浮かべます。実はバブル選別法はバブルをはじくのと同じで、一度に1つずつ吐き出すだけで、次々と連続的に吐き出します。バブル ソート アルゴリズムの中心的な考え方は、2 つの隣接する数値を比較し、サイズ要件に従って位置を交換することです。 2 つの要素からなる最も単純な配列から始めて、そこから推論を導き出しましょう。配列「int array = {8, 0};」内に要素が 2 つだけあるとします。並べ替える際には、どの要素が大きいか、どの要素が小さいかが一度の判断で済みますので、小さい順に並べるとすると、並べた結果は「array = {0, 8};」となるはずです。 3 つの要素を持つ配列を見てみましょう。配列「int array = {8, 0, 1};」内に要素が 2 つだけあるとします。最初の比較では、配列は「array = {0, 1, 8};」であると結論付けることができ、配列の並べ替えを完了するには 1 回の比較のみが必要です。ただし、配列が要素の位置を変更する場合 (つまり、「int array = {8, 1, 0};」)、もう一度見てみましょう。要素の最初のペア比較は、「array = {1, 0,」になります。 8} ;"、したがって、この極端な状況に遭遇した場合、バブルメソッドは 1 回の比較では並べ替えを完了できず、2 回目の比較を実行する必要があります。最後に、2 回目の比較で、"array = {0, 1, 8}; "要素が 4 つの場合の配列のソートを見てみましょう。今回は極端な例として、大から小に並べられた配列を、小から大に並べた配列に変更します。配列は「int array = {9, 8, 1, 0};」です。このとき、隣接する 2 つの要素の最初の比較では「array = {8, 1, 0, 9};」が得られ、隣接する要素の 2 回目の比較では「array = {1, 0, 8, 9}」が得られます。 ;" の場合、3 番目のペア比較では "array = {0, 1, 8, 9};" が得られます。上記の分析に基づいて、配列に並べ替える必要がある n 個の要素がある場合、極端な場合の並べ替えは n-1 回である必要があることがわかります。具体的な仕分け手順は以下の通りです。

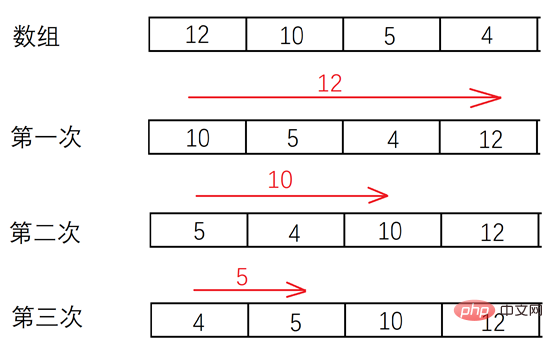
バブルソートプロセス
したがって、上記の分析に基づいて、次のようにコードを書くことができます。 。

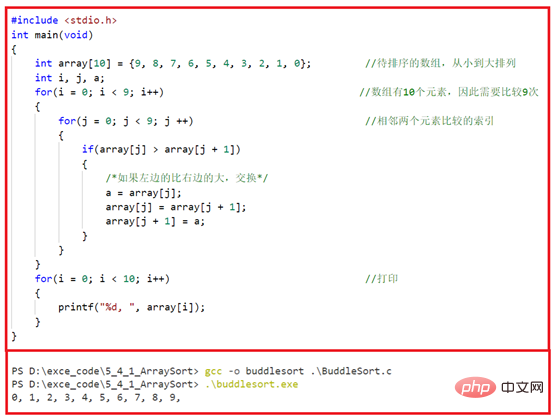
次に、図 5-4-3 に示すように、各ステップで隣接する 2 つの要素を比較するプロセスを出力するようにプログラムを変更します。 。より大きな要素が、交換 (昇順または降順に配置) によってシーケンスの先頭にゆっくりと「浮遊」することがわかります。これは、水中の小さな金魚が吐き出してゆっくりと浮上する一連の泡のように、そのためこの名前が付けられています。 "バブルソート"。

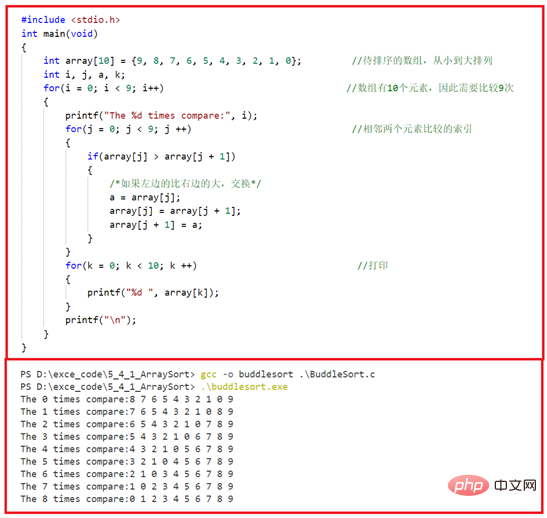
選択ソート方法

上の図では、最初の走査比較を使用して最小の要素を選択します配列の左端に配置されているので、次に行う必要があるのは、残りの 9 つの要素を一度に比較し、最小値を見つけて、それを 0 の右側に置くことなどです。選択ソート手順を次の図に示します。

#バブルソートのシングルステップ印刷選択ソート選択ソート、一般に「弾丸を噛むソート」として知られています。もちろん、この「弾丸を噛むソート」は私が付けた名前です。これは、これが最も直観的なソート方法であり、「暴力的な美学」という 4 つの言葉を完璧に解釈しているためです。選択の並べ替えを理解するには、まず、小学校の体育の授業で教師がチームをどのように配置するかを想像してください。まず、教師が一番身長が低いと思う生徒をランダムに選んでリーダーにさせ、その生徒と順番に他の生徒を比べて、その生徒の方が身長が高ければその生徒の後ろに、その生徒が背が低ければその生徒の後ろに配置されます。彼は前に配置され、次に 2 番目の者を目視で検査し、以下同様に続きます。もちろん、上記の文章は体育教師の内面を述べたものです。配列をソートするときに、この方法を使用することもできます。まず前衛を指定します。小さいものから大きいものへ並べる場合、最初の要素が配列内の最小の要素であると仮定し、それを残りの要素とそれぞれ比較します。小さいことが判明した場合は、この方法では、配列全体を走査し、最初の要素の位置に最小の要素を配置するだけで済みます。次のように。並べ替えを選択し、走査比較を実行します

#バブルソート方法

以上がJava 言語を使用してバブル ソートおよび選択ソート アルゴリズムを実装するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。