
Union-find: 結合されていないセットのマージやクエリの問題を解決するために使用されるツリー データ構造。例: n 個の村があり、2 つの村を接続する 2 つの村の間に接続道路があるかどうかをクエリします。
2 つのコア:
検索: 要素が配置されているセットを検索します
マージ (ユニオン): 2 つの要素のセットを 1 つのセットにマージします
##2. 実装に最適化可能
マージの時間計算量 (Union): O(logn) は O(a(n) )) a(n)抽象クラスの作成 Union Find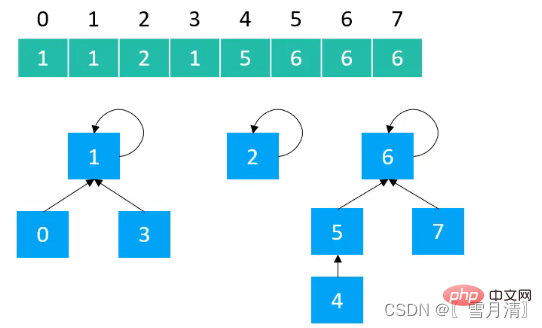
public abstract class UnionFind {
int[] parents;
/**
* 初始化并查集
* @param capacity
*/
public UnionFind(int capacity){
if(capacity < 0) {
throw new IllegalArgumentException("capacity must be >=0");
}
//初始时每一个元素父节点(根结点)是自己
parents = new int[capacity];
for(int i = 0; i < parents.length;i++) {
parents[i] = i;
}
}
/**
* 检查v1 v2 是否属于同一个集合
*/
public boolean isSame(int v1,int v2) {
return find(v1) == find(v2);
}
/**
* 查找v所属的集合 (根节点)
*/
public abstract int find(int v);
/**
* 合并v1 v2 所属的集合
*/
public abstract void union(int v1, int v2);
// 范围检查
public void rangeCheck(int v) {
if(v<0 || v > parents.length)
throw new IllegalArgumentException("v is out of capacity");
}
}public class UnionFind_QF extends UnionFind {
public UnionFind_QF(int capacity) {
super(capacity);
}
// 查
@Override
public int find(int v) {
rangeCheck(v);
return parents[v];
}
// 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
// 查找v1 v2 的父(根)节点
int p1= find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
for(int i = 0; i< parents.length; i++) {
if(parents[i] == p1) {
parents[i] = p2;
}
}
}
}2.2 迅速なユニオンの実装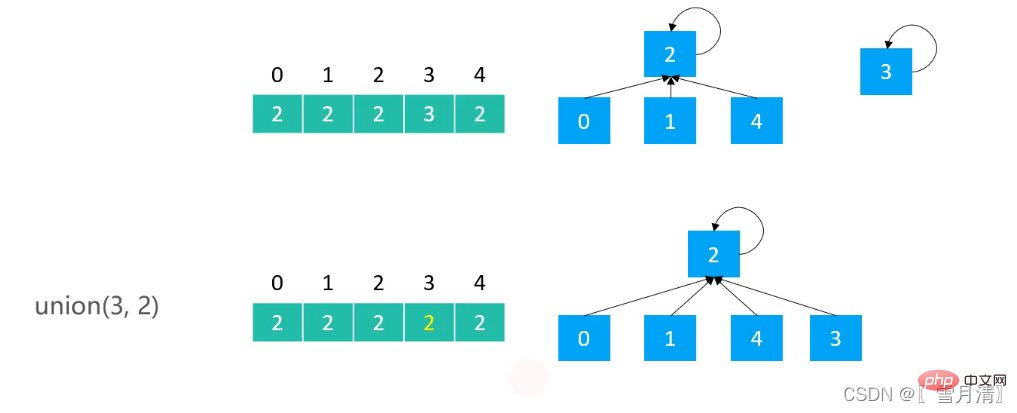
public class UnionFind_QU extends UnionFind {
public UnionFind_QU(int capacity) {
super(capacity);
}
//查某一个元素的根节点
@Override
public int find(int v) {
//检查下标是否越界
rangeCheck(v);
// 一直循环查找节点的根节点
while (v != parents[v]) {
v = parents[v];
}
return v;
}
//V1 并到 v2 中
@Override
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
parents[p1] = p2;
}
}3. 最適化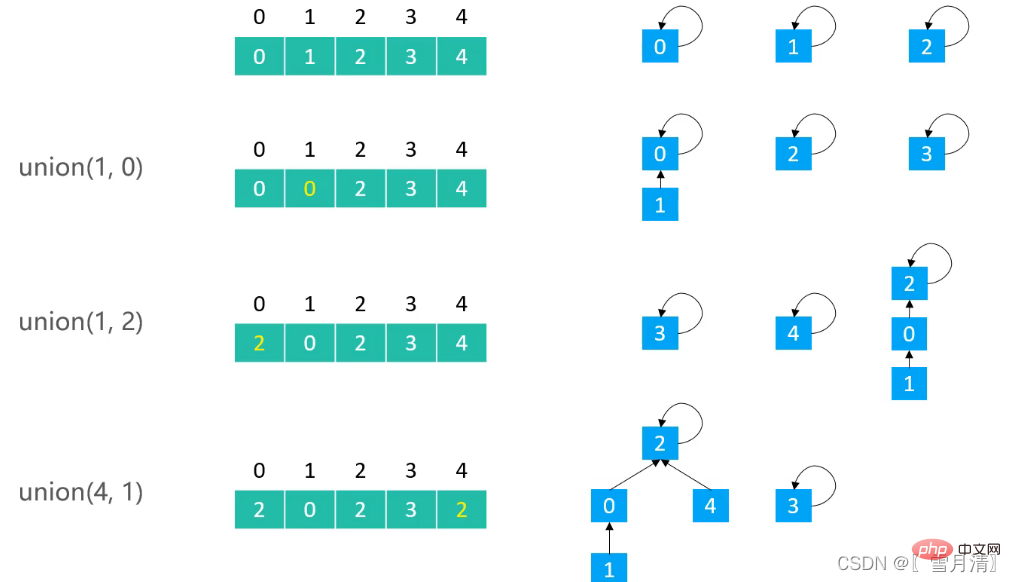
最適化のアイデアには 2 つあります: ランクの最適化とサイズの最適化 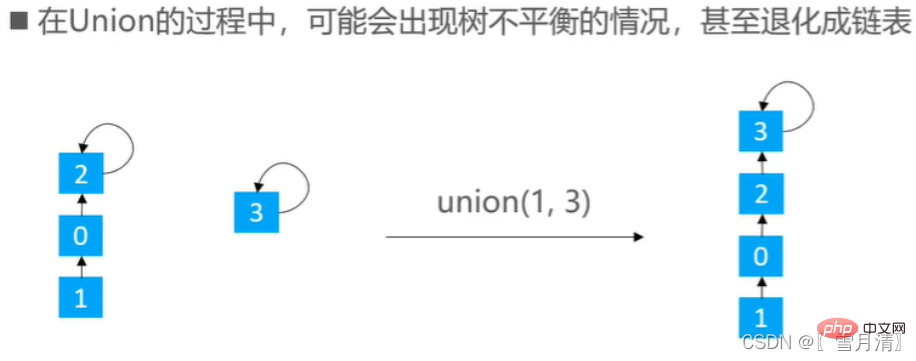
public class UniondFind_QU_S extends UnionFind{
// 创建sizes 数组记录 以元素(下标)为根结点的元素(节点)个数
private int[] sizes;
public UniondFind_QU_S(int capacity) {
super(capacity);
sizes = new int[capacity];
//初始都为 1
for(int i = 0;i < sizes.length;i++) {
sizes[i] = 1;
}
}
@Override
public int find(int v) {
rangeCheck(v);
while (v != parents[v]) {
v = parents[v];
}
return v;
}
@Override
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上,并且更新p2为根结点的元素个数
if(sizes[p1] < sizes[p2]) {
parents[p1] = p2;
sizes[p2] += sizes[p1];
// 反之 则p2 并到 p1 上,更新p1为根结点的元素个数
}else {
parents[p2] = p1;
sizes[p1] += sizes[p2];
}
}
}public class UnionFind_QU_R extends UnionFind_QU {
// 创建rank数组 ranks[i] 代表以i为根节点的树的高度
private int[] ranks;
public UnionFind_QU_R(int capacity) {
super(capacity);
ranks = new int[capacity];
for(int i = 0;i < ranks.length;i++) {
ranks[i] = 1;
}
}
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
// p1 并到 p2 上 p2为根 树的高度不变
if(ranks[p1] < ranks[p2]) {
parents[p1] = p2;
// p2 并到 p1 上 p1为根 树的高度不变
} else if(ranks[p1] > ranks[p2]) {
parents[p2] = p1;
}else {
// 高度相同 p1 并到 p2上,p2为根 树的高度+1
parents[p1] = p2;
ranks[p2] += 1;
}
}
}/**
* Quick Union -基于rank的优化 -路径压缩
*
*/
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
public UnionFind_QU_R_PC(int capacity) {
super(capacity);
}
@Override
public int find(int v) {
rangeCheck(v);
if(parents[v] != v) {
//递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
parents[v] = find(parents[v]);
}
return parents[v];
}
}ツリーの高さは減らすことができますが、実装コストが若干高くなります 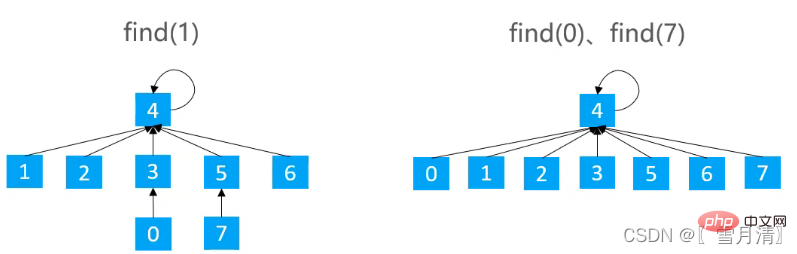
/**
* Quick Union -基于rank的优化 -路径分裂
*
*/
public class UnionFind_QU_R_PS extends UnionFind_QU_R {
public UnionFind_QU_R_PS(int capacity) {
super(capacity);
}
@Override
public int find(int v) {
rangeCheck(v);
while(v != parents[v]) {
int p = parents[v];
parents[v] = parents[parents[v]];
v = p;
}
return v;
}
}3.2.3 パスを半分にします (パスの半分化) 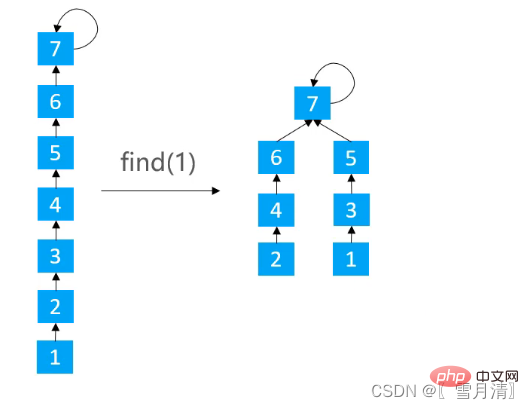
/**
* Quick Union -基于rank的优化 -路径减半
*
*/
public class UnionFind_QU_R_PH extends UnionFind_QU_R {
public UnionFind_QU_R_PH(int capacity) {
super(capacity);
}
public int find(int v) {
rangeCheck(v);
while(v != parents[v]) {
parents[v] = parents[parents[v]];
v = parents[v];
}
return v;
}
}クイック ユニオンを使用して、ランクに基づいてパスの分割またはパスの半分化を最適化します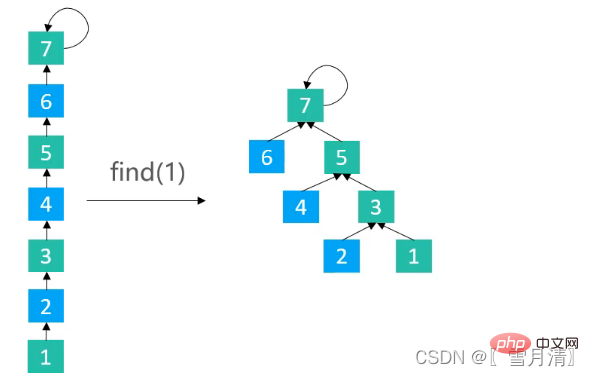
以上がJavaでのunion-findの分析例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。