
この記事は、javascript に関する関連知識を提供します。主に JavaScript バイナリ ツリーとさまざまなトラバーサル アルゴリズムの詳細を紹介します。この記事では、このトピックに関する詳細な紹介が提供されており、一定の参考価値があります。必要な方は参考にしていただければ幸いです。

[関連する推奨事項: JavaScript ビデオ チュートリアル 、Web フロントエンド ]
バイナリ ツリーは、次の図に示すように、各ノードが最大 2 つの子ノードのみを持つことができるツリーです。
#バイナリ ツリーには次の特徴があります: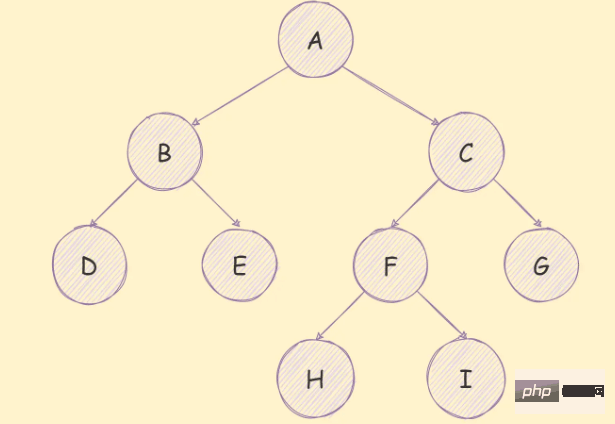
i には 2^(i-1)
ノードしかありません。このバイナリ ツリーの深さが k の場合、バイナリ ツリーには最大 2^k-1空ではないバイナリ ツリーで、葉ノードの数を表すのに n0 を使用し、次数 2 の非葉ノードの数を n2 を満たします。 下図のように
## 通常のバイナリの特性を満たすことに加えてツリーと同様に、完全なバイナリ ツリーには次の機能もあります。 特徴:
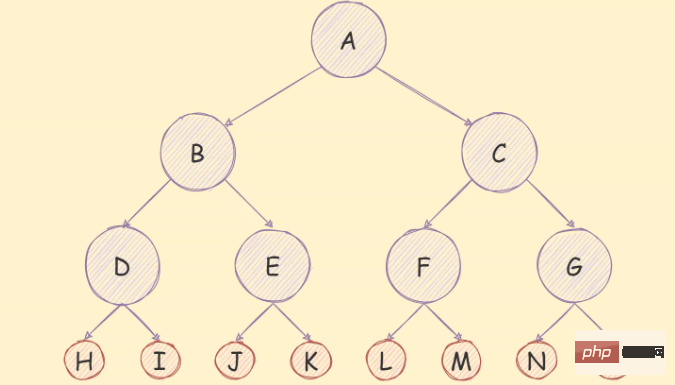
n 番目のレベルには 2^(n- 1)
ノード;k の深さの完全なバイナリ ツリーには 2^k-1 ノードが必要で、リーフ ノードの数はn ノードを持つ完全なバイナリ ツリーの深さは log_2^(n 1) です。 完全なバイナリ ツリー
バイナリ ツリーのストレージ
バイナリ ツリーのストレージ 一般的な方法は 2 つあり、1 つは配列ストレージ 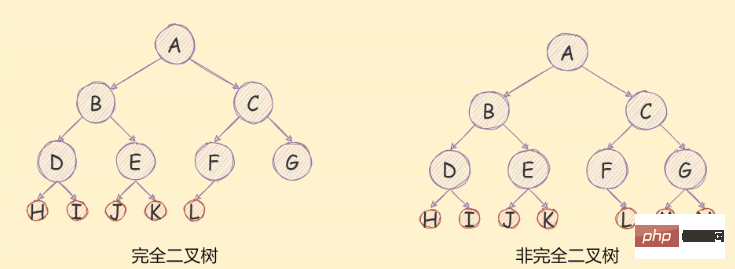 を使用する方法、もう 1 つはリンク リスト ストレージを使用する方法です。
を使用する方法、もう 1 つはリンク リスト ストレージを使用する方法です。
配列を使用してバイナリ ツリーを保存します。完全なバイナリ ツリーが見つかった場合、保存順序は、図に示すように、上から下、左から右の順になります。次の図:
下に示すように、不完全なバイナリ ツリーの場合:
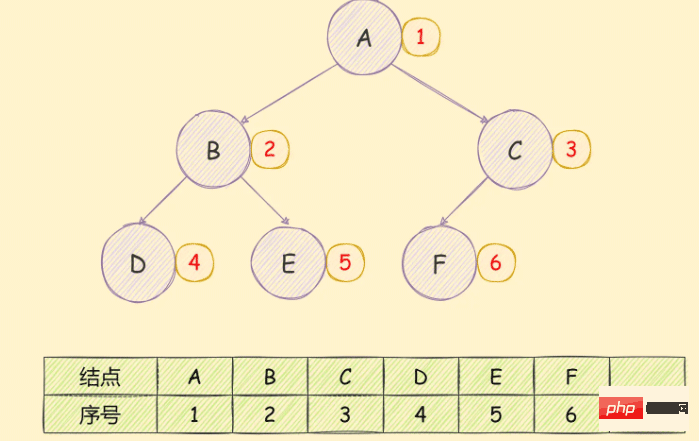
##必須 次の図に示すように、まず完全なバイナリ ツリーに変換してから保存します。ストレージスペースの無駄がはっきりわかります。
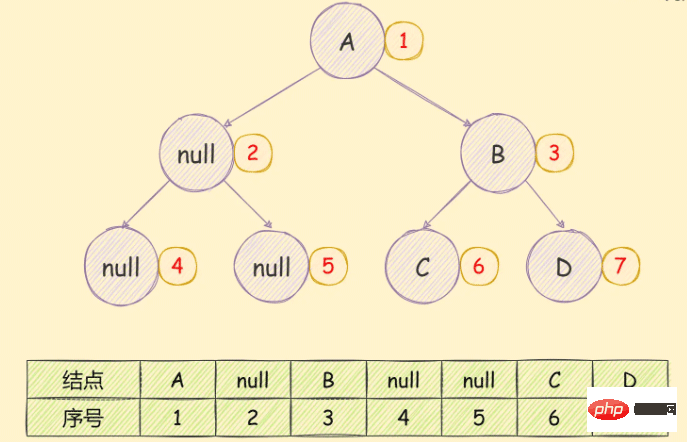
リンク リスト ストレージ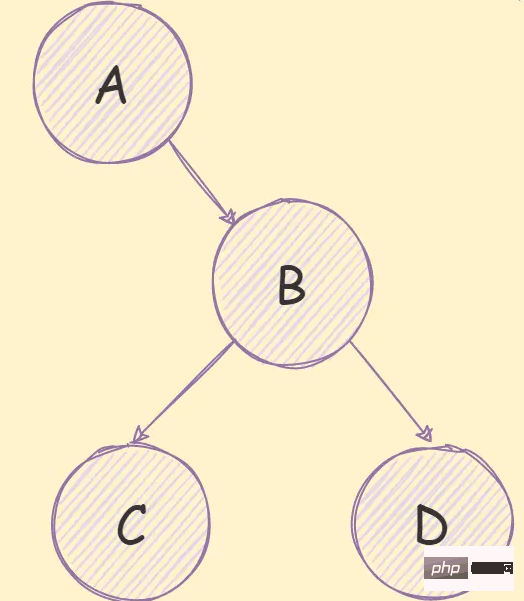
バイナリ ツリーに関連するアルゴリズム
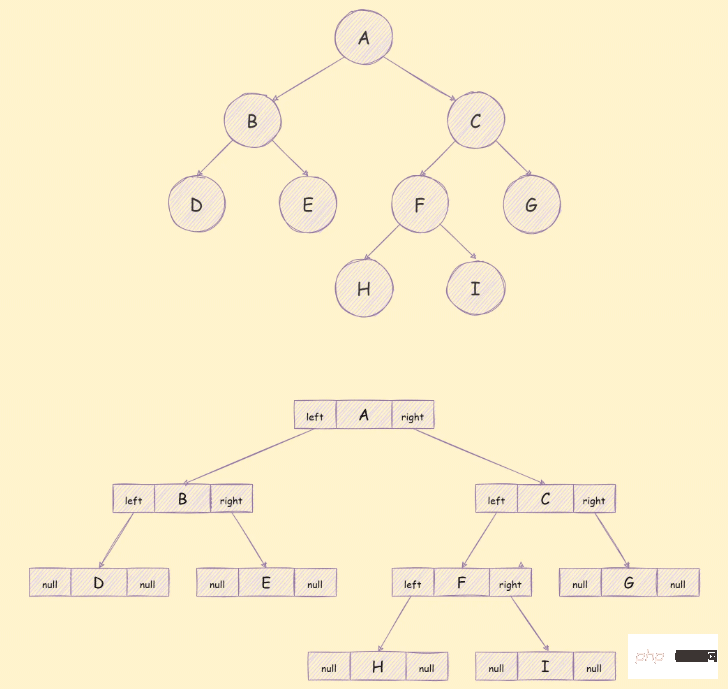
次のアルゴリズムで走査に使用されるツリーは次のとおりです:
// tree.js
const bt = {
val: 'A',
left: {
val: 'B',
left: { val: 'D', left: null, right: null },
right: { val: 'E', left: null, right: null },
},
right: {
val: 'C',
left: {
val: 'F',
left: { val: 'H', left: null, right: null },
right: { val: 'I', left: null, right: null },
},
right: { val: 'G', left: null, right: null },
},
}
module.exports = btバイナリ ツリーの深さ優先トラバーサルは、ツリーの深さ優先トラバーサルと同じ考え方を持っています。その考え方は次のとおりです:
left にアクセスします。
ルート ノードにアクセスするには2 番目と 3 番目のステップを繰り返します
const bt = {
val: 'A',
left: {
val: 'B',
left: { val: 'D', left: null, right: null },
right: { val: 'E', left: null, right: null },
},
right: {
val: 'C',
left: {
val: 'F',
left: { val: 'H', left: null, right: null },
right: { val: 'I', left: null, right: null },
},
right: { val: 'G', left: null, right: null },
},
}
function dfs(root) {
if (!root) return
console.log(root.val)
root.left && dfs(root.left)
root.right && dfs(root.right)
}
dfs(bt)
/** 结果
A B D E C F H I G
*/幅優先トラバーサル## にアクセスします# キューの先頭にある left と
rightキューが空になるまで手順 2 と 3 を繰り返します
function bfs(root) {
if (!root) return
const queue = [root]
while (queue.length) {
const node = queue.shift()
console.log(node.val)
node.left && queue.push(node.left)
node.right && queue.push(node.right)
}
}
bfs(bt)
/** 结果
A B C D E F G H I
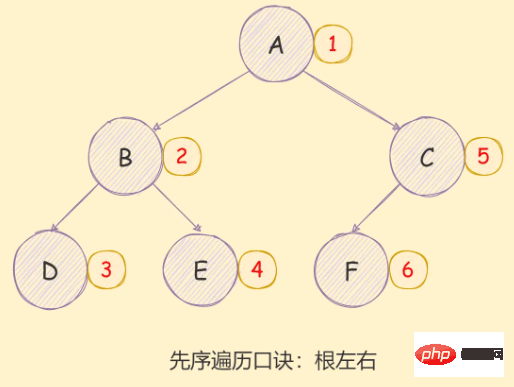
*/バイナリの pre-order traversal の実装アイデアツリーは次のとおりです: - 访问根节点;
- 对当前节点的左子树进行先序遍历;
- 对当前节点的右子树进行先序遍历;
如下图所示:
递归方式实现如下:
const bt = require('./tree')
function preorder(root) {
if (!root) return
console.log(root.val)
preorder(root.left)
preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/ログイン後にコピー迭代方式实现如下:
// 非递归版
function preorder(root) {
if (!root) return
// 定义一个栈,用于存储数据
const stack = [root]
while (stack.length) {
const node = stack.pop()
console.log(node.val)
/* 由于栈存在先入后出的特性,所以需要先入右子树才能保证先出左子树 */
node.right && stack.push(node.right)
node.left && stack.push(node.left)
}
}
preorder(bt)
/** 结果
A B D E C F H I G
*/ログイン後にコピー中序遍历
二叉树的中序遍历实现思想如下:
- 对当前节点的左子树进行中序遍历;
- 访问根节点;
- 对当前节点的右子树进行中序遍历;
如下图所示:
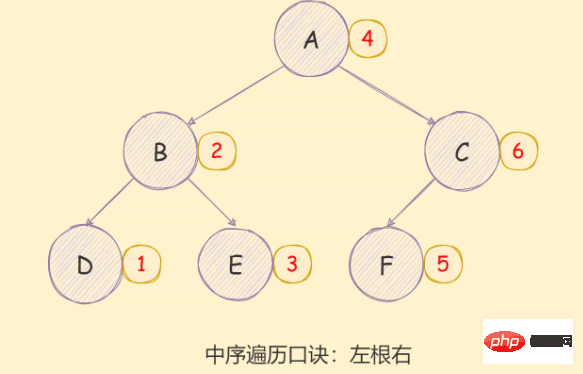
递归方式实现如下:
const bt = require('./tree')
// 递归版
function inorder(root) {
if (!root) return
inorder(root.left)
console.log(root.val)
inorder(root.right)
}
inorder(bt)
/** 结果
D B E A H F I C G
*/ログイン後にコピー迭代方式实现如下:
// 非递归版
function inorder(root) {
if (!root) return
const stack = []
// 定义一个指针
let p = root
// 如果栈中有数据或者p不是null,则继续遍历
while (stack.length || p) {
// 如果p存在则一致将p入栈并移动指针
while (p) {
// 将 p 入栈,并以移动指针
stack.push(p)
p = p.left
}
const node = stack.pop()
console.log(node.val)
p = node.right
}
}
inorder(bt)
/** 结果
D B E A H F I C G
*/ログイン後にコピー后序遍历
二叉树的后序遍历实现思想如下:
- 对当前节点的左子树进行后序遍历;
- 对当前节点的右子树进行后序遍历;
- 访问根节点;
如下图所示:
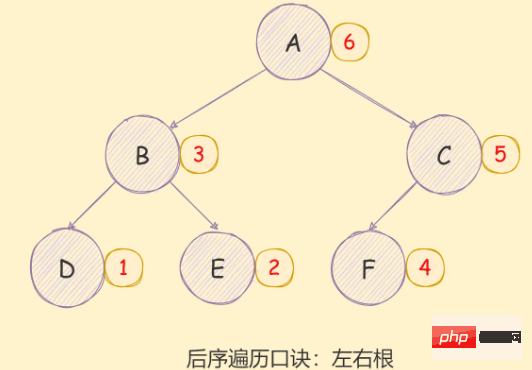
递归方式实现如下:
const bt = require('./tree')
// 递归版
function postorder(root) {
if (!root) return
postorder(root.left)
postorder(root.right)
console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/ログイン後にコピー迭代方式实现如下:
// 非递归版
function postorder(root) {
if (!root) return
const outputStack = []
const stack = [root]
while (stack.length) {
const node = stack.pop()
outputStack.push(node)
// 这里先入left需要保证left后出,在stack中后出,就是在outputStack栈中先出
node.left && stack.push(node.left)
node.right && stack.push(node.right)
}
while (outputStack.length) {
const node = outputStack.pop()
console.log(node.val)
}
}
postorder(bt)
/** 结果
D E B H I F G C A
*/ログイン後にコピー
【相关推荐:javascript视频教程、web前端】
以上がJavaScript バイナリ ツリーとさまざまなトラバーサル アルゴリズムの詳細な紹介の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。