線形時間の選択-よくある問題-php.cn

線形時間の選択

定義: 線形シーケンス内の n 個の要素と整数 k (1≤k≤n) が与えられた場合、これらの n 要素の中で k 番目に小さい要素を見つける必要があります。要素。

(1) 一部の特殊なケースでは、選択問題を解決するための線形時間アルゴリズムを設計するのが簡単です。たとえば、最大の要素または最小の要素を選択する場合、明らかに O(n) 時間で実行できます。 (1 つだけ比較)

(2) 一般的な選択問題、特に中央値の選択問題は、最小 (大きい) 要素よりも難しいようです。しかし実際には、漸近順序という意味では、それらは同じです。 O(n) 時間で実行することもできます。

線形時間選択方法 1: randomizedSelect

アイデア: 配列全体をソートするのではなく、選択したソート (高速)

時間計算量:

(1) 最悪の場合、アルゴリズムrandomizedSelectにはO(n^2)の計算時間が必要です

eg最小の要素を見つける必要がありますが、Partition 関数で分割するたびに得られる位置は常に非常に大きい (n に近い) (つまり、常に最大の要素で分割されます)

( 2) しかし、それは可能です。アルゴリズム randomizedSelect は、平均 O(n) 時間で n 個の入力要素の中から k 番目に小さい要素を見つけることができることが証明されています。

コードは次のとおりです:

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int Partition(int a[],int p,int r){
    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int RandomizedPartition(int a[],int p,int r){
    int i=rand()%(r-p)+p;
    swap(a[p],a[i]);
    return Partition(a,p,r);
}

int RandomizedSelect(int a[],int p,int r,int k){
    if(p==r)return a[p];
    int i=RandomizedPartition(a,p,r);//返回基准元素的位置
    int j=i-p+1;//表示基准元素及其左边一共多少个元素
    if(k<=j)RandomizedSelect(a,p,i,k);
    else RandomizedSelect(a,i+1,r,k-j);
}
int main(){
    int a[10]={3,1,7,6,5,9,8,2,0,4};
    int x;
    while(scanf("%d",&x)!=EOF){
        int ans=RandomizedSelect(a,0,9,x);
        printf("%d\n",ans);
    }
}

ログイン後にコピー

線形時間の選択方法 2:

線形時間でを ## 見つけられる場合 #分割ベンチマーク、このベンチマークに従って分割された 2 つの部分配列の長さが元の配列の長さの少なくとも ε 倍 (0<ε<1 は特定の正の定数) になるように、最悪の場合に使用できます。選択タスクが完了するまでに O(n) 時間がかかります。

たとえば、ε=9/10 の場合、アルゴリズムの再帰呼び出しによって生成される部分配列の長さは、少なくとも 1/10 短縮されます。したがって、最悪の場合、アルゴリズムに必要な計算時間 T(n) は、再帰式 T(n) ≦ T(9n/10) O(n) を満たすことになります。これから、T(n)=O(n) が得られます。

先生がこのことについて話したとき、私はそれを非常に鮮明に覚えています。先生は、

determine ではなく find であると強調していました。「見つける」とは中央値を見つけることを意味します値、および以前のクイックソートなどは、値の位置を決定する、つまり参照要素を正しい位置に配置するためのものでした。

手順:

(1) n 個の入力要素を n/5 (切り上げ) のグループに分割します。グループには 5 つの要素が含まれており、5 つの要素を含まないグループは最大 1 つ存在する可能性があります。任意の並べ替えアルゴリズムを使用して各グループの要素を並べ替え、各グループの中央値、合計 n/5 (切り上げ) を取得します。

(2) select を再帰的に呼び出して、これらの n/5 (切り上げ) 要素の中央値を見つけます。 n/5 (切り上げ) が偶数の場合、その 2 つの中央値のうち大きい方を見つけます。この要素を分割の基礎として使用します。

分割戦略の概略図:

白い点: 各グループの中央値、点 x: 中央値の中央値

線形時間の選択

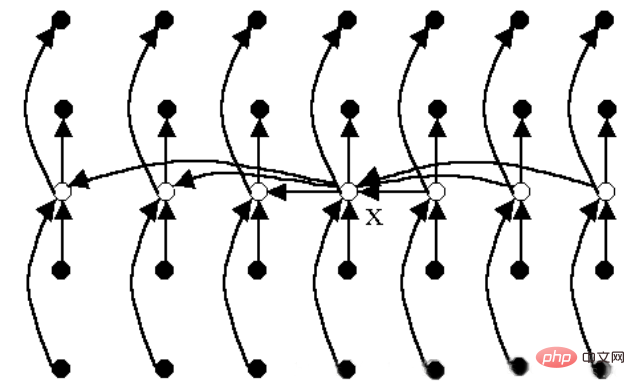
例:

昇順で、次の 18 番目の要素を見つけます。 29 要素: 8,31,60,33,17,4,51,57,49,35,11,43,37,3,13,52,6,19,25,32,

54,16,5,41,7,23,22,46,29.
(1) 最初の 25 要素を 5 つのグループ (=floor(29/5)) に分割します: (8,31,60, 33) ,17)、(4,51,57,49,35)、(11,43,37,3,13)、(52,6,19,25,32)、(54,16,5,41,7) );
(2) 各グループの中央値要素を抽出してセット {31,49,13,25,16} を形成します。;
(3) アルゴリズムを再帰的に使用してセットの中央値を見つけます。 m=25;
(4) m=25 に従って、29 個の要素を 3 つの部分配列に分割します (元の順序で)
P={8,17,4,11, 3,13,6 ,19 ,16,5,7,23,22}
Q={25}

R={31,60,33,51,57,49,35,43,37,52, 32, 54,41,46,29}

(5) |P|=13,|Q|=1,k=18 なので、P と Q を諦めて k=18-13-1 = とします。 4、このアルゴリズムを R に対して再帰的に実行します;

(6) R を 3 つの (floor(15/5)) グループに分割します: {31,60,33,51,57},{49,35,43 ,37, 52},{32,54,41,46,29}
(7) これら 3 つの要素グループの中央値要素を見つけます: {51,43,41}、このセットの中央値要素は 43;
(8) 43:

{31, 33, 35,37,32, 41, 29},{43},{60, 51,57 , 49, 52, に基づいて R を 3 つのグループに分割します。 54, 46}

複雑さ:

配列の長さが n であると仮定します

n<75 の場合、アルゴリズムで使用される計算時間は一定を超えないことを選択しますconstant C1
n≥75 の場合、for ループは n/5 回実行され、そのたびに特定の定数 (固定数、つまり 5 つの中から検索!) が使用されます。中央値の中央値を見つけるために選択します。長さが元の長さの 1/5 であるため、かかった時間は T(n/5) として記録できます。分割後、得られる配列の要素数は最大 3n/4 となり、かかった時間は T(3n /4)。したがって、T(n) は次のように再帰的に表すことができます:

線形時間の選択

この再帰式の解は、T(n)=O(n)

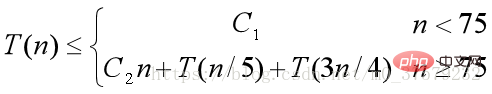
です。

上述算法将每一组的大小定为5，并选取75作为是否作递归调用的分界点（大于75使用该算法）。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn，0<ε<1。这是使T(n)=O(n)的关键之处。当然，除了5和75之外，还有其他选择。

注意：

（1）设中位数的中位数是x，比x小和比x大的元素至少3*(n-5)/10个，原因：

3*(n/5-1)*1/2

3---中位数比x小的每一组中有3个元素比x小

n/5-1---有5个数的组数

1/2---大概有1/2组的中位数比x小

（2）而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4，也就是说，长度最长为原长度的3/4。

線形時間の選択

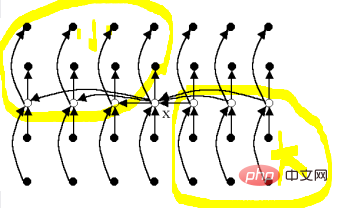
如图，划分的部分左上是肯定比x小的（大概占1/4）右下是肯定比x大的（大概占1/4）左下和右上不确定，就算这两部分同时不比x小或比x大，划分成的子区间也能至少缩短1/4!

核心代码：

Type Select(Type a[], int p, int r, int k)
{
      if (r-p<75) {
        //用某个简单排序算法对数组a[p:r]排序;
        return a[p+k-1];
        };
      for (int i=0;i<=(r-p-4)/5;i++)//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面
  
      //找中位数的中位数，r-p-4即上面所说的n-5
      Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//x是中位数的中位数
      int i=Partition(a,p,r,x),j=i-p+1;//i为快排一趟找到区间[p,r]中x应该在的位置，j为[p,i]区间的元素个数
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

ログイン後にコピー

关键的代码是：

for ( int i = 0; i<=(r-p-4)/5; i++ )//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面

ログイン後にコピー

一共(r-p+1)/5个组

注意这里i从0开始表示，为了方便交换时带入数组的下标，0-(r-p-4)/5，即一共(r-p-4)/5+1各组，即(r-p+1)/5个组

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
using namespace std;

void bubbleSort(int a[],int p,int r){
    for(int i=p;i<r;i++){
        for(int j=i+1;j<=r;j++){
            if(a[j]<a[i])swap(a[i],a[j]);
        }
    }
}

int Partition(int a[],int p,int r,int val){
    int pos;
    for(int q=p;q<=r;q++){
        if(a[q]==val){pos=q;break;}
    }
    swap(a[p],a[pos]);

    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int Select(int a[],int p,int r,int k){
    if(r-p<75){
        bubbleSort(a,p,r);
        return a[p+k-1];
    }

    for(int i=0;i<=(r-p-4)/5;i++){//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
        int s=p+5*i,t=s+4;
        for(int j=0;j<3;j++){//冒泡排序，从后开始排，结果使得后三个数是排好顺序的（递增）
            for(int n=s;n<t-j;n++){
                if(a[n]>a[n+1])swap(a[n],a[n-1]);
            }
        }
        swap(a[p+i],a[s+2]);//交换每组中的中位数到前面
    }
    //(r-p-4)/5表示组数-1，则[p,p+(r-p-4)/5]的区间长度等于组数
    int x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//求中位数的中位数
    int i=Partition(a,p,r,x),j=i-p+1;
    if(k<=j)return Select(a,p,i,k);
    else return Select(a,i+1,r,k-j);
}
int main(){
    int x;
    //数组a存了0-79
    int a[80]={3,1,7,6,5,9,8,2,0,4,
               13,11,17,16,15,19,18,12,10,14,
               23,21,27,26,25,29,28,22,20,24,
               33,31,37,36,35,39,38,32,30,34,
               43,41,47,46,45,49,48,42,40,44,
               53,51,57,56,55,59,58,52,50,54,
               63,61,67,66,65,69,68,62,60,64,
               73,71,77,76,75,79,78,72,70,74,
              };
    while(scanf("%d",&x)!=EOF){
        printf("第%d大的数是%d\n",x,Select(a,0,79,x));
    }
}

ログイン後にコピー

qwq，博主nc写错输出了，“第i小的数”

線形時間の選択