
fipy
フィックの法則とは、巨視的な混合に依存せずに物質移動現象が起こる場合の、分子拡散過程における物質移動フラックスと濃度勾配との関係を指します。フィックの法則は、1855 年にアドルフ フィックによって提案されました。

動的拡散の偏微分方程式は、フィックの第 2 法則から得られます。これを解くと濃度分布と流出曲線が得られます。
この問題に対する分析的な解決策があるかどうかはわかりませんが、数値的な解決策はより一般的な解決策です。
fipy は、まだ生きている珍しい PDE ソリューション Python パッケージで、作者は公式サンプルに基づいてこのプログラムを改変しました。
関連する推奨事項: 「Python ビデオ チュートリアル 」
質問
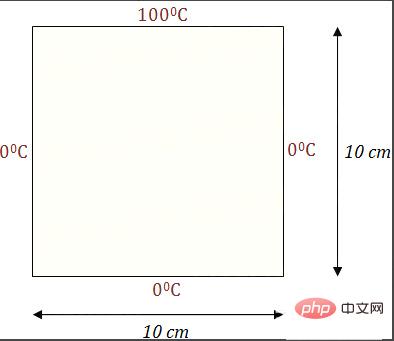
2 次元の平板、上部は 1摂氏温度 (100 もそうです、単なる係数です)、他の 3 つのエッジは摂氏 0 ℃、最初の瞬間では基板全体が摂氏 0 ℃ですが、時間が経つにつれて熱が基板に伝わり、最終的には平衡状態に達するとき、平衡状態の温度分布を知りたいだけでなく、時間の経過とともに温度がどのように変化するかも知りたいと考えています。熱の伝わり方は微分方程式で表され、単純に温度が最も早く下がる方向に熱が伝わると理解できます。
式の右側は温度の勾配、左側は温度の時間変化です。
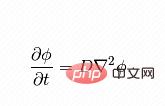
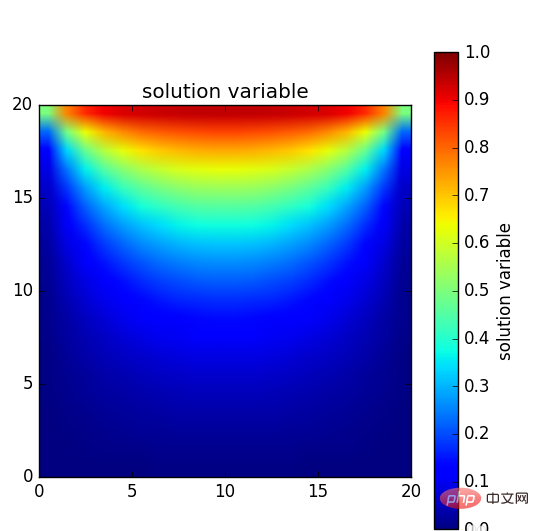
最後に、ボード全体の温度分布を大まかに示します
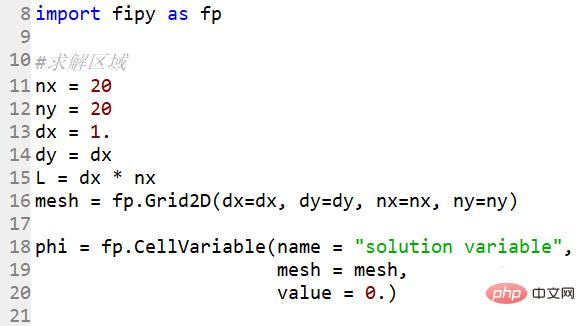
インポートする必要があるパッケージは 1 つだけです
import fipy as fp
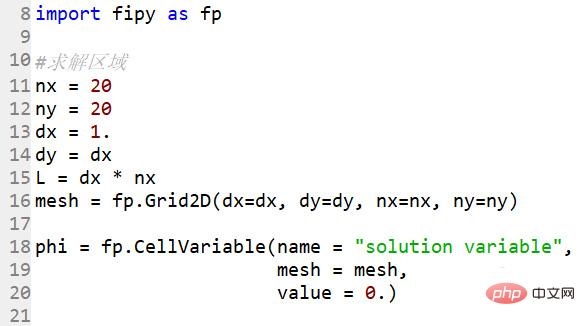
解の領域、20*20 のグリッド点を決定します
#解の領域 nx = 20ny = 20dx = 1.dy = dxL = dx * nxmesh = fp.Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)
phi = fp.CellVariable(name = "ソリューション変数", メッシュ =
境界条件の確立
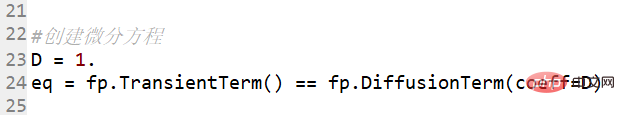
図面の作成

解決策

アニメーション画像を取得できるコマンドラインで実行することをお勧めします。ipython には最後の画像のみがあります。
 スパイダーの ipython には最後の画像しかありません
スパイダーの ipython には最後の画像しかありません
以上がPython は偏微分方程式を解くことができますか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。