
この記事では、スター除去ゲームの H5 実装の詳細を紹介します。困っている友達に役立つことを願っています。
「Destroy the Stars」は非常に古典的な「消去ゲーム」です。ゲームプレイは非常にシンプルです。同じ色の接続されたレンガを消去します。

1. ゲームルール
「Destroy the Stars」には複数のバージョンがありますが、「レベルポイント」を除いてルールは同じです。著者が紹介したバージョンのゲームルールは次のように構成されています:
1. カラーレンガの配布
10 x 10 のテーブル
5 色 - 赤、緑、青、黄、紫
各種類の数色のレンガはランダムに指定されます
5種類の色のレンガが10×10の間隔でランダムに配置されます
2. 消去ルール
同じ色のレンガを2つ以上つなげて消去できます。
3. スコアルール
合計除去スコア = n * n * 5
合計報酬スコア = 2000 – n * n * 20
「n」はレンガの数を表します。上記は、「合計」スコアのルールと、「単一」レンガのスコア ルールです:
レンガを削除するためのスコア = 10 * i + 5
残りのレンガの減点 = 40 * i + 20
「i」はレンガのインデックス値を表します(0から始まります)。簡単に言えば、1 つのレンガの「得点値」と「減点値」は等差数列です。
4. レベルスコア
レベルスコア = 1000 + (レベル – 1) * 2000; 「レベル」は現在のレベル番号です。
5. 合格条件
消去できるカラーブロックは存在しません
累計スコア >= 現在のレベルのスコア
上記 2 つの条件が同時に満たされた場合にのみゲームを通過できます。
2. MVC デザインパターン
著者は今回も MVC パターンを使用して「Destroy the Stars」を書きました。スター「ブリック」のデータ構造とさまざまな状態はモデルによって実装され、ゲームの中核はモデル内で完了します。ビューはモデル内の変更をマッピングし、対応する動作を実行します。その主なタスクはアニメーションを表示することです。 ; ユーザーとゲーム間の対話はモデル コントロールによって実装されます。
論理的な計画の観点から見ると、モデルは非常に重いですが、ビューとコントロールは非常に軽いですが、コードの観点から見ると、モデルとコントロールは比較的軽いです。
3. モデル
10 x 10 テーブルは、長さ 100 の配列を使用して、ゲームのスター「レンガ」を完全にマップします。
[ R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P, R, R, G, G, B, B, Y, Y, P, P ]
R – 赤、G – 緑、B – 青、Y – 黄、P – 紫。モデルの中心的なタスクは次の 4 つです:
レンガの壁を生成する
レンガを削除する (レンガ ポイントを生成する)
レンガの壁を統合する
残留レンガを除去する (ボーナス ポイントを生成する)
3.1 レンガの壁を生成する
レンガ壁は次の 2 つのステップで生成されます:
カラーレンガの数の割り当て
散らばったカラーレンガを構築する
理論的には、100 個のグリッドを 5 種類の色に均等に分割できますが、著者がプレイした「Destroy the Stars」戦略も使用しません。いくつかの「Destroy Stars」モデルを分析すると、実際に「色付きレンガの数の差が一定の範囲内にある」という法則を見つけることができます。
伝統的な意味での均等分割を「完全均等分割」と呼ぶなら、『星の消去』の配信は平均線を上下に変動する「不完全均等分割」である。 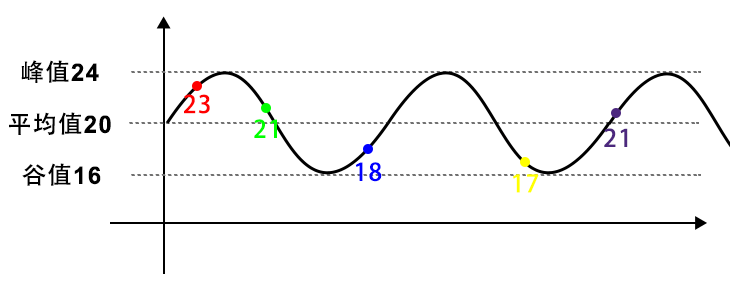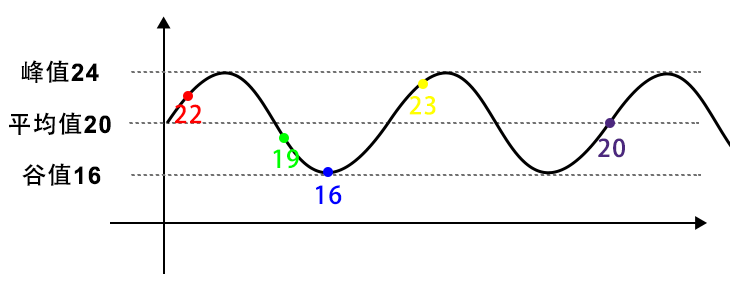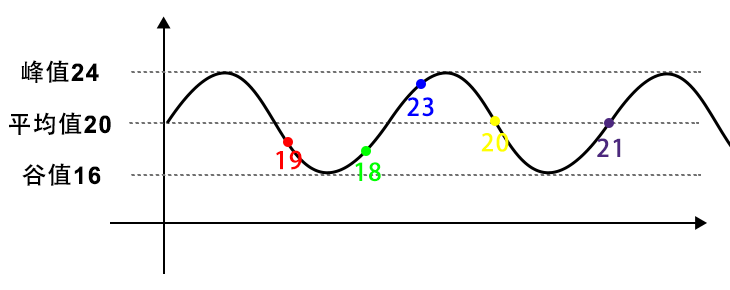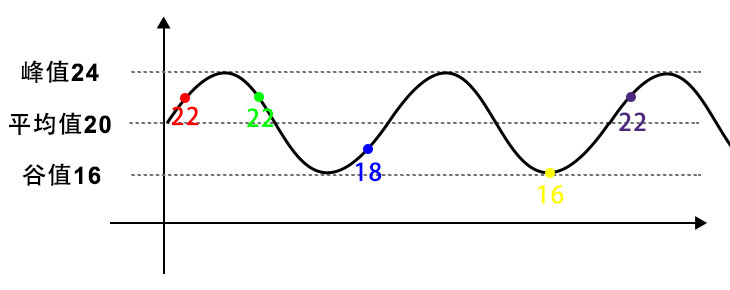
著者は上記の「不完全等化」を「変動等化」と呼んでいます。アルゴリズムの具体的な実装については「変動等化アルゴリズム」を参照してください。
「カラーレンガの分割」は実際には配列をシャッフルするプロセスであり、著者は「Fisher-Yates シャッフルアルゴリズム」を使用することを推奨しています。
以下は疑似コードの実装です:
// 波动均分色砖 waveaverage(5, 4, 4).forEach( // tiles 即色墙数组 (count, clr) => tiles.concat(generateTiles(count, clr)); ); // 打散色砖 shuffle(tiles);
3.2 レンガの削除
「レンガの削除」のルールは非常に簡単です。同じ色の隣接するレンガを削除できます。
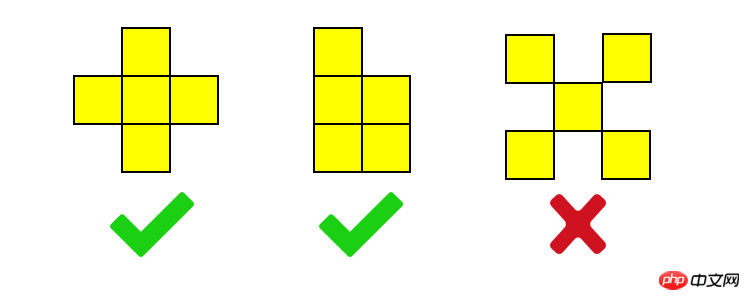
最初の 2 つの組み合わせは「同じ色で隣接しており、削除できる」に準拠しているため、削除できますが、3 番目の組み合わせは「同じ色で隣接」していますが、「接続」されていないため、削除できません。排除される。
「レンガを取り除く」際には、レンガに対応するスコアを生成するという重要なタスクがあります。 「ゲーム ルール」では、作者は対応する数式を提供しています: 「レンガを取り除くためのスコア値 = 10 * i + 5」。
「ブリック除去」アルゴリズムは次のように実装されます:
function clean(tile) {
let count = 1;
let sameTiles = searchSameTiles(tile);
if(sameTiles.length > 0) {
deleteTile(tile);
while(true) {
let nextSameTiles = [];
sameTiles.forEach(tile => {
nextSameTiles.push(...searchSameTiles(tile));
makeScore(++count * 10 + 5); // 标记当前分值
deleteTile(tile); // 删除砖块
});
// 清除完成,跳出循环
if(nextSameTiles.length === 0) break;
else {
sameTiles = nextSameTiles;
}
}
}
}クリア アルゴリズムは「再帰」を使用すると論理的に明確になりますが、「再帰」はブラウザ上で「スタック オーバーフロー」を起こしやすいため、作成者は「再帰」を使用しませんでした。 」を実行します。
3.3 レンガの壁を統合する
いくつかのレンガを削除すると、レンガの壁に穴が現れます。この時点で、壁を統合する必要があります:
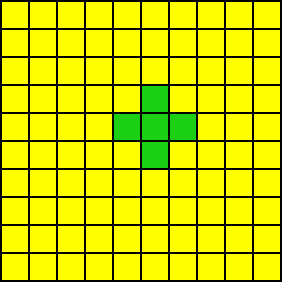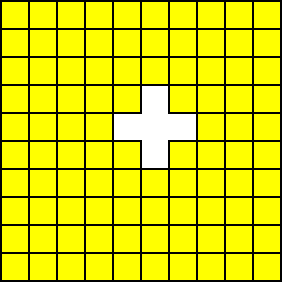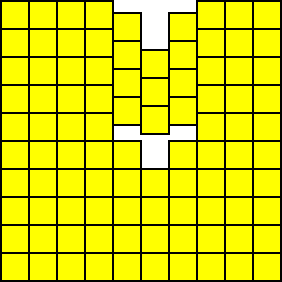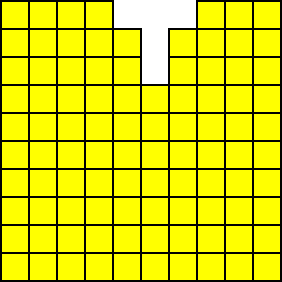
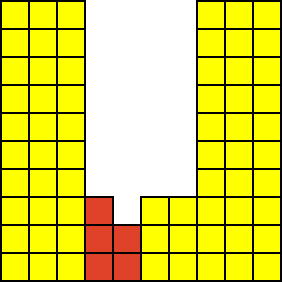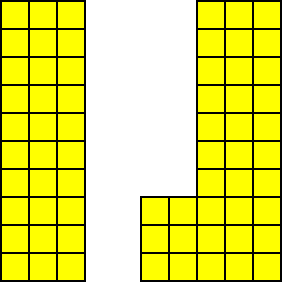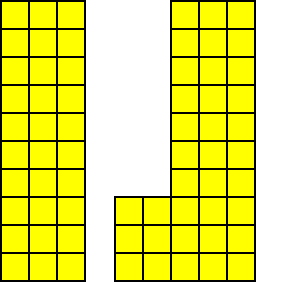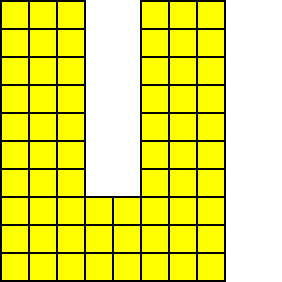
向下夯实 向左夯实
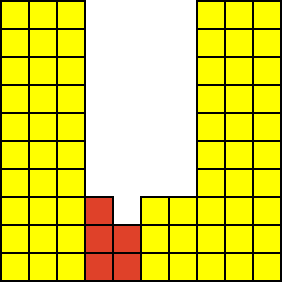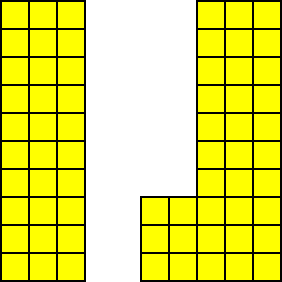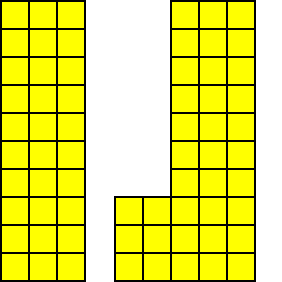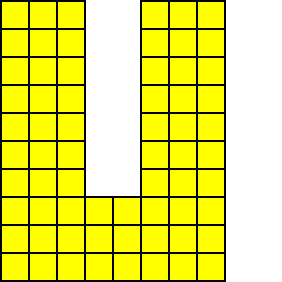
向左下夯实(先下后左)
一种快速的实现方案是,每次「消除砖块」后直接遍历砖墙数组(10×10数组)再把空洞夯实,伪代码表示如下:
for(let row = 0; row < 10; ++row) {
for(let col = 0; col < 10; ++col) {
if(isEmpty(row, col)) {
// 水平方向(向左)夯实
if(isEmptyCol(col)) {
tampRow(col);
}
// 垂直方向(向下)夯实
else {
tampCol(col);
}
break;
}
}
}But… 为了夯实一个空洞对一张大数组进行全量遍历并不是一种高效的算法。在笔者看来影响「墙体夯实」效率的因素有:
定位空洞
砖块移动(夯实)
扫描墙体数组的主要目的是「定位空洞」,但能否不扫描墙体数组直接「定位空洞」?
墙体的「空洞」是由于「消除砖块」造成的,换种说法 —— 被消除的砖块留下来的坑位就是墙体的空洞。在「消除砖块」的同时标记空洞的位置,这样就无须全量扫描墙体数组,伪代码如下:
function deleteTile(tile) {
// 标记空洞
markHollow(tile.index);
// 删除砖块逻辑
...
}在上面的夯实动图,其实可以看到它的夯实过程如下:
空洞上方的砖块向下移动
空列右侧的砖块向左移动
墙体在「夯实」过程中,它的边界是实时在变化,如果「夯实」不按真实边界进行扫描,会产生多余的空白扫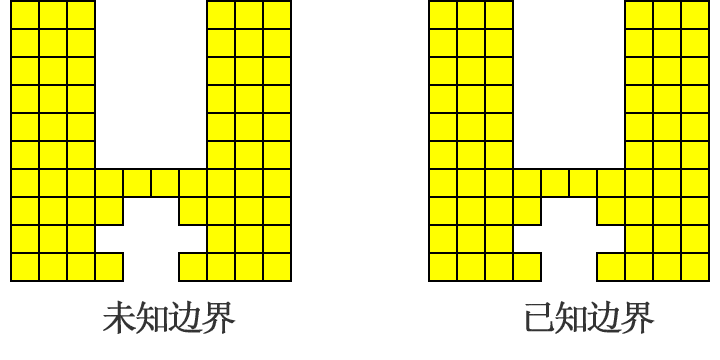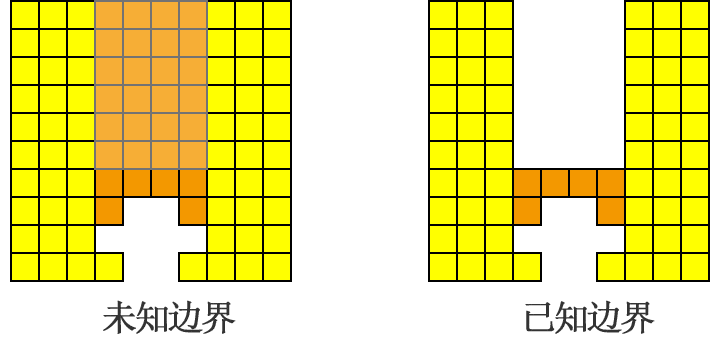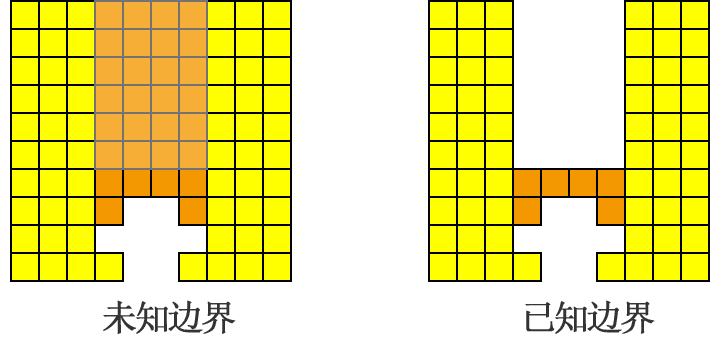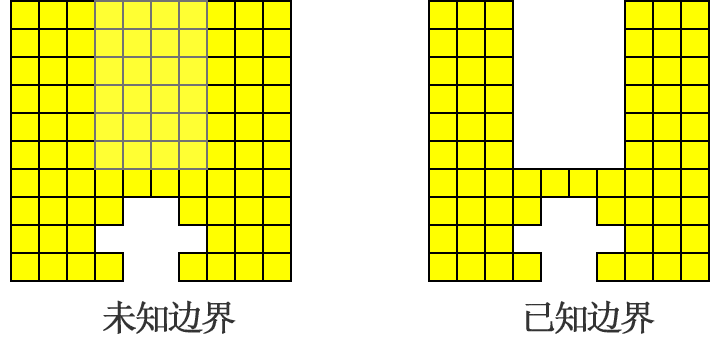
如何记录墙体的边界?
把墙体拆分成一个个单独的列,那么列最顶部的空白格片段就是墙体的「空白」,而其余非顶部的空白格片段即墙体的「空洞」。

笔者使用一组「列集合」来描述墙体的边界并记录墙体的空洞,它的模型如下:
/*
@ count - 列砖块数
@ start - 顶部行索引
@ end - 底部行索引
@ pitCount - 坑数
@ topPit - 最顶部的坑
@ bottomPit - 最底部的坑
*/
let wall = [
{count, start, end, pitCount, topPit, bottomPit},
{count, start, end, pitCount, topPit, bottomPit},
...
];这个模型可以描述墙体的三个细节:
空列
列的连续空洞
列的非连续空洞
// 空列
if(count === 0) {
...
}
// 连续空洞
else if(bottomPit - topPit + 1 === pitCount) {
...
}
// 非连续空洞
else {
...
}砖块在消除后,映射到单个列上的空洞会有两种分布形态 —— 连续与非连续。
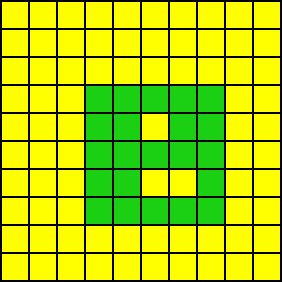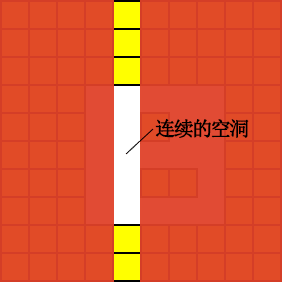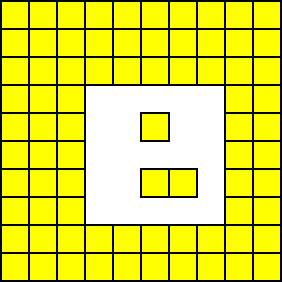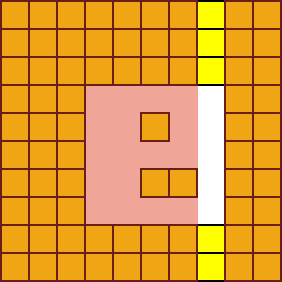
「连续空洞」与「非连续空洞」的夯实过程如下:
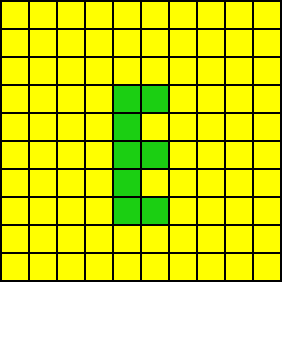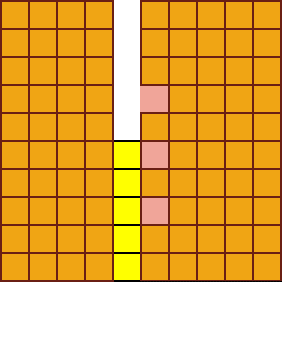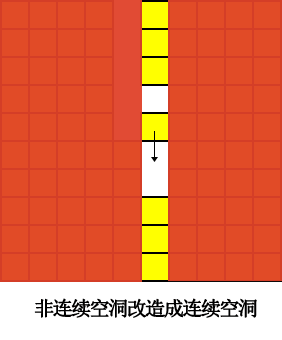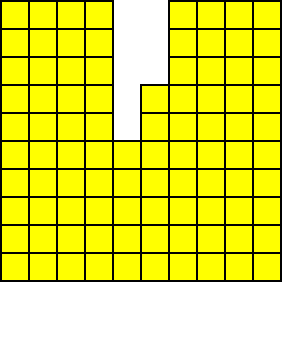
其实「空列」放大于墙体上,也会有「空洞」类似的分布形态 —— 连续与非连续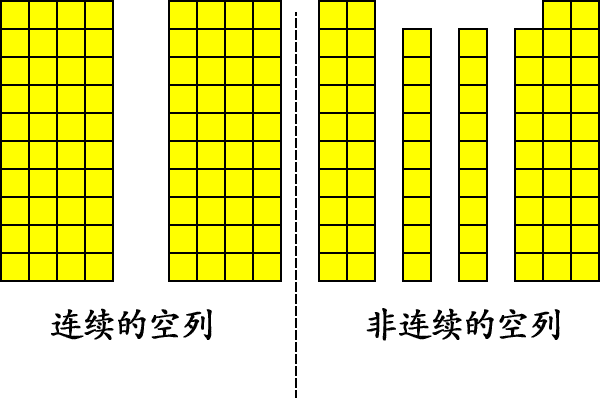
它的夯实过程与空洞类似,这里就不赘述了。
3.4 消除残砖
上一小节提到了「描述墙体的边界并记录墙体的空洞」的「列集合」,笔者是直接使用这个「列集合」来消除残砖的,伪代码如下:
function clearAll() {
let count = 0;
for(let col = 0, len = this.wall.length; col < len; ++col) {
let colInfo = this.wall[col];
for(let row = colInfo.start; row <= colInfo.end; ++row) {
let tile = this.grid[row * this.col + col];
tile.score = -20 - 40 * count++; // 标记奖励分数
tile.removed = true;
}
}
}4. View
View 主要的功能有两个:
UI 管理
映射 Model 的变化(动画)
UI 管理主要是指「界面绘制」与「资源加载管理」,这两项功能比较常见本文就直接略过了。View 的重头戏是「映射 Model 的变化」并完成对应的动画。动画是复杂的,而映射的原理是简单的,如下伪代码:
update({originIndex, index, clr, removed, score}) {
// 还没有 originIndex 或没有色值,直接不处理
if(originIndex === undefined || clr === undefined) return ;
let tile = this.tiles[originIndex];
// tile 存在,判断颜色是否一样
if(tile.clr !== clr) {
this.updateTileClr(tile, clr);
}
// 当前索引变化 ----- 表示位置也有变化
if(tile.index !== index) {
this.updateTileIndex(tile, index);
}
// 设置分数
if(tile.score !== score) {
tile.score = score;
}
if(tile.removed !== removed) {
// 移除或添加当前节点
true === removed ? this.bomb(tile) : this.area.addChild(tile.sprite);
tile.removed = removed;
}
}Model 的砖块每次数据的更改都会通知到 View 的砖块,View 会根据对应的变化做对应的动作(动画)。
5. Control
Control 要处理的事务比较多,如下:
绑定 Model & View
生成通关分值
判断通关条件
对外事件
用户交互
初始化时,Control 把 Model 的砖块单向绑定到 View 的砖块了。如下:
Object.defineProperties(model.tile, {
originIndex: {
get() {...},
set(){
...
view.update({originIndex})
}
},
index: {
get() {...},
set() {
...
view.update({index})
}
},
clr: {
get() {...},
set() {
...
view.update({clr})
}
},
removed: {
get() {...},
set() {
...
view.update({removed})
}
},
score: {
get() {...},
set() {
...
view.update({score})
}
}
})「通关分值」与「判断通关条件」这对逻辑在本文的「游戏规则」中有相关介绍,这里不再赘述。
对外事件规划如下:
| 名前 | 詳細 |
| パス |
パス |
| 一時停止 |
一時停止 |
| 再開 | 再開 |
| ゲームオーバー | ゲームオーバー |
ユーザーインタラクション API は次のように計画されています:
| name | type | deltail |
| init | method | ゲームを初期化する |
| next | メソッド | 次のレベルに入る |
| メソッドを入力 |
指定されたレベルを入力 |
|
| 一時停止 | ||
| 回復 |
||
| ゲームを破壊する |
「除去できない行列」とは、実際には最大スコアが0の行列であり、本質的には「レベル合格の条件を満たさない最大スコアの行列」です。 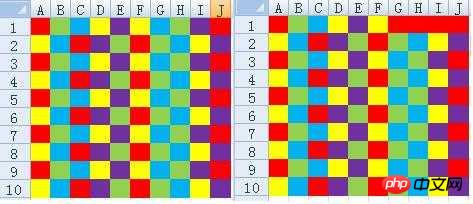
「行列」の最大スコアを求めるのは「ナップザック問題」であり、それを解くアルゴリズムは難しくありません。「再帰」を使用してすべての消去分岐を実行します。現在のマトリックスに対して 1 回だけ実行し、最高のスコアを取得します。ただし、JavaScript の「再帰」は簡単に「スタック オーバーフロー」を引き起こし、アルゴリズムの実行に失敗する可能性があります。
実際、Zhihu トピックで解決策が言及されました:
単純な推測ゲームを作成するための HTML5 Canvas API
以上がH5開発:星を破壊するゲームの実現の詳細の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。